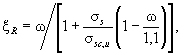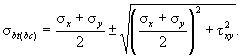|
|||||||||||||||
Все документы, представленные в каталоге, не являются их официальным изданием и предназначены исключительно для ознакомительных целей. Электронные копии этих документов могут распространяться без всяких ограничений. Вы можете размещать информацию с этого сайта на любом другом сайте.
НИИЖБ Госстроя СССР
ПОСОБИЕ
по проектированию
армоцементных
конструкций
(к СНиП 2.03.03-85)
Утверждено
приказом НИИЖБ Госстроя СССР
от 29 апреля 1986 г. № 25
Москва Стройиздат 1989
Рекомендовано к изданию решением секции теории железобетона и арматуры Научно-технического совета НИИЖБ Госстроя СССР.
Пособие по проектированию армоцементных конструкций: (к СНиП 2.03.03-85)/НИИЖБ. - М.: Стройиздат, 1989.
Изложены общие положения и расчетные требования при проектировании армоцементных конструкций. Рассмотрены виды материалов и арматура, используемые для армоцементных конструкций, а также их расчетные и нормативные характеристики. Даны примеры расчета.
Для инженерно-технических работников проектных и строительных организаций.
Табл. 17, ил. 60.
Разработано НИИЖБ Госстроя СССР (д-р техн. наук, проф. Г.К. Хайдуков - руководитель темы, канд. техн. наук, Е.К. Качановскийй - разд. 1 - 5, канд. техн. наук В.В. Фигаровский - разд. 1); при участии ЛенЗНИИЭП Госгражданстроя (кандидаты техн. наук Б.А. Миронков, С.Н. Панарин, инж. Г.М. Абраменкова - примеры), НИИСК Госстроя СССР (кандидаты техн. наук В.Д. Галич, В.П. Овчар, инж. Т.В. Борисова - примеры).
ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ
Усилия от внешних нагрузок и воздействий в поперечном сечении элемента и от предварительного напряжения
M - изгибающий момент;
N - продольная сила;
Q - поперечная сила;
P - усилие предварительного обжатия.
Характеристики материалов
Rb, Rb, ser - расчетные сопротивления мелкозернистого бетона сжатию соответственно для предельных состояний первой и второй групп;
Rbt, Rbt, ser - расчетные сопротивления мелкозернистого бетона растяжению соответственно для предельных состояний первой и второй групп;
Rsc, Rs, Rspc, Rsp - расчетные сопротивления проволочной и стержневой ненапряженной и напряженной арматуры;
Rc1 - расчетное приведенное сопротивление бетона сжатой зоны сечения;
Rm - расчетное сопротивление сеток растяжению для предельных состояний первой группы;
Rmω - расчетное сопротивление сеток растяжению при расчете сечений на поперечную силу в наклонных сечениях;
Rmc - расчетное сопротивление сеток сжатию;
Eb - начальный модуль упругости мелкозернистого бетона при сжатии и растяжении;
Em - модуль упругости сеток;
α - отношение модулей упругости сетчатой арматуры Em и бетона Eb;
Es - модуль упругости стержневой и проволочной арматуры.
Геометрические характеристики
Ab - площадь сечения бетона;
A'm, Am - площадь сечения проволок сетки в сжатой и растянутой зонах;
Ac, At - площади сечения бетона сжатой и растянутой зон соответственно;
A's, As - площади сечения ненапрягаемой стержневой арматуры на единицу ширины соответственно в сжатой и растянутой зонах;
A'sp, Asp - площади ненапрягаемой стержневой арматуры на единицу ширины соответственно в сжатой и растянутой зонах;
μm - коэффициент сетчатого армирования, определяемый как отношение площади арматуры Am к площади сечения бетона Ab;
μ's, μs, μ'sp, μsp - коэффициент армирования стержневой и проволочной сжатой, растянутой арматурой соответственно ненапрягаемой и напрягаемой;
μm, μ'm - коэффициенты армирования, приведенные к сетчатому, соответственно для растянутой и сжатой зоны;
t'f, tf - толщина соответственно сжатой и растянутой полок двутаврового сечения;
b - ширина сечения;
bfc, bf - ширина соответственно сжатой и растянутой полок двутаврового сечения;
h - высота прямоугольного, таврового или двутаврового сечения;
a', a - расстояния от равнодействующей сосредоточенной сжатой A's, A'sp и растянутой As, Asp арматуры до ближайшей грани сечения;
x - высота сжатой зоны бетона;
ξ - относительная высота сжатой зоны бетона, равная ξ = x/h;
ec - эксцентриситет продольной силы N относительно центра тяжести приведенного сечения;
l1 - расчетная длина армоцементного элемента, подвергающегося действию сжимающей продольной силы;
dm - диаметр проволок сварных, тканых и плетеных сеток;
l - пролет элемента;
r - радиус инерции поперечного сечения элемента относительно центра тяжести сечения;
ds - номинальный диаметр стержневой арматуры;
I1 - момент инерции сечения, приведенного к бетонному, относительно его центра тяжести;
Is1 - момент инерции сечения, приведенного к стальному, относительно его центра тяжести;
Ws1 - момент сопротивления растянутого волокна, приведенного к стальному;
Bf1 - жесткость сечения элемента армоцементных конструкций при кратковременном действии нагрузки;
Bf2 - жесткость сечения армоцементных конструкций при действии нагрузок, на участке, в пределах которого образуются трещины;
B'f2 - жесткость сечения элемента армоцементных конструкций при действии эксплуатационной нагрузки;
yc - расстояние до центра тяжести.
1. ОБЩИЕ УКАЗАНИЯ
ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Настоящее Пособие составлено к СНиП 2.03.03-85 «Армоцементные конструкции» и распространяется на проектирование армоцементных конструкций промышленных, гражданских и сельскохозяйственных зданий и сооружений, предназначенных для работы при систематическом воздействии температур не свыше 50 °С и не ниже минус 70 °С. Проектирование армоцементных конструкций, находящихся под воздействием температур свыше 50 до 80 °С и в условиях агрессивной среды, кроме настоящих рекомендаций должно учитывать дополнительные требования, предъявляемые к конструкциям из бетона (СНиП 2.03.04-84).
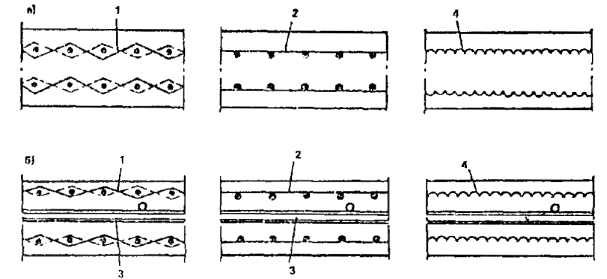
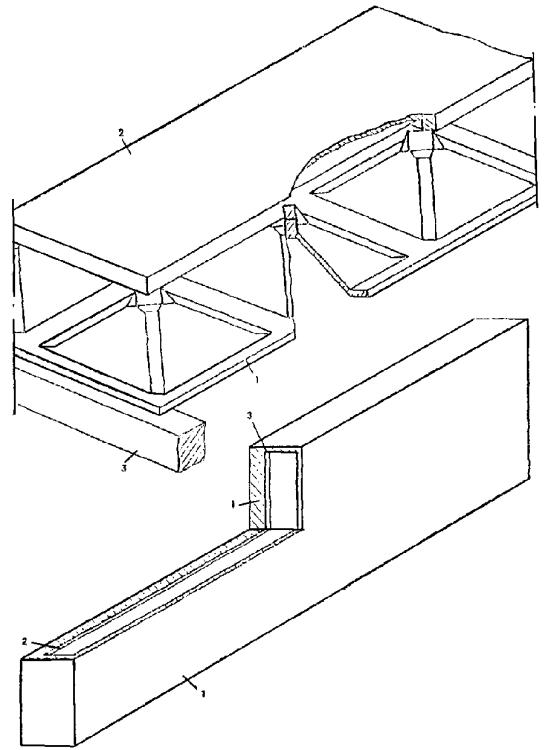
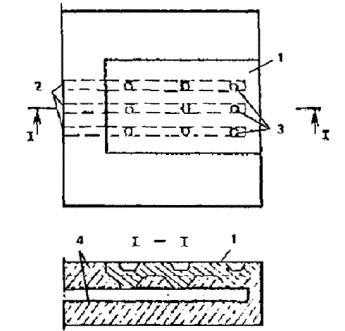
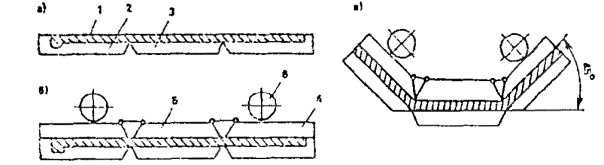
1.2. Армоцементными конструкциями принято называть тонкостенные железобетонные конструкции (толщина до 30 мм), изготовляемые из мелкозернистого бетона, в качестве арматуры которых применяются: частые тонкие, сварные или плетеные проволочные сетки, равномерно распределенные по сечению элемента (сетчатое армирование); частые тонкие тканые, сварные или плетеные проволочные сетки, равномерно распределенные по сечению, в сочетании со стержневой или проволочной арматурой (комбинированное армирование) (рис. 1).
1.3. Армоцементные конструкции, как правило, должны применяться в неагрессивной среде.
Армоцементные конструкции допускается применять в слабоагрессивной газообразной среде при толщине защитного слоя бетона для арматуры согласно требованиям СНиП 2.03.03-85 при защите сетки и проволоки цинковым покрытием толщиной не менее 30 мкм или защите поверхности лакокрасочным покрытием согласно требованиям, установленным СНиП 2.03.11-85, а в слабоагрессивной твердой среде при одновременной защите соответственно арматуры и поверхности конструкции.
Рис. 1. Армирование армоцементных конструкций
а - сетчатое; б - комбинированное; 1 - частые тонкие тканые сетки; 2 - частые тонкие сварные сетки; 3 - стержневая или проволочная арматура; 4 - сетки плетеные
1.4. Наружные кровельные и ограждающие армоцементные элементы, эксплуатируемые в условиях отсутствия агрессивной среды, выполненные с учетом п. 2.1 СНиП 2.03.03-85 к качеству мелкозернистого бетона, толщине и армированию защитного слоя бетона для арматуры, допускается применять без оцинковки арматуры и устройства защитных покрытий.
1.5. Выбор конструктивных решений армоцементных конструкций должен производиться исходя из технико-экономической целесообразности применения таких конструкций в конкретных условиях строительства с учетом максимального снижения их материалоемкости, трудоемкости, энергоемкости и стоимости.
Армоцементные конструкции рекомендуется применять в элементах зданий и сооружений, для которых преимущественное значение имеют: снижение энергоемкости, снижение собственного веса, уменьшение расхода стали и бетона благодаря применению эффективного утеплителя, уменьшение раскрытия трещин и обеспечение водонепроницаемости бетона.
1.6. При выборе конструктивных решений должны учитываться методы изготовления, монтажа и условия эксплуатации конструкций.
Форма и размеры элементов должны предусматриваться исходя из наиболее полного использования свойств армоцементных конструкций, возможности заводского механизированного изготовления, удобства транспортирования и монтажа конструкции или монолитного возведения.
1.7. Армоцементные конструкции рекомендуется выполнять из унифицированных элементов, в том числе из плоских листов, придавая им в необходимых случаях пространственную форму путем сгиба. Из армоцементных листов целесообразно создавать однослойные и трехслойные элементы ограждающих конструкций, несъемную опалубку монолитных пространственных конструкций покрытий и перекрытий.
1.8. Экономически целесообразно применять армоцементные конструкции в чердачных покрытиях неотапливаемых и отапливаемых зданий и навесах без рулонной гидроизоляции, в конструкциях для которых существенное значение имеют снижение веса, уменьшение трудоемкости устройства и стоимости. Проектирование облегченных армоцементных конструкций в комплексных безрулонных покрытиях должно предусматривать применение легкого эффективного утеплителя.
1.9. Армоцементные конструкции допускается применять в качестве несъемной опалубки для массивных монолитных железобетонных конструкций с обеспечением в случае необходимости специальных мероприятий для надежной совместной ее работы с бетоном основной конструкции.
1.10. Армоцементная несъемная опалубка может иметь достаточно прочное соединение на сдвиг по линии контакта опалубки с монолитным бетоном при соответствующей подготовке омоноличиваемой поверхности в классе бетона несъемной опалубки выше на порядок, чем монолитного, и выполнении требований п. 1.6 СНиП 2.03.03-85. Расчетную прочность на сдвиг по контуру «старого» и «нового» допускается применять по экспериментальным данным, но не более Rbq = 2Rbt, где Rbt - прочность монолитного бетона.
1.11 (1.8)*. При проектировании сборных армоцементных конструкций особое внимание необходимо обращать на прочность и долговечность и технологичность соединений и узлов. Соединения и узлы сборных ограждающих конструкций должны удовлетворять также специальным требованиям к этим ограждениям (обеспечивать передачу усилий элементами несущих конструкций, выполнение теплотехнических требований, заданной деформативности и др.).
* Здесь и далее в скобках даны номера пунктов СНиП 2.03.03-85.
1.12 (1.9). Как правило, должен применяться беспетлевой подъем армоцементных конструкций.
1.13. Армоцементные листовые конструкции целесообразно проектировать с учетом применении кантователя и специальной траверсы для подъема, оборудованной стропами со скобами, захватывающими армоцементный лист за край с шагом не более 3 м. Возможно также применение для подъема армоцементных листов вакуумприсосов.
ПРИМЕРЫ АРМОЦЕМЕНТНЫХ КОНСТРУКЦИЙ
1.14. Тонкостенные армоцементные конструкции могут применяться в покрытиях, перекрытиях, подвесных потолках, стенах, перегородках и других частях зданий и сооружений, в инженерных конструкциях в виде лотков небольшой емкости для жидких и сыпучих материалов, элементов санитарно-технического оборудования, декоративных элементов и т.п. Армоцементные конструкции проектируются, как правило, из элементов заводского изготовления.
1.15. В ряде случаев исходя из местных условий армоцементные конструкции целесообразно проектировать как монолитные, выполняемые без опалубки с нанесением мелкозернистого бетона на частые сетки пневмонабрызгом или вручную.
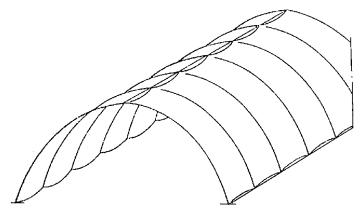
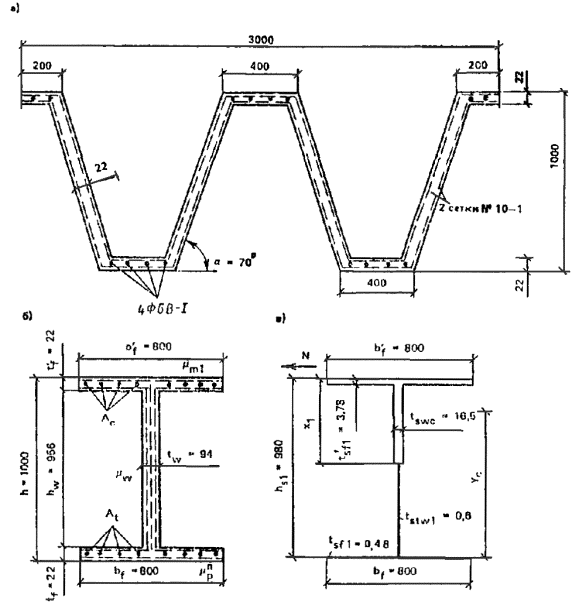
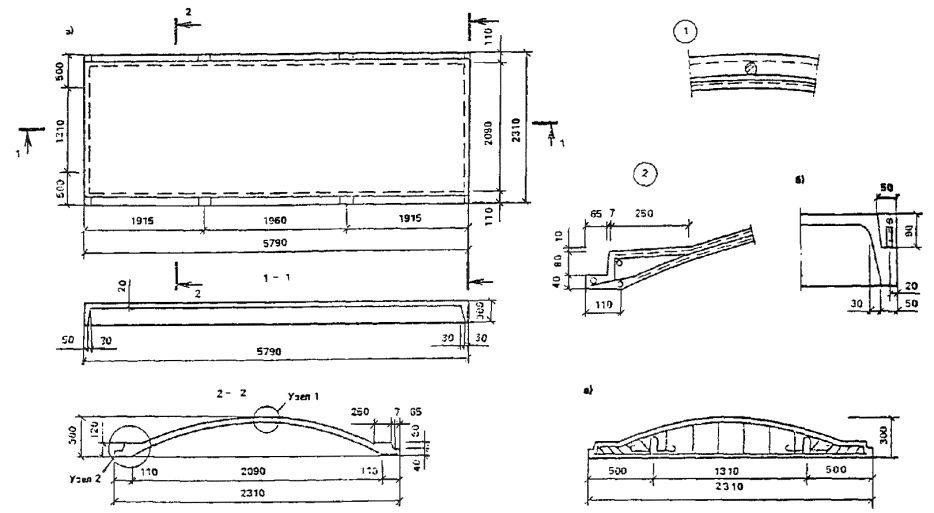
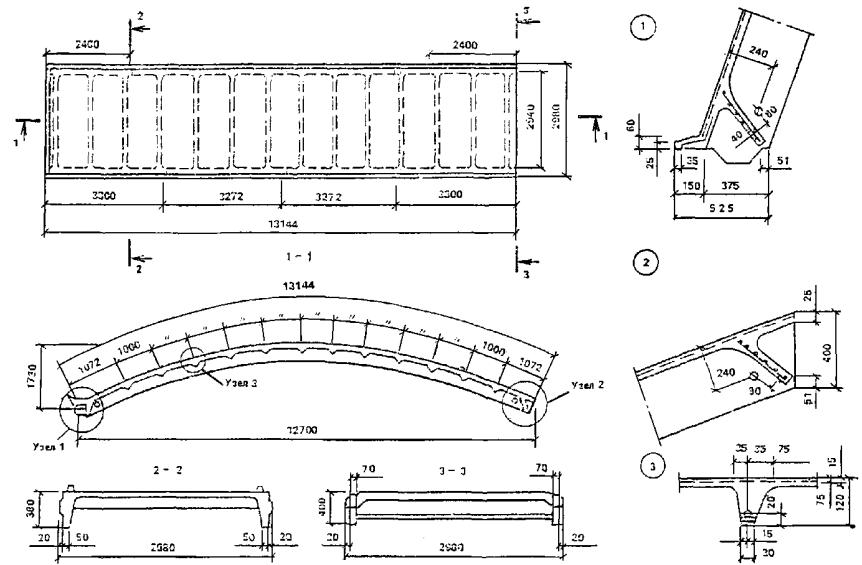
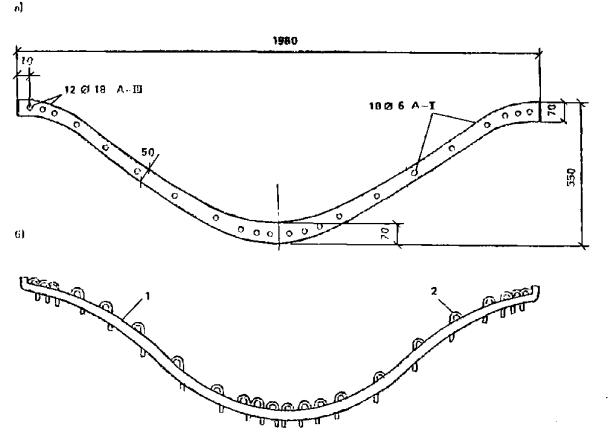
1.16. Для сводчатых конструкций массового строительства целесообразно предусматривать элементы двоякой кривизны (рис. 2) или цилиндрические ребристые элементы (рис. 3) шириной 2 - 3 м, длиной до 24 м и толщиной 2 - 3 см. Из элементов двоякой кривизны могут собираться волнистые своды пролетом до 48 м.
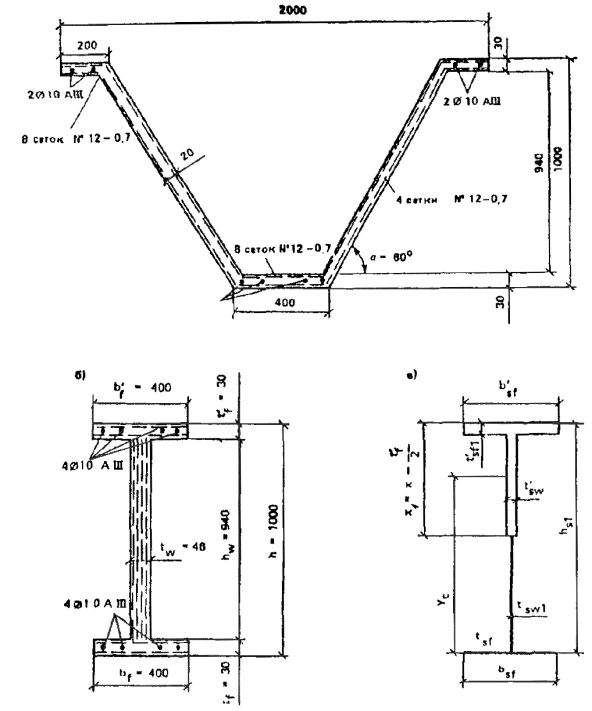
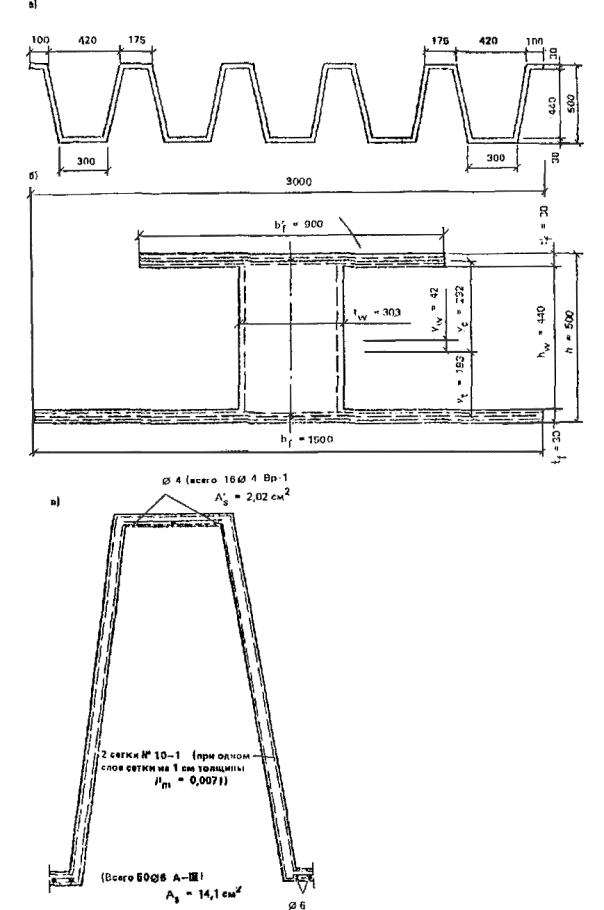
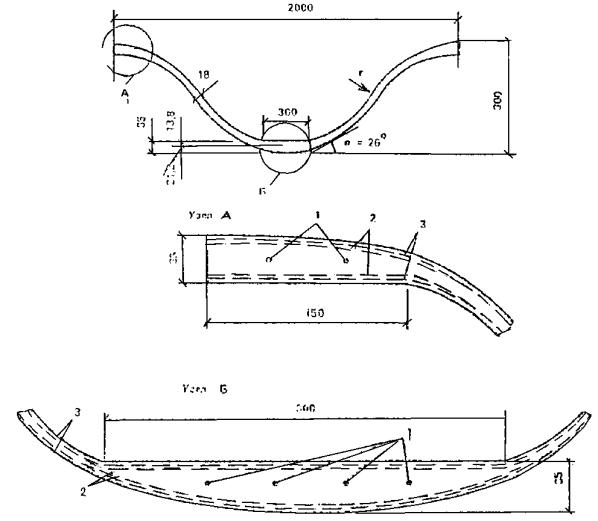
1.17. Складчатые элементы шириной 1 - 1,5 м, длиной до 8 м, толщиной до 25 мм применяются для покрытия с соединениями швом внахлестку (рис. 4). Складки изготавливаются методом сгиба свежеотформованного листа, имеют комбинированное армирование сетками и продольными проволоками из стержней класса Вр-I диаметром 5 - 6 мм с монтажным (при длине складок до 3 м) или расчетным предварительным напряжением. Складки могут применяться для крыш жилых зданий с чердаком, для павильонов и навесов без рулонной гидроизоляции и в качестве элементов стен неотапливаемых зданий и павильонов.
Рис. 2. Сборные сводчатые покрытия пролетом 12 - 18 м с безрулонной кровлей из армоцементных элементов двоякой кривизны
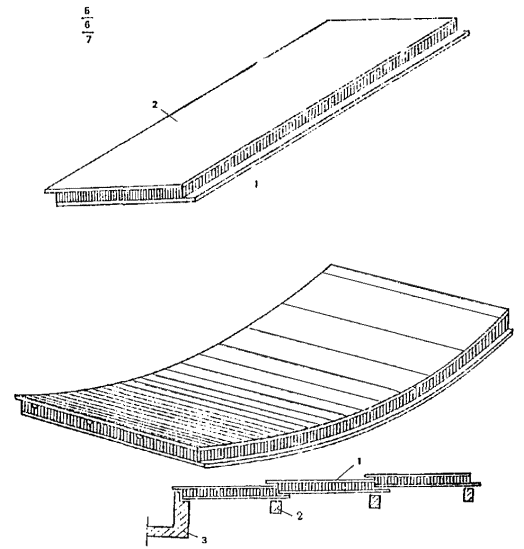
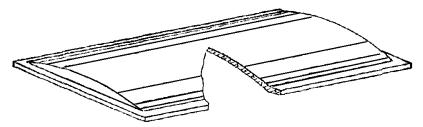
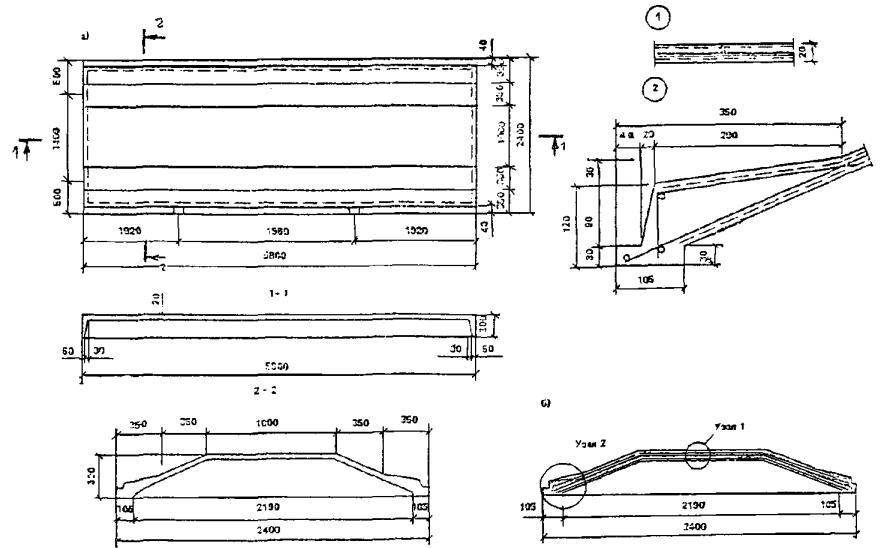
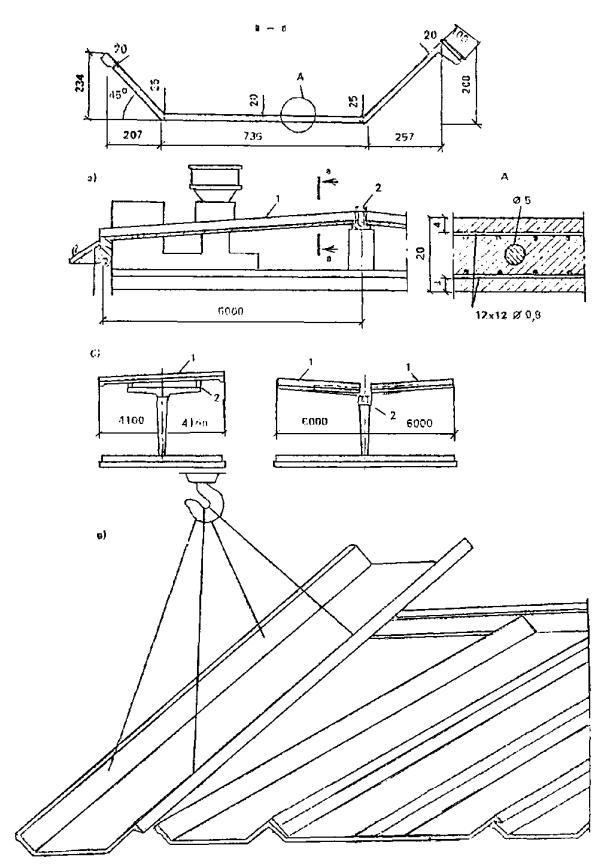
1.18. Трехслойные комплексные плоские (рис. 5) и цилиндрические (рис. 6) плиты из армоцементных листов и эффективного плитного утеплителя, укладываемые внахлестку (рис. 7), применяются в качестве скатного покрытия жилых зданий с теплым чердаком или бесчердачных безрулонных покрытий производственных зданий. Плиты имеют размер до 3 ´ 12 м. Армоцементные листы толщиной до 25 - 30 мм имеют комбинированное армирование, как правило, с предварительно напряженной арматурой класса Вр-II диаметром 5 - 6 мм. Стыки плит должны иметь уплотнение, удовлетворяющее требованиям паро- и теплоизоляции. В толще утеплителя рекомендуется устраивать вентилирующие продухи.
1.19. Армоцементный сборный или монолитный слой может быть применен в качестве индустриальной, устраиваемой на заводе стяжки по утеплителю для плит на пролет типа КЖС (рис. 8) или П. Сборный армоцементный лист может укладываться со сгибом на полужесткий или мягкий утеплитель. Предварительно напряженный армоцементный лист целесообразно применять для безрулонных покрытий.
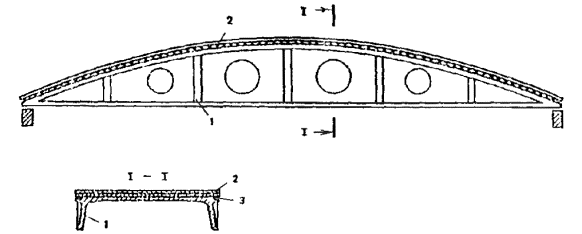
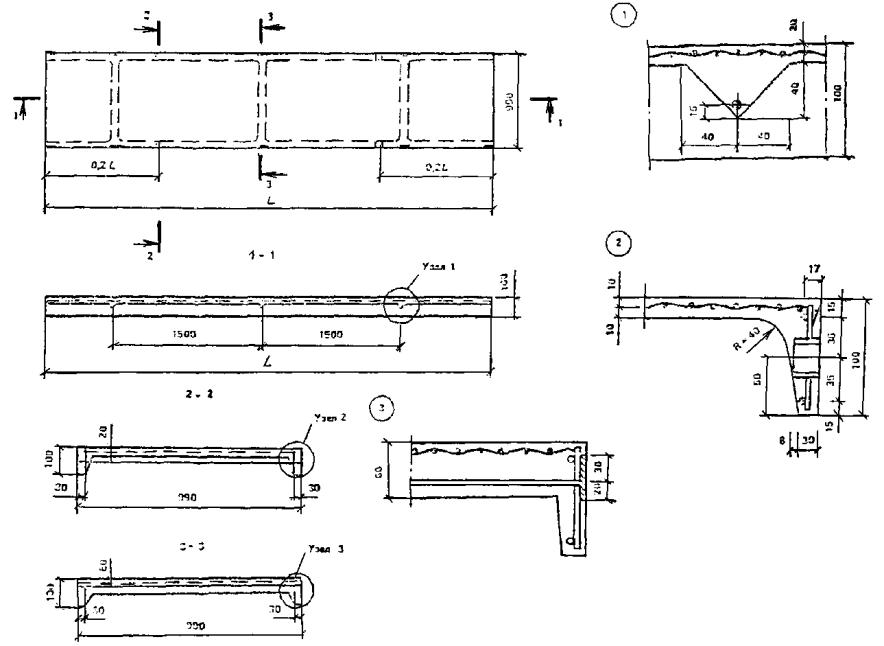
1.20. Складчатые армоцементные призматические элементы могут применяться для большепролетных (до 36 м) покрытий с передачей распора на затяжки (рис. 9) или на опоры-контрфорсы (рис. 10). Из призматических армоцементных балочных складок могут проектироваться покрытия пролетом до 24 м (см. рис. 7).
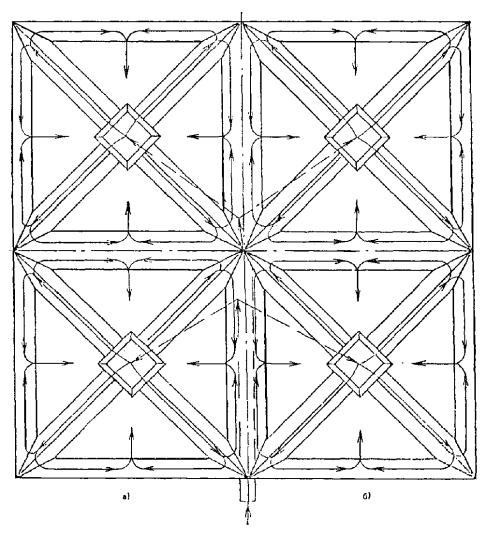
1.21. Армоцементные пирамидальные элементы структуры (рис. 11) применяются для перекрытий и покрытий над зальными помещениями пролетом до 24 м. Армоцементные пирамиды размером до 1,5 ´ 1,5 м объединяются на заводе в блоки, например размером 3 ´ 9 м, из которых собираются с помощью сварки элементы балочного покрытия на пролет. В этих элементах может быть применена предварительно напряженная арматура. Армоцементные структурные плиты покрытия опираются на подстропильные балки, на колонны или на стены.
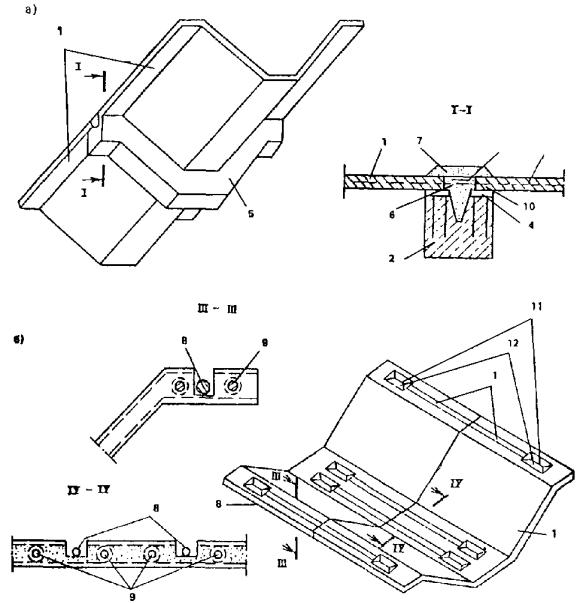
Армоцементные слоистые панели для стен показаны на рис. 12. Из армоцементных листов могут быть выполнены как наружные, так и внутренние слои, а также соединительные стенки. Соединения между слоями обеспечиваются заделкой края сеток в бетон при послойном изготовлении панелей или с помощью сварки закладных деталей или монолитного керамзитобетонного ребра по контуру панели при сборке панелей из готовых листов.
1.22. Армоцементные плиты-оболочки (рис. 13) находят применение в подвесных потолках покрытий с проходным межферменным этажом. Плиты-оболочки имеют размер 1,5 ´ 6 м, толщину 20 мм, комбинированное армирование и устраиваются с проемами для светового оборудования.
1.23. Панели армоцементных перегородок, которые могут быть однослойными волнистыми и коробчатыми (рис. 14), и многослойными слоистыми (рис. 15), применяются в зависимости от условий эксплуатации. Слоистые армоцементные перегородки, в том числе с утеплителем между армоцементными листами, обладают более высокими показателями звукоизоляции и огнестойкости.
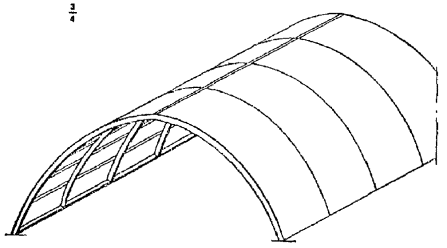
Рис. 3. Сводчатое покрытие зданий пролетом 12 - 18 м с безрулонной кровлей из армоцементных цилиндрических элементов
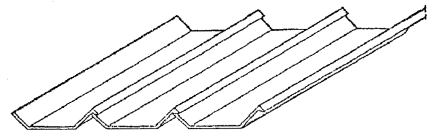
Рис. 4. Армоцементные предварительно напряженные складки
Рис. 5. Трехслойные плоские плиты безрулонного покрытия
1 - нижний лист; 2 - верхний лист
Рис. 6. Трехслойные цилиндрические плиты безрулонного покрытия
Рис. 7. Общий вид и разрез вдоль ската безрулонного покрытия из трехслойных плит
1 - трехслойная плита; 2 - железобетонное ребро; 3 - водоприемный лоток
Рис. 8. Применение армоцементного листа в качестве выравнивающего слоя по утеплению и плитам, оболочкам на пролет
1 - несущая железобетонная плита-оболочка КЖС; 2 - армоцементный лист; 3 - утеплитель
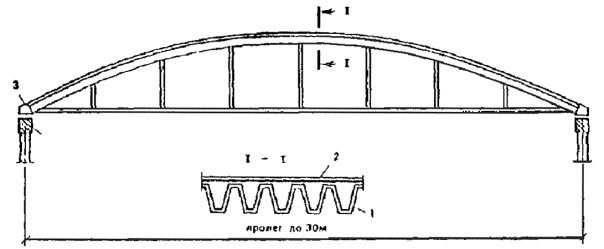
Рис. 9. Схема армоцементного свода покрытия с затяжкой
1 - армоцементные волнистые элементы свода; 2 - плита-утеплитель и гидроизоляция; 3 - опорная балка; 4 - подстропильная балка
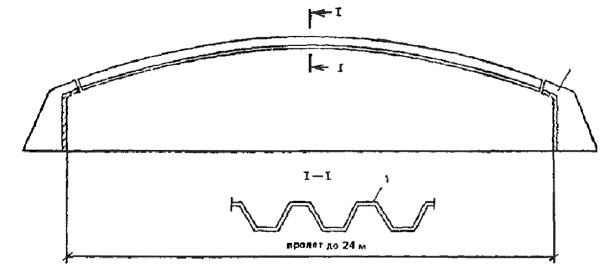
Рис. 10. Схема армоцементного волнистого свода
1 - волнистые элементы свода
Рис. 11. Структурная плита покрытия
1 - армоцементные пирамидальные элементы; 2 - железобетонная верхняя плита; 3 - железобетонная подстропильная балка
Рис. 12. Слоистая стеновая панель
1 - армоцементный наружный лист; 2 - утеплитель; 3 - разделительный элемент; 4 - керамзитобетонный слой
Рис. 13. Сводчатая плита подвесного потолка
Рис. 14. Армоцементные панели перегородки
а - волнистая; б - коробчатая
Рис. 15. Схема слоистой армоцементной звукоизолирующей панели перегородки
1 - армоцементный лист; 2 - минераловатные плиты
ОСНОВНЫЕ РАСЧЕТНЫЕ ТРЕБОВАНИЯ
1.24 (1.10). Армоцементные конструкции должны удовлетворять требованиям расчета по несущей способности (предельные состояния первой группы) и по пригодности к нормальной эксплуатации (предельные состояния второй группы) согласно положениям СНиП 2.03.01-84 и настоящих норм, учитывающих особенности армоцементных конструкций: а) дисперсность армирования; б) тонкостенность конструкций; в) уменьшенный защитный слой бетона.
1.25 (1.11). Расчет армоцементных конструкций должен производиться на все возможные неблагоприятные сочетания нагрузок от собственного веса и внешней нагрузки с учетом продолжительности их воздействия для всех стадий работы конструкции: изготовления, транспортирования, возведения и эксплуатации.
1.26. Значения нагрузок и воздействий коэффициентов перегрузок, коэффициентов сочетаний, а также разделение нагрузок на постоянные и временные (длительные, кратковременные, особые) должны приниматься в соответствии с требованиями СНиП 2.01.07-85 и с учетом дополнительных указаний СНиП 2.03.01-84.
Нагрузки, учитываемые при расчете армоцементных конструкций по образованию и раскрытию трещин, следует принимать согласно указаниям п. 1.28, а учитываемые при расчете по деформациям - согласно СНиП 2.03.01-84.
1.27. Сборные армоцементные конструкции рассчитываются на воздействия усилий при их подъеме и транспортировании. При этом коэффициент динамичности принимается равным: при транспортировании - 1,5; при подъеме и монтаже - 1,3.
1.28 (1.13). В зависимости от условий, в которых работает конструкция, и от вида применяемой арматуры к трещиностойкости армоцементных конструкций предъявляют требования соответствующих категорий: 1-я категория - не допускается образование трещин; 2-я категория - допускается ограниченное по ширине непродолжительное и продолжительное раскрытие трещин.
Категории требований к трещиностойкости армоцементных конструкций в зависимости от условий их работы и вида арматуры, а также значения предельно допустимой ширины раскрытия трещин приведены в табл. 1.
Нагрузки, учитываемые при расчете армоцементных конструкций по образованию и раскрытию трещин, должны приниматься согласно табл. 2.
Категории требований к трещиностойкости армоцементных конструкций относятся к нормальным и наклонным к продольной оси элемента трещинам.
Во избежание раскрытия продольных трещин должны приниматься конструктивные меры (установка соответствующей сетчатой арматуры), а для предварительно напряженных элементов, кроме того, значения сжимающих напряжений в бетоне в стадии предварительного обжатия должны быть ограничены, см. п. 1.53 (1.23).
Таблица 1
|
Категория требований к трещиностойкости армоцементных конструкций и предельно допустимая ширина acrc1 и acrc2 раскрытия трещин при армировании, мм |
|||||
|
комбинированном |
сетчатом |
комбинированном |
|||
|
сетками и стержневой арматурой классов А-I, А-II, А-III и с проволочной арматурой класса Вр-I |
оцинкованными сетками и оцинкованной проволочной арматурой классов В-II, Вр-II, К-7 |
сетками со стержневой арматурой классов А-IV, А-V с проволочной арматурой классов В-II и Вр-II, К-7 при диаметре проволоки 4 мм и более |
сетками и стержневой арматурой класса Аr-VI, проволочной арматурой классов В-II и Вр-II и К-7 при диаметре проволоки менее 4 мм |
||
|
С полностью растянутым или частично сжатым сечением, воспринимающим давление жидкостей или газов |
2-я категория |
2-я категория * |
1-я категория** |
1-я категория |
1-я категория |
|
acrc1 = 0,05 |
acrc1 = 0,05 |
- |
- |
- |
|
|
acrc2 = 0,03 |
acrc2 = 0,03 |
- |
- |
- |
|
|
Эксплуатируемые в отапливаемых зданиях с относительной влажностью воздуха помещений выше 75 %, а также на открытом воздухе и в неотапливаемых зданиях в условиях увлажнения атмосферными осадками |
2-я категория |
2-я категория |
1-я категория** |
1-я категория |
1-я категория |
|
acrc1 = 0,1 |
acrc1 = 0,12 |
- |
- |
- |
|
|
acrc2 = 0,05 |
acrc2 = 0,06 |
- |
- |
- |
|
|
Эксплуатируемые в отапливаемых зданиях с относительной влажностью внутреннего воздуха помещений св. 60 до 75 % |
2-я категория |
2-я категория |
2-я категория |
2-я категория |
1-я категория |
|
acrc1 = 0,15 |
acrc1 = 0,15 |
acrc1 = 0,07 |
acrc1 = 0,07 |
- |
|
|
acrc2 = 0,1 |
acrc2 = 0,1 |
acrc2 = 0,05 |
acrc2 = 0,05 |
- |
|
|
Эксплуатируемые в отапливаемых зданиях с относительной влажностью внутреннего воздуха помещений до 60 % и при отсутствии возможности систематического увлажнения конструкции конденсатом |
2-я категория |
2-я категория |
2-я категория |
2-я категория |
2-я категория |
|
acrc1 = 0,2 |
acrc1 = 0,22 |
acrc1 = 0,15 |
acrc1 = 0,15 |
acrc1 = 0,05 |
|
|
acrc2 = 0,15 |
acrc2 = 0,15 |
acrc2 = 0,1 |
acrc2 = 0,1 |
acrc2 = 0,03 |
|
|
* Категория требований к трещиностойкости принята при защитном покрытии сеток оцинковкой в 30 мкм. ** Применение сетчатого армирования допускается при специальном обосновании. |
|||||
Таблица 2
|
Категория требований к трещиностойкости армоцементных конструкций |
Нагрузки и коэффициент надежности по нагрузке γf, принимаемой при расчете |
||
|
по образованию трещин |
по раскрытию трещин |
||
|
непродолжительному |
продолжительному |
||
|
1-я |
Постоянные, длительные и кратковременные нагрузки при γf > 1* |
- |
- |
|
2-я |
Постоянные, длительные и кратковременные нагрузки при γf = 1 (расчет производится для выяснения необходимости проверки по раскрытию трещин) |
Постоянные, длительные и кратковременные нагрузки при γf = 1 |
Постоянные и длительные нагрузки при γf = 1 |
|
* Коэффициент надежности по нагрузке γf принимается как при расчете на прочность. Примечания: 1 Длительные и кратковременные нагрузки принимаются с учетом указаний, изложенных в п. 1.12 СНиП 2.03.01-84. 2. Особые нагрузки учитываются при расчете по образованию трещин, приводящих к катастрофам (взрыв, пожар и т.п.). |
|||
Примечание. Под непродолжительным раскрытием трещин понимается их раскрытие при кратковременном действии постоянных, длительных и кратковременных нагрузок, а под продолжительным раскрытием - только постоянных и длительных нагрузок.
1.29 (1.14). Усилия в статически неопределимых армоцементных конструкциях от нагрузок и вынужденных перемещений (вследствие изменения температуры, влажности бетона, смещения опор и т.п.) при расчете по предельным состояниям первой и второй групп следует, как правило, определять с учетом неупругих деформаций бетона и арматуры и наличия трещин, а также с учетом в необходимых случаях деформированного состояния как отдельных элементов, так и конструкций.
Для конструкций, методика расчета которых с учетом неупругих свойств армоцемента не разработана, а также на промежуточных стадиях расчета (итерационные методы, метод поправочных коэффициентов и т.п.) усилия в статически неопределимых конструкциях допускается определять в предположении их линейной упругости.
1.30. Расчет конструкций, усилия в сечениях которых были определены с использованием упругих методов расчет, должен выполняться с учетом возможного перераспределения усилий в статически неопределимой конструкции после раскрытия трещин.
Такими зонами перераспределения в оболочках покрытий являются приконтурные зоны.
1.31. Статический расчет армоцементных конструкций в виде оболочек и складок должен производиться как тонкостенных пространственных конструкций.
1.32 (1.16). При расчете по прочности армоцементных конструкций на воздействие сжимающей продольной силы N необходимо учитывать случайный эксцентриситет ea согласно требованиям СНиП 2.03.01-84.
1.33. Определение прогибов армоцементных конструкций следует производить согласно требованиям пп. 4.8 - 4.16 СНиП 2.03.03-85 и СНиП 2.03.01-84.
Значения предельных допустимых прогибов следует принимать в соответствии с п. 1.20 СНиП 2.03.01-84.
1.34. Среднюю плотность мелкозернистого бетона, учитываемую при расчете армоцементных конструкций, следует принимать равной 2300 кг/м3. Средняя плотность армоцемента при двух сетках принимается равной 2400 кг/м3; при наличии большого количества сеток среднюю плотность армоцемента следует увеличивать на 50 кг/м3 на каждую дополнительную сетку.
1.35. Расстояния между температурно-усадочными швами армоцементных конструкций покрытий должны устанавливаться, как правило, расчетом их напряженно деформированного состояния от этих воздействий.
ДОПОЛНИТЕЛЬНЫЕ УКАЗАНИЯ ПО ПРОЕКТИРОВАНИЮ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫХ КОНСТРУКЦИЙ
1.36. Предварительно напряженные армоцементные конструкции следует проектировать в соответствии с требованиями СНиП 2.03.01-84 и с учетом дополнительных указаний пп. 1.36 - 1.41. Сетки в сечении преднапряженных армоцементных конструкций должны учитываться в схеме усилий так же, как ненапрягаемая арматура.
1.37 (1.21). В случае если сжатая при эксплуатационных нагрузках зона предварительно напряженных элементов не обеспечена расчетом от образования трещин, нормальных к продольной оси, в стадиях изготовления, транспортирования и возведения следует учитывать снижение трещиностойкости растянутой при эксплуатации зоны элементов, а также увеличение их кривизны.
Таблица 3
|
Факторы, вызывающие потери предварительного напряжения арматуры |
Значения потерь предварительного напряжения, МПа, при натяжении арматуры |
||
|
на упоры |
на бетон |
||
|
Усадка мелкозернистого бетона группы: |
Бетон естественного твердения |
Бетон, подвергнутый тепловой обработке при атмосферном давлении |
Независимо от условий твердения бетона |
|
А классов В35 и ниже |
52 |
45 |
40 |
|
А класса В40 |
65 |
52 |
40 |
|
Б классов В45 и ниже |
75 |
60 |
50 |
|
В » В35 » » |
40 |
35 |
50 |
|
класса В40 |
50 |
40 |
40 |
|
» В45 |
60 |
50 |
40 |
|
Ползучесть мелкозернистого бетона группы: |
|
|
|
|
А |
150α(σbp/Rbp)1,3 при σbp/Rbp ≥ 0,75; 300α(σbp/Rbp - 0,375)1,3 при σbp/Rbp > 0,75, где σbp - напряжение в бетоне, вычисленное с учетом потерь по поз. 1 - 6; α - коэффициент, принимаемый равным: для бетона естественного твердения - 1; для бетона, подвергнутого тепловой обработке при атмосферном давлении, - 0,85. |
||
|
Б |
150α(σbp/Rbp)1,5 при σbp/Rbp ≤ 0,75; 300α(σbp/Rbp - 0,375)1,5 при σbp/Rbp > 0,75; |
||
|
В |
150×0,85(σbp/Rbp) при σbp/Rbp ≤ 0,75; 300×0,85(σbp/Rbp - 0,375) при σbp/Rbp > 0,75. |
||
В элементах, рассчитываемых на воздействие многократно повторяющейся нагрузки, образование таких трещин не допускается.
1.38. Потери предварительного напряжения арматуры для армоцементных конструкций должны определяться согласно требованиям СНиП 2.03.01-84 как для мелкозернистого бетона.
Для упрощения вычислительных работ потери от усадки и ползучести приведены в табл. 3.
1.39 (1.23). Сжимающие напряжения в бетоне в стадии предварительного обжатия σbp не должны превышать величины (в долях от передаточной прочности бетона Rbp), указанных в СНиП 2.03.01-84.
Значения σbp определяются на уровне крайнего сжатого волокна бетона с учетом потерь предварительного напряжения арматуры по СНиП 2.03.01-84 и при коэффициенте точности натяжения арматуры γsp, равном единице.
1.40 (1.24). В предварительно обжатой зоне сечения армоцементных элементов площадь сечения сетчатой или комбинированной ненапрягаемой арматуры должна быть минимальной. Сетки должны располагаться симметрично относительно напрягаемой арматуры.
1.41 (1.25). На концевых участках предварительно напряженных элементов армоцементных конструкций с арматурой без анкеров, к которым предъявляются требования 2-й категории трещиностойкости, в пределах длины зоны передачи напряжений не допускается образование трещин при действии постоянной, длительной и кратковременной нагрузок, вводимых в расчет с коэффициентом надежности по нагрузке γf, принимаемым по табл. 2.
1.42. Напряжения в бетоне и арматуре, а также усилия предварительного обжатия бетона, вводимые в расчет предварительно напряженных конструкций, определяются с учетом следующих указаний.
Напряжения в сечениях, нормальных к продольной оси элемента, определяются по правилам расчета упругих материалов. При этом принимаются приведенное сечение, включающее сечение бетона с учетом ослабления его каналами, пазами и т.п., а также сечение всей продольной (напрягаемой и ненапрягаемой) арматуры, умноженное на отношение α модулей упругости арматуры и бетона. Если части бетонного сечения выполнены из бетонов разных классов или видов, их приводят к одному классу или виду исходя из отношения модулей упругости бетона.
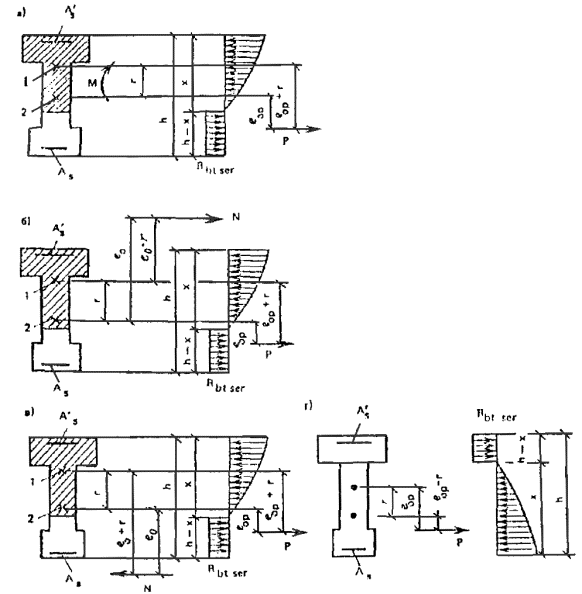
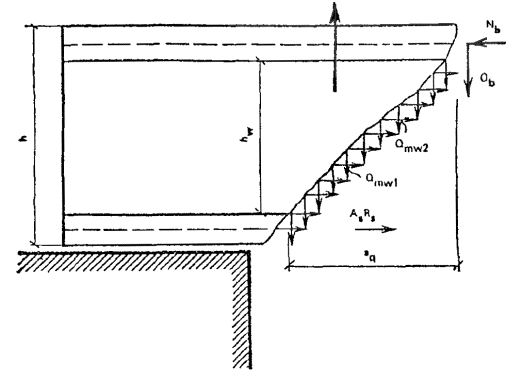
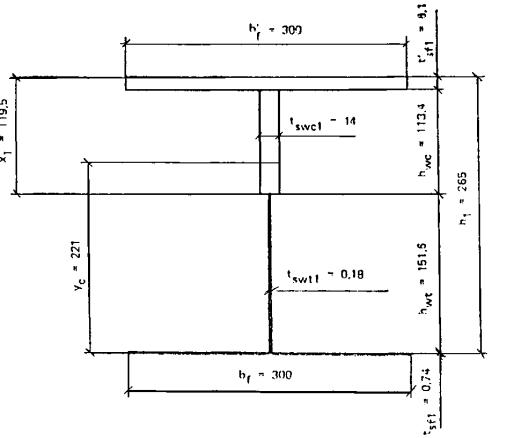
Усилие предварительного обжатия P и эксцентриситет его приложения eop относительно центра тяжести приведенного сечения (рис. 16) определяются по формулам:
P = σspAsp + σ'spA'sp - σsAs - σ'sA's - σmAm - σ'mA'm; (1)
eop = (σspAspysp + σ'sA'sy's - σ'spA'spy'sp - σsAsys - σmAmym - σ'mA'my'm)/P, (2)
где σs, σ's, σm, σ'm - напряжения в ненапрягаемой арматуре соответственно s, s' и сетках, вызванные усадкой и ползучестью бетона; ysp, y'sp, ys, y's, ym, y'm - расстояния от центра тяжести приведенного сечения до точек приложения равнодействующих усилий соответственно в напрягаемой и ненапрягаемой арматуре s, s' и сетках (рис. 16).
При криволинейной напрягаемой арматуре значения σsp и σ'sp умножают соответственно на cos0 и cos0', где 0 и 0' - углы наклона оси арматуры к продольной оси элемента (для рассматриваемого сечения).
Напряжения σsp и σ'sp принимают: в стадии обжатия бетона - с учетом первых потерь; в стадии эксплуатации элемента - с учетом первых и вторых потерь.
Напряжения σs и σ's принимают численно равными: в стадии обжатия бетона - потерям напряжений от быстронатекающей ползучести по поз. 6 табл. 5 СНиП 2.03.01-84; в стадии эксплуатации элемента - сумме потерь напряжений от усадки и ползучести бетона по табл. 3.
Рис. 16. Схема усилий предварительного напряжения в арматуре и сетках в поперечном сечении армоцементного элемента
а - изгибаемого сечения; б - внецентренно сжатого сечения; в - внецентренно растянутого сечения; г - от действия предварительного напряжения
2. МАТЕРИАЛЫ ДЛЯ АРМОЦЕМЕНТНЫХ КОНСТРУКЦИЙ
МЕЛКОЗЕРНИСТЫЙ БЕТОН
2.1 (2.1). Для армоцементных конструкций, - проектируемых в соответствии с требованиями настоящих норм, следует предусматривать конструкционный мелкозернистый бетон средней плотности от 2200 кг/м3 с крупностью зерен до 5 мм в соответствии с ГОСТ 25192-82.
Бетон должен иметь водопоглощение не более 8 %.
Примечания: 1. Мелкозернистые пески, не удовлетворяющие требованиям ГОСТ 8736-85, допускается применять с использованием пластифицирующих добавок в количестве 0,25 % веса цемента. Обогащение мелкозернистых песков допускается производить смешиванием их с 50 % крупного песка или высевками с размером зерен не более 1/2 размера ячейки сеток.
2. Для повышения морозостойкости армоцементных конструкций рекомендуется применять пластифицирующие добавки.
2.2 (2.2). Мелкозернистый бетон для армоцементных конструкций в зависимости от вида и условий их работы следует предусматривать следующих классов и марок:
а) классов на прочности на сжатие:
бетон группы А - естественного твердения или подвергнутый тепловой обработке при атмосферном давлении, на песке с модулем крупности свыше 2 - В20, В25, В30, В35 и В40;
бетон группы Б - естественного твердения или подвергнутый тепловой обработке при атмосферном давлении, на песке с модулем крупности 2 и менее - В20, В25 и В30;
бетон группы В - подвергнутый автоклавной обработке - В20, В25, В30, В35, В40, В45, В50, В55, В60.
Допускается применение бетона промежуточных классов В22,5 и В27,5 при условии, что это приводит к экономии цемента по сравнению с применением бетона соответственно классов В25 и В30 и не снижает другие технико-экономические показатели конструкции;
б) классов по прочности на осевое растяжение - Bt1,6; Bt2; Bt2,4; Bt2,8 и Bt3,2;
в) марок по морозостойкости - F100, F150, F200, F300, F400 и F500;
г) марок по водонепроницаемости - W6, W8, W10, W12.
Примечание. Определение понятий класс бетона и марки бетона см. ГОСТ 25192-82.
2.3 (2.3). Возраст бетона, отвечающий его классу по прочности на сжатие и осевое растяжение, назначается при проектировании исходя из возможных реальных сроков фактического загружения конструкции проектными нагрузками, способа возведения, условий твердения бетона. При отсутствии этих данных класс бетона устанавливается в возрасте 28 сут.
Значение отпускной прочности бетона в элементах сборных конструкций следует назначать в соответствии с указаниями ГОСТ 13015.0-83* и стандартов на конструкции конкретных видов.
2.4. Для предварительно напряженных армоцементных конструкций класс бетона по прочности на сжатие, в котором расположена напрягаемая арматура, должен приниматься в зависимости от вида и класса напрягаемой арматуры, ее диаметра и наличия анкерных устройств не ниже указанного в табл. 4.
Передаточная прочность бетона Rbp назначается в соответствии с требованиями СНиП 2.03.01-84.
Примечание. Передаточная прочность бетона Rbp (прочность бетона к моменту его обжатия) определяется на базовых образцах в соответствии с государственными стандартами с обеспеченностью 0,95.
Таблица 4
|
Класс бетона не ниже |
|
|
Проволочная арматура классов: |
|
|
В-II с анкерами |
В20 |
|
Вр-II без анкеров при диаметре проволоки: |
|
|
до 5 мм |
В20 |
|
6 мм и более |
В30 |
|
К-7 и К-19 |
В35 |
|
Стержневая арматура без анкеров диаметром 10 - 18 мм, классов: |
|
|
А-IV |
В20 |
|
А-V |
В25 |
|
А-VI |
В30 |
Таблица 5
|
Минимальные марки бетона |
|||||||
|
характеристика режима |
расчетная зимняя температура наружного воздуха |
по морозостойкости |
по водонепроницаемости |
||||
|
конструкций для зданий, и сооружений класса |
|||||||
|
I |
II |
III |
I |
II |
III |
||
|
Попеременное замораживание и оттаивание в водонасыщенном состоянии (например, конструкции без рулонных крыш и покрытий) |
Ниже минус 40 °С |
F300 |
F200 |
F150 |
W6 |
W4 |
W2 |
|
Ниже минус 20 °С до минус 40 °С |
F200 |
F150 |
F100 |
W4 |
W2 |
Не нормируется |
|
|
Ниже минус 5 °С до минус 20 °С |
F150 |
F100 |
F75 |
W2 |
Не нормируется |
||
|
Минус 5 °С и выше |
F100 |
F75 |
F50 |
W2 |
Не нормируется |
||
|
Попеременное замораживание и оттаивание в условиях эпизодического водонасыщения (например, ограждающие конструкции стены) |
Ниже минус 40 °С |
F200 |
F150 |
F100 |
W4 |
W2 |
Не нормируется |
|
Ниже минус 20 °С до минус 40 °С |
F100 |
F75 |
F50 |
W2 |
Не нормируется |
||
|
Ниже минус 5 °С до минус 20 °С |
F75 |
F50 |
Не нормируется |
||||
|
Минус 5 °С и выше |
F50 |
Не нормируется |
|||||
2.5 (2.5). Класс мелкозернистого бетона, применяемого для защиты от коррозии и обеспечения сцепления с бетоном напрягаемой арматуры, должен быть не менее В20.
2.6 (2.6). Для замоноличивания стыков армоцементных конструкций класс бетона следует устанавливать в зависимости от условий работы соединяемых элементов, но не менее чем класс бетона соединяемых элементов.
2.7. Для замоноличивания стыков элементов сборных конструкций, которые в процессе эксплуатации или монтажа могут подвергаться воздействию отрицательных температур наружного воздуха, следует принимать бетоны проектных марок по морозостойкости и водонепроницаемости не ниже марок, принятых для стыкуемых элементов.
2.8. Минимальные марки мелкозернистого бетона по морозостойкости и водонепроницаемости для армоцементных конструкций в зависимости от условий их работы должны приниматься в соответствии табл. 5.
НОРМАТИВНЫЕ И РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ МЕЛКОЗЕРНИСТОГО БЕТОНА
2.9. Нормативные и расчетные сопротивления мелкозернистого бетона, а также коэффициенты условий работы следует принимать в соответствии с указаниями СНиП 2.03.01-84.
Нормативные сопротивления мелкозернистого бетона Rbn и Rbtn в зависимости от класса бетона В даны в табл. 6.
2.10. Расчетные сопротивления мелкозернистого бетона для предельных состояний первой Rb и Rbt и второй Rb, ser, Rbt, ser групп определяются путем деления нормативных сопротивлений на соответствующие коэффициенты надежности по бетону при сжатии γbc или растяжении γbt, принимаемые при расчете по предельным состояниям первой группы γbc = 1,3, при назначении класса бетона по прочности на сжатие γbt = 1,5, на растяжение γbt = 1,3 и для второй группы предельных состояний γbc и γbt = 1.
2.11. Расчетные сопротивления мелкозернистого бетона Rb, Rbt, Rb, ser, Rbt, ser (с округлением) в зависимости от класса бетона по прочности на сжатие и осевое растяжение приведены: для предельных состояний первой группы - соответственно в табл. 7 и 8, для второй группы - в табл. 6.
Расчетные сопротивления мелкозернистого бетона для предельных состояний первой группы Rb и Rbt снижаются (или повышаются) путем умножения на коэффициенты условий работы бетона γbt, учитывающие особенности свойств бетона, длительность действия, многократную повторяемость нагрузки, условия к сжатию работы конструкции, способ ее изготовления, размеры сечения и т.п.
Таблица 6
|
Бетон |
Нормативные сопротивления мелкозернистого бетона Rbk и Rbtk и расчетные сопротивления для предельных состояний второй группы Rb, ser и Rbt, ser, МПа (кгс/см2), при классе бетона |
|||||||||
|
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
||
|
Сжатие осевое (призменная прочность) Rbn; Rb, ser |
Мелкозернистый |
15 (153) |
18,5 (189) |
22 (224) |
25,5 (260) |
29 (296) |
32 (326) |
36 (367) |
39,5 (403) |
43 (438) |
|
Растяжение осевое Rbtn; Rbt, ser |
Мелкозернистый, группы: |
|
|
|
|
|
|
|
|
|
|
А |
1,4 (14,3) |
1,6 (16,3) |
1,8 (18,4) |
1,95 (19,9) |
2,1 (21,4) |
- |
- |
- |
- |
|
|
Б |
1,15 (11,7) |
1,35 (13,8) |
1,5 (15,3) |
- |
- |
- |
- |
- |
- |
|
|
В |
1,4 (14,3) |
1,6 (16,3) |
1,8 (18,4) |
1,95 (19,9) |
2,1 (21,4) |
2,2 (22,4) |
2,3 (23,5) |
2,4 (24,5) |
2,5 (25,5) |
|
Таблица 7
|
Бетон |
Расчетные сопротивления мелкозернистого бетона для предельных состояний первой группы Rb и Rbt, МПа (кгс/см2), при классе бетона |
|||||||||
|
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
||
|
Сжатие осевое (призменная прочность) Rb |
Мелкозернистый |
11,5 (117) |
14,5 (148) |
17 (173) |
19,5 (199) |
22 (224) |
25 (255) |
27,5 (280) |
30 (306) |
33 (336) |
|
Растяжение осевое Rbt |
Мелкозернистый, группы: |
|
|
|
|
|
|
|
|
|
|
А |
90 (9,18) |
1,05 (10,7) |
1,2 (12,2) |
1,3 (13,3) |
1,4 (14,3) |
- |
- |
- |
- |
|
|
Б |
0,77 (7,85) |
0,9 (9,18) |
1 (10,2) |
- |
- |
- |
- |
- |
- |
|
|
В |
0,9 (9,18) |
1,05 (10,7) |
1,2 (12,2) |
1,3 (13,3) |
1,4 (14,3) |
1,45 (14,8) |
1,55 (15,8) |
1,6 (16,3) |
1,65 (16,8) |
|
|
Примечания: 1. В скобках даны значения нормативных сопротивлений, кгс/см2. 2. Группы мелкозернистых бетонов приведены в п. 2.2. |
||||||||||
Таблица 8
|
Расчетные сопротивления мелкозернистого бетона для предельных состояний первой группы Rbt при классе бетона по прочности на осевое растяжение |
|||||
|
Bt = 1,6 |
Bt = 2 |
Bt = 2,4 |
Bt = 2,8 |
Bt = 3,2 |
|
|
Растяжение осевое |
1,35 12,7 |
1,55 15,8 |
1,85 18,9 |
2,15 21,9 |
2,45 25 |
|
Примечание. Над чертой указаны значения в МПа, под чертой - в кгс/см2. |
|||||
Значения коэффициентов условий работы γbi приведены в табл. 9.
Расчетные сопротивления мелкозернистого бетона для предельных состояний второй группы Rb, ser и Rbt, ser вводятся в расчет с коэффициентом условий работы бетона γbi = 1.
Примечание. При использовании в расчетах промежуточных классов бетона по прочности на сжатие согласно п. 2.2 значения характеристик, приведенных и табл. 6 - 8, принимаются по линейной интерполяции.
2.12. Значения начального модуля упругости мелкозернистого бетона Eb при сжатии и растяжении принимаются по табл. 10. Для не защищенных от солнечной радиации конструкций, предназначенных для работы в климатическом подрайоне IVA согласно СНиП 2.01.01-82, значения Eb, указанные в табл. 10, следует умножать на коэффициент 0,85.
2.13 (2.12). Коэффициент линейной температурной деформации αbt мелкозернистого бетона в интервале температур от минус 40 °С до плюс 50 °С принимается равным 1×10-5 град-1.
При наличии данных о минералогическом составе заполнителей, расходе цемента, степени водонасыщения, морозостойкости бетона и т.д. допускается принимать другие значения αbt, обоснованные в установленном порядке. Для расчетной температуры ниже минус 10 °С и выше 50 °С значение αbt принимается по экспериментальным данным.
2.14. Начальный коэффициент поперечной деформации бетона (коэффициент Пуассона) принимается равным 0,2, а модуль сдвига мелкозернистого бетона G - равным 0,4 соответствующего значения Eb.
Таблица 9
|
Факторы, обуславливающие введение коэффициента условий работы бетона |
Коэффициенты условий работы бетона |
|
|
условное обозначение |
числовое значение |
|
|
Длительность действия нагрузки а) при учете постоянных, длительных и кратковременных нагрузок, кроме нагрузок непродолжительного действия, суммарная длительность действия которых за период эксплуатации мала (например, крановые нагрузки, нагрузки от крановых средств, ветровые нагрузки); нагрузки, возникающие при изготовлении, транспортировании и возведении, а также при учете особых нагрузок, вызванных деформациями просадочных, набухающих, вечномерзлых и подобных грунтов: |
γb1 |
- |
|
для мелкозернистого бетона естественного твердения и подвергнутого тепловой обработке: в условиях эксплуатации конструкции, благоприятных для нарастания прочности бетона (например, под водой, во влажном грунте или при влажности воздуха окружающей среды свыше 67 до 75 %) |
1 |
|
|
в остальных случаях |
0,9 |
|
|
б) при учете в рассматриваемом сочетании кратковременных нагрузок (непродолжительного действия) или особых нагрузок *, не указанных в поз. 2а для всех видов бетона |
1,1 |
|
|
Бетонирование в вертикальном положении (высота слоя бетонирования свыше 1,5 м) для мелкозернистого бетона |
γb2 |
0,85 |
|
Попеременное замораживание и оттаивание при температуре, °С: |
γb3 |
|
|
а) в водонасыщенном состоянии |
|
|
|
ниже минус 40 |
0,7 |
|
|
ниже минус 20 до минус 40 |
0,85 |
|
|
ниже минус 5 до минус 20 |
0,9 |
|
|
минус 5 и выше |
0,95 |
|
|
б) в условиях эпизодического водонасыщения |
|
|
|
ниже минус 40 |
0,9 |
|
|
минус 40 и выше |
1 |
|
|
Влияние двухосного сложного напряженного состояния сжатие-растяжение на прочность бетона при отношении напряжений: |
γb4 |
|
|
+ 0 |
1 |
|
|
-0,5 |
0,9 |
|
|
-1 |
0,8 |
|
|
Эксплуатация не защищенных от солнечной радиации конструкций климатического подрайона IVA согласно СНиП 2.01.01-82 |
γb5 |
0,85 |
|
Стадия предварительного обжатия конструкций: |
γb6 |
|
|
а) с проволочной арматурой |
1,1 |
|
|
б) со стержневой арматурой |
1,2 |
|
|
Бетон для замоноличивания стыков элементов при толщине шва менее 1/5 наименьшего размера сечения элемента и менее 10 см |
γb7 |
1,15 |
|
* При введении дополнительного коэффициента условий работы, связанного с учетом особых нагрузок согласно указаниям соответствующих нормативных документов (например, при учете сейсмических нагрузок), принимается γb1 = 1. Примечания: 1. Коэффициенты условий работы бетона по поз. 1, 3, 5 должны учитываться при определении расчетных сопротивлений Rb и Rbt, по поз. 4 - при определении Rbt, ser, а по остальным позициям - только при определении Rb. 2. Для конструкций, находящихся под действием многократно повторяющейся нагрузки, коэффициент γb1 учитывается при расчете прочности. 3. При расчете конструкций в стадии предварительного обжатия коэффициент γb1 не учитывается. 4. Коэффициенты условий работы бетона вводятся независимо друг от друга, но при этом их произведение должно быть не менее 0,45. 5. Для мелкозернистого бетона в армоцементных конструкциях коэффициент условий работы бетона γb8 принимается по специальным экспериментальным данным, но не более чем значение коэффициента γb1 для тяжелого бетона по табл. 16 СНиП 2.03.01-84. |
||
Таблица 10
|
Начальные модули упругости бетона при сжатии и растяжении Eb×10-3 при классе бетона |
|||||||||
|
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
|
Мелкозернистый, группы: |
|
|
|
|
|
|
|
|
|
|
А - естественного твердения |
22 224 |
24 245 |
26,0 265 |
27,5 280 |
28,5 290 |
- |
- |
- |
- |
|
подвергнутый тепловой обработке при атмосферном давлении |
20 201 |
21,5 219 |
23 235 |
24 245 |
24,5 250 |
- |
- |
- |
- |
|
Б - естественного твердения |
20 201 |
21,5 219 |
23 235 |
- |
- |
- |
- |
- |
- |
|
подвергнутый тепловой обработке при атмосферном давлении |
17,5 178 |
19 191 |
20,5 209 |
- |
- |
- |
- |
- |
- |
|
В - подвергнутый автоклавной обработке |
18 181 |
19,5 190 |
21 214 |
22 224 |
23 235 |
23,5 240 |
21 245 |
24,5 250 |
25 255 |
|
Примечания: 1. Над чертой указаны значения в МПа, под чертой - в кгс/см2. 2. Группы мелкозернистого бетона приведены в п. 2.2. 3. Для напрягающего бетона значения Eb принимают, как для тяжелого бетона, с умножением на коэффициент α = 0,56 + 0,006 В. |
|||||||||
АРМАТУРА
2.15 (2.14). Для армирования армоцементных конструкций необходимо применять:
а) тканые сетки по ГОСТ 3826-82;
б) плетеные сетки по ГОСТ 2715-75*;
в) тарные сетки по ТУ 14-4-713-76;
г) стержневую и проволочную арматуру в соответствии с указаниями СНиП 2.03.01-84.
2.16 (2.15). Рекомендуемый сортамент тканых и сварных сеток приведен в табл. 1 прил. 1.
Примечание. Плетеные сети по ГОСТ 2715-75* допускается применять в качестве конструктивной арматуры.
2.17 (2.16). Выбор стержневой и проволочной арматуры в зависимости от типа конструкции, наличия предварительного напряжения, условий воздействия и эксплуатации, а также выбор марок стали для закладных деталей следует производить в соответствии с указаниями СНиП 2.03.01-84.
НОРМАТИВНЫЕ И РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ АРМАТУРЫ
2.18 (2.17). Нормативные сопротивления стержневой и проволочной арматуры Rsn, а также коэффициенты условий работы арматуры должны приниматься согласно СНиП 2.03.01-84.
Расчетные сопротивления арматуры растяжению Rs для предельных состояний первой и второй групп следует принимать согласно СНиП 2.03.01-84. Расчетные сопротивления стержневой и проволочной арматуры сжатию, используемые при расчете армоцементных конструкций по предельным состояниям первой группы Rsc, принимаются равными соответствующим расчетным сопротивлениям арматуры растяжению Rs, но не более 390 МПа.
2.21 (2.18). За нормативное сопротивление проволоки сеток принимается наименьшее значение условного предела текучести, соответствующего остаточному относительному удлинению 0,2 % и принимаемого равным 0,8 временного сопротивления разрыву проволоки сеток. Допускается нормативное сопротивление проволок тканых и сварных сеток Rm, ser принимать равным 245 МПа (2500 кгс/см).
2.22 (2.19). Расчетное сопротивление сеток растяжению для предельных состояний первой и второй групп определяется делением нормативного сопротивления на коэффициент безопасности по материалу сеток, равный для предельных состояний первой группы 1,1.
2.23. Значения расчетных сопротивлений сеток растяжению для предельных состояний первой группы Rm и Rmω, а также сжатию Rmc, с учетом коэффициента условий работы 1,1, следует принимать по табл. 11, используемых при расчете по предельным состояниям первой группы.
Расчетное сопротивление сеток сжатию, используемое при расчете конструкций по предельным состояниям первой группы Rmc, принимается равным расчетному сопротивлению растяжения для предельных состояний первой группы Rm.
Расчетное сопротивление сеток сжатию Rmc, приведенное в табл. 11, необходимо дополнительно умножать на коэффициент условия работы сеток γm2, принимаемый в зависимости от коэффициента сетчатого армирования сжатой зоны элемента по табл. 12.
2.24 (2.21). Расчетное сопротивление сеток в элементах, подвергающихся воздействию многократно повторяющихся нагрузок, следует принимать с коэффициентом условий работы по СНиП 2.03.01-84 как для арматуры класса А-II.
2.25 (2.22). Модуль упругости сеток Em следует принимать равным 150000 МПа (1500000 кгс/см2), а модуль упругости стержневой и проволочной арматуры Es - согласно требованиям СНиП 2.03.01-84.
Таблица 11
|
Расчетные сопротивления сеток для предельных состояний первой группы |
||||
|
Диаметр проволоки, мм |
растяжению |
сжатию R'mc |
||
|
продольных проволок; поперечных проволок при расчете наклонных сечений на действие изгибающего момента Rm |
поперечных проволок при расчете наклонных сечений на действие поперечной силы Rmω |
|||
|
Тканая по ГОСТ 3826-82 * |
0,7 |
|
|
|
|
1 |
|
|
|
|
|
1,1 |
|
|
|
|
|
1,2 |
245 2500 |
206 2100 |
245 2500 |
|
|
Сварная по ТУ 14-4-713-76 |
0,5 |
|
|
|
|
Примечание. Над чертой указаны значения в МПа, под чертой - в кгс/см2. |
||||
Таблица 12
|
Коэффициент γm2 |
|
|
Менее 0,015 |
1 |
|
0,015 - 0,025 |
0,75 |
2.26 (2.23). Длину зоны передачи напряжения lp для напрягаемой арматуры без анкеров следует определять согласно указаниям СНиП. 2.03.01-84.
3. РАСЧЕТ АРМОЦЕМЕНТНЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
3.1 (3.1). Расчет элементов армоцементных конструкций по прочности должен производиться для сечений, нормальных к продольной оси, а также для наклонных к ней сечений наиболее опасного направления. Кроме того, необходимо выполнить расчет указанных элементов на местное действие нагрузки (смятие и продавливание).
Расчет элементов армоцементных конструкций на местное действие нагрузки следует производить в соответствии с требованиями СНиП 2.03.01-84.
3.2 (3.2). Сетки, а также ненапрягаемую и напрягаемую стержневую или продольную арматуру, если расстояние между стержнями арматуры не превышает 10t (t - толщина рассматриваемого сечения), при расчете по прочности сечений армоцементных конструкций следует принимать равномерно распределенными по сечению элемента с коэффициентом приведенного армирования, определяемым по формулам:
для растянутой зоны
μm1 = μm + μsRs/Rm + μspRsp/Rm; (3)
для сжатой зоны
μ'm1 = μ'm + μ'sRsc/Rmc + μ'spRspc/Rmc, (4)
где μm, μ'm - коэффициенты сетчатого армирования, равные:
μm = Am/t; μ'm = A'm/t, (5)
μs, μ's - коэффициенты армирования стержневой и проволочной арматурой, равные:
μs = As1/A; μ's = A's1/A, (6)
μsp, μ'sp - коэффициенты армирования преднапряженной арматурой:
μsp = Ap1/A; μ'sp1 = A'sp1/A, (7)
Am, A'm - площади сечения сеток на единицу длины соответственно в растянутой и сжатой зонах; As1, A's1 - площади сечения ненапрягаемой стержневой арматуры на данном участке поперечного сечения элемента соответственно в растянутой и сжатой зонах; Rs, Rsp - расчетные сопротивления арматуры соответственно обычной и преднапряженной растяжению; Asp1, A'sp1 - площади сечения напрягаемой арматуры соответственно в растянутой и сжатой зонах; Rsc, Rspc - расчетные сопротивления арматуры соответственно обычной и преднапряженной сжатию; A - площадь поперечного сечения на данном участке; t - толщина элемента на рассматриваемом участке сечения.
На участках сечения, где расстояния между арматурными стержнями свыше 10t, усилия в стержневой и проволочной арматуре должны учитываться для каждого стержня раздельно.
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
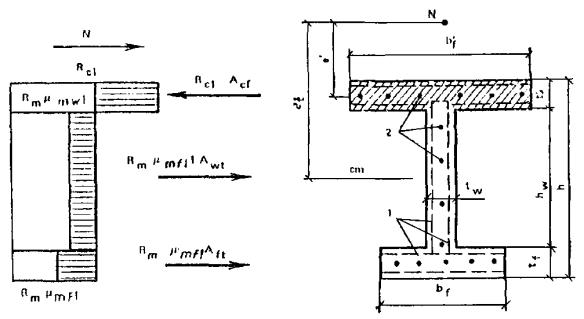
3.3 (3.3). Предельные усилия в сечении, нормальном к продольной оси элемента, определяются исходя из следующих предпосылок (рис. 17):
Рис. 17. Схема внутренних усилий и эпюра напряжений в сечении, нормальном к продольной оси элемента, при расчете на прочность
1 - сетки; 2 - стержневая или проволочная арматура, приведенная к равномерному распределению по сечению элемента; 3 - сосредоточенная стержневая и проволочная арматура
сопротивление бетона растяжению принимается равным нулю;
сопротивление бетона сжатию выражается напряжениями, равными Rb, равномерно распределенными по сжатой зоне бетона;
напряжения в арматуре, расположенной в сжатой зоне бетона, принимаются постоянными и не более Rmc, Rsc, Rpc;
растягивающие напряжения в арматуре принимаются постоянными по высоте растянутой зоны сечения и не более Rm, Rs, Rsp.
3.4 (3.1). Расчет сечений, нормальных к продольной оси элемента, когда внешняя сила действует в плоскости оси симметрии, должен производиться в зависимости от значения относительной высоты сжатой зоны бетона ξ = x/h, определяемого из условия равновесия и граничного значения относительной высоты сжатой зоны бетона ξR, при котором предельное состояние элемента наступает одновременно с достижением в растянутых сетках и в стержневой или проволочной арматуре напряжений, равных расчетным сопротивлениям.
3.5. Значение ξR определяется по формуле
где ω - характеристика сжатой зоны бетона, определяемая для армоцементных конструкций мелкозернистого бетона по формуле
ω = 0,7 - 0,008Rb. (9)
Характеристику сжатой зоны мелкозернистого бетона ω для внецентренно сжатых армоцементных элементов с толщиной полки менее 0,04 м следует принимать
ω = 0,5 - 0,008Rb,
Rb - принимается в МПа; σs - напряжение в арматуре, МПа, принимаемое равным: для сеток Rm; для стержневой и проволочной арматуры классов: А-I, А-II, А-III, А-IIIв, Вр-I - (Rs - σsp); А-IV, А-V, А-VI, В-II, Вр-II, К-7 и К-19 - (Rs + 400 - σsp - Δσsp); В-II, Вр-II, К-7, К-19 - (Rs + 400 - σsp); Rs - расчетное сопротивление растяжению стержневой и проволочной арматуры с учетом соответствующих коэффициентов условий работы арматуры γsi принимается по СНиП 2.03.01-84; σsp - определяется при коэффициенте γp < 1 согласно указаниям СНиП 2.03.01-84; Δσsp - принимается по СНиП 2.03.01-84; σsc, u - предельное напряжение в арматуре сжатой зоны, принимаемое при γb1 ≥ 1 (см поз. 1 табл. 9) равным 400 МПа, а для элементов из мелкозернистого бетона, если учитывается коэффициент γb1 < 1 - равным 500 МПа. При расчете элементов в стадии обжатия значение σsc, u принимается равным 330 МПа.
3.6 (3.6). Для напрягаемой арматуры, имеющей сцепление с бетоном и расположенной в зоне, сжатой от действия внешних усилий, расчетное сопротивление арматуры сжатию Rsc должно быть заменено напряжением σsc согласно СНиП 2.03.01-84.
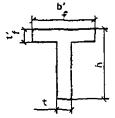
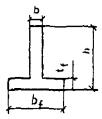
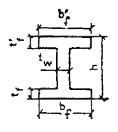
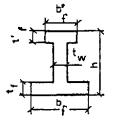
ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ ПРЯМОУГОЛЬНОГО, ТАВРОВОГО, ДВУТАВРОВОГО И КОЛЬЦЕВОГО СЕЧЕНИЙ
3.7. Расчет прямоугольных сечений с арматурой, приведенной к равномерно распределенной по сечению элемента (см. п. 3.2), когда внешняя сила действует в плоскости оси симметрии сечения (рис. 18) при ξ = x/h < ξR, должен производиться из условия
M ≤ Rmμm1Ath/2, (10)
при этом высота сжатой зоны x определяется по формуле
x = Rmμmh/(Rc1 + Rmμm1), (11)
где At = (h - x)b,
Rc1 = Rb + μ'm1Rcm, (12)
μm1 - принимается согласно п. 3.1.
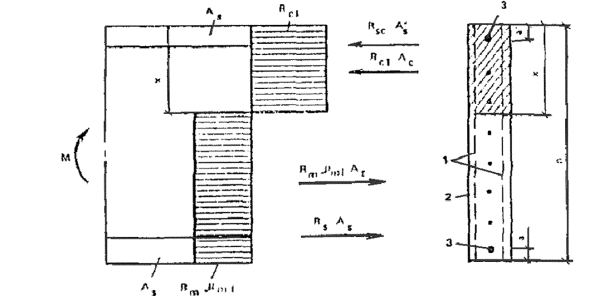
3.8. Расчет прямоугольных сечений, в которых наряду с арматурой, приведенной к равномерно распределенной (см. п. 3.2), имеется стержневая и проволочная арматура, сосредоточенная у растянутой и сжатой граней сечения (рис. 19), при ξ = x/h ≤ ξR должен производиться из условия
M ≤ Rc1Ac(h - x/2 - a) - RscA'c(h - a - a') - Rmμm1At[(h - x)/2 - a], (13)
где Ac = xb,
при этом высота сжатой зоны бетона определяется по формуле
x = (Rmμm1At - RscA'c + RsAs)/[(Rc1 + Rmμ'm1)b], (14)
где Rc1 = Rb + Rmcμ'm1;
At = (h - x)b,
μm1 - принимается согласно п. 3.2.
3.9. Расчет двутавровых сечений с арматурой, приведенной к равномерно распределенной (см. п. 32), имеющих полку в сжатой зоне, при ξ = x/h £ ξR должен производиться в зависимости от положения границы сжатой зоны бетона:
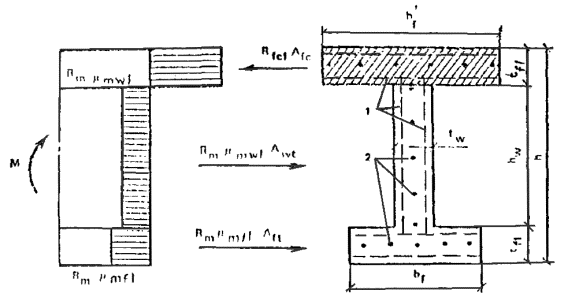
а) если граница сжатой зоны проходит в полке (рис. 20), т.е. соблюдается условие
Rc1Afc ≥ Rmμmf1Af + Rmμmω1Aωt, (15)
расчет должен производиться по формуле
M ≤ Rmμmf1Aft[h - (tf + t'f)/2] + Rmμmω1Aω(hω + t'f)/2; (16)
б) если граница сжатой зоны проходит в ребре (рис. 21), т.е. условие (15) не соблюдается, расчет производится по формуле
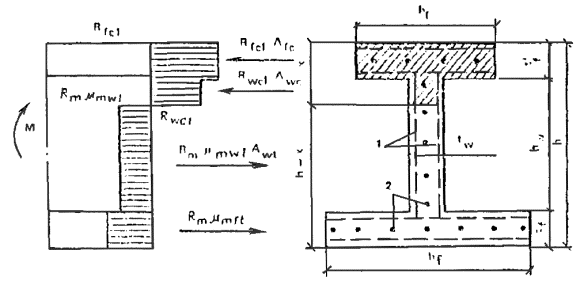
M ≤ Rcf1Afc[h - (tf + t'f)/2] + Rcω1Aωc[h - (x + tf)/2] - Rmμmω1Aωt(h - x)/2. (17)
Высота сжатой зоны x определяется из условия
Rcf1Afc + Rcω1Aωc = Rmμmf1At + Rmμmω1Amωt. (18)
Rcf1 = Rb + Rmcμmf1;
Rcω1 = Rb + Rmcμmω1; Afc = b'ft'f;
Aft = bftf; Aω = tωhω;
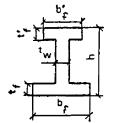
Aωc = (x - t'f)tω; Aωt = (h - x - tf)tω.
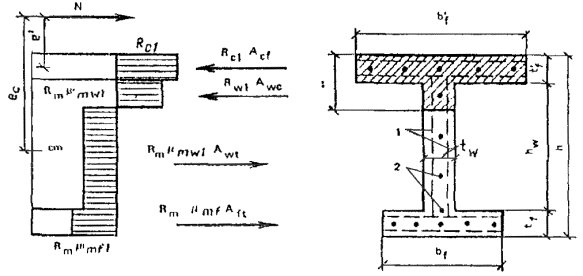
Коэффициент приведенного армирования стенки μmω1 сжатой полки μ'mf1 и растянутой полки μmf1 принимаются в соответствии с п. 3.2.
3.10. Расчет тавровых сечений с полкой в сжатой зоне или приведенных к тавровым сечениям, в которых наряду с арматурой, приведенной к равномерно распределенной, имеется стержневая или проволочная арматура в растянутой зоне, при ξ = x/h ≤ ξR следует выполнять в зависимости от высоты сжатой зоны бетона:
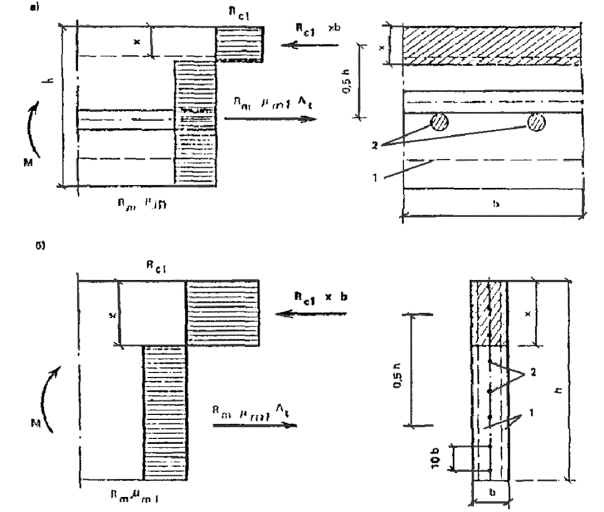
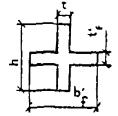
Рис. 18. Схема усилий и эпюра напряжений в изгибаемых элементах прямоугольного сечения
а - при b > h; б - при b < h; 1 - сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению элемента
Рис. 19. Схема усилий и эпюра напряжений в изгибаемых элементах прямоугольного сечения с сосредоточенной стержневой и проволочной арматурой
1 - сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению элемента; 3 - сосредоточенная стержневая или проволочная арматура
Рис. 20. Схема усилий и эпюра напряжений в изгибаемых элементах двутаврового сечения при x ≤ t'f
1 - сетки; 2 - стержневая и проволочная арматура, приведенная к равномерно распределенной по сечению
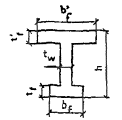
Рис. 21. Схема усилий и эпюра напряжений в изгибаемых элементах двутаврового сечения при x > t'f
1 - тонкие сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению
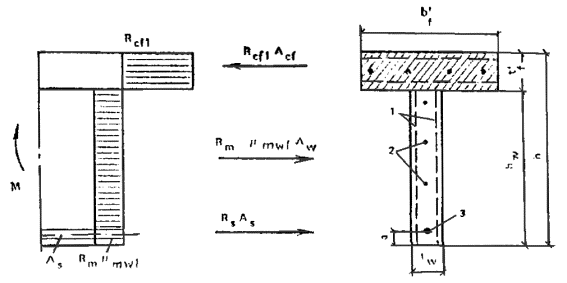
а) если сжатая зона находится в пределах полки (рис. 22), т.е. соблюдается условие
Rcf1Acf ≥ Rmμmω1Aω + RsAs (19)
прочность сечения определяется из условия
M ≤ Rmμmω1Aω(hω + t'f)/2 + RsAs(h - t'f/2 - a); (20)
Рис. 22. Схема усилий и эпюра напряжений в изгибаемых элементах таврового сечения с полкой в сжатой зоне при x ≤ t'f
1 - тонкие сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению элемента; 3 - сосредоточенная стержневая или проволочная арматура
Рис. 23. Схема усилий и эпюра напряжений в изгибаемых элементах таврового сечения с полкой в сжатой зоне при x > t'f
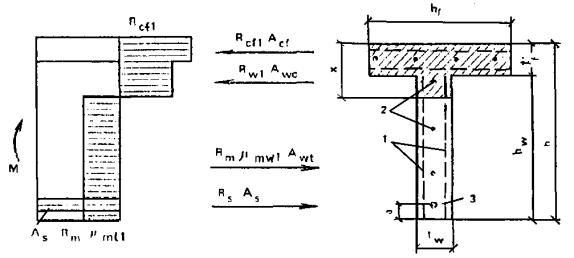
1 - тонкие сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению элемента; 3 - сосредоточенная стержневая или проволочная арматура
б) если граница сжатой зоны выходит за пределы полки (рис. 23), т.е. условие (19) не выполняется, прочность сечения определяется из условия
M ≤ Rcf1Acf[h - t'f/2 - a] + Rcω1Acω[h - (x + t'f)/2 + a] - Rmμmω1Aωt[(h - x)/2 - a], (21)
при этом высота сжатой зоны x определяется из условия
Rcf1Acf + Rω1Aωc = Rmμmω1Aωt + RsAs. (22)
Rcω1 = Rb + Rmcμmω1;
Afc = b'ft'f; Aω = tωhω;
Aωc = (x - t'f)tω;
Aωt = (h - x)tω.
Коэффициенты приведенного армирования сжатой полки μ'mf1, μmf1, μmω1 принимаются согласно п. 3.2.
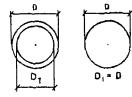
Рис. 24. Схема кольцевого сечения, принимаемая в расчете по прочности армоцементных элементов
3.11 (3.11). Ширина сжатой полки b'f тавровых и двутавровых сечений, вводимая в расчет в соответствии с пп. 3.9 и 3.10, принимается из условия, что ширина свободного свеса в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
а) 1/2 расстояния в свету между продольными ребрами при наличии поперечных ребер;
б) t'f при отсутствии поперечных ребер или при расстоянии между ними большими, чем расстояние между продольными ребрами, при t'f ≤ 0,1h;
в) 6t'f1 при t'f ≥ 0,1h;
3t'f при 0,05tf < t'f < 0,1h.
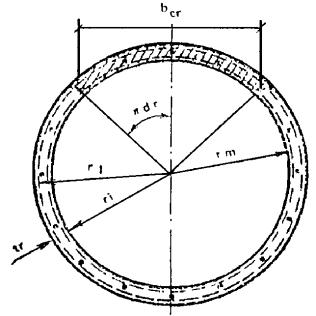
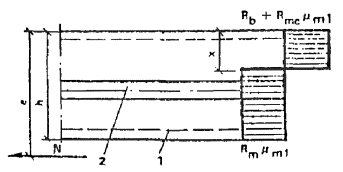
3.12 (3.12). Расчет кольцевых сечений (рис. 24) должен производиться:
а) при Rmμmr1 > 0,38Rcr1
из условия
где Rcr1 = Rb + Rmcμmr1; Ar = 2πrmtω;
αr = Rmμmr1/(Rb + 3,35Rmμmr1), (24)
здесь rm - радиус срединной поверхности стенки кольцевого элемента, равный:
rm = (ri + re)/2, (25)
re, ri - радиусы соответственно наружной и внутренней граней кольцевого сечения;
μmr1 - коэффициент приведенного армирования кольцевого сечения, определяемый в соответствии с п. 3.3;
б) при Rmμmr1 < 0,38Rcr1
из условия
αr = 0,73Rmμmr1/(Rb + 2Rmμmr1); (27)
Rcr1 = Rb + R'mcμ'mr1. (28)
3.13 (3.13). При расчете по прочности изгибаемых элементов армоцементных конструкций рекомендуется соблюдать условие x ≤ ξRh.
В случае когда площадь сечения растянутой арматуры по конструктивным соображениям или из расчета по продельным состояниям второй группы принята большей, чем это требуется для соблюдения условия x ≤ ξRh, расчет следует производить по формулам (10), (13), (17), (20), (21), принимая x = ξRh.
ПРИМЕРЫ РАСЧЕТА
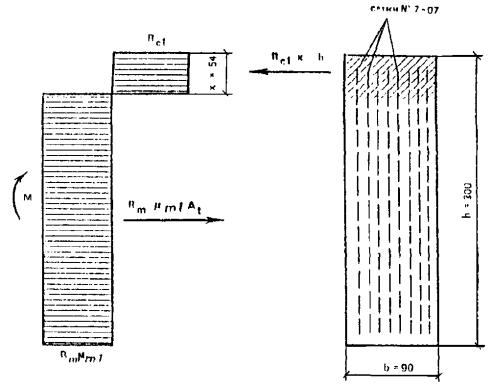
Пример 1.
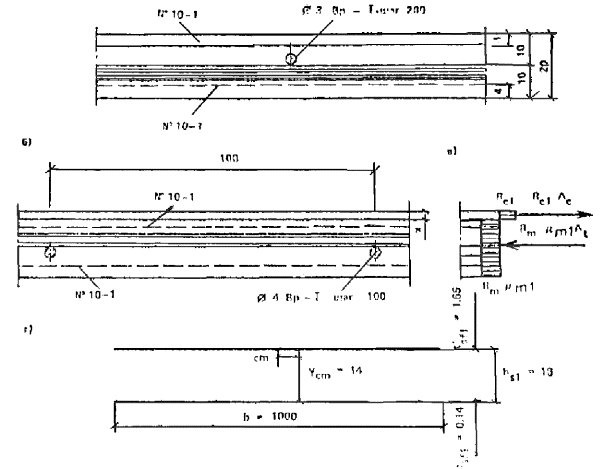
Дано. Прямоугольное сечение армоцементного элемента (рис. 25) с размерами h = 300 мм и b = 90 мм находится под действием изгибающего момента M = 0,3 кН×м. Элемент выполнен из бетона класса В20 и армируется ткаными сетками № 7-07 по ГОСТ 3826-82* в количестве восьми слоев, равномерно распределенных по сечению.
Требуется проверить прочность нормального течения.
Рис. 25. Схема усилий и эпюра приведенных напряжений в изгибаемом элементе прямоугольного сечения, армированного ткаными сетками
Расчет. В соответствии с п. 3.2 и данным табл. 1 прил. 1 определяем коэффициент сетчатого армирования μ при одной сетке на 1 см толщины сечения элемента μ = 0,0050; тогда коэффициент армирования элемента при восьми слоях сетки будет μm = 8μ/b = 8×0,0050/9 = 0,004.
В соответствии с п. 3.7 прочность прямоугольного сечения с арматурой, приведенной к равномерно распределенной по сечению, проверяем по условию (10), а высоту сжатой зоны определяем по формуле (11)
x = Rmμm1h/(Rc1 + Rmμm1),
где Rm = 245 МПа (табл. 11); Rb = 10,5 МПа (табл. 7) при γb1 = 0,9 (табл. 9)
по зависимости (12)
Rc1 = Rb + μmRmc = 10,5 + 0,004×245 = 11,18 МПа.
Тогда x = 245×0,004×30/(11,48 + 245×0,004) = 2,4 см. Прочность сечения определяем из условия (10)
M ≤ RmμmAth/2,
где At = (h - x)b = (300 - 24)90 = 24840 мм2, тогда M ≤ 245×0,004×24840×300/2 = 365148 Н×мм.
Прочность элемента обеспечена, так как M = 0,365 кН×м > 0,3 кН×м. Проверяем условие ξ = x/h ≤ ξR.
По формуле (8)
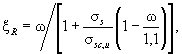
где по формуле (9) ω = 0,7 - 0,008Rb = 0,7 - 0,008×10,35 = 0,617, тогда ξR = 0,617/[1 + 245/500(1 - 0,617/1,1)] = 0,507.
Предельное отношение высоты сжатой зоны будет равно:
ξ = 2,4/300 = 0,08 < 0,507.
Условие удовлетворяется.
Пример 2.
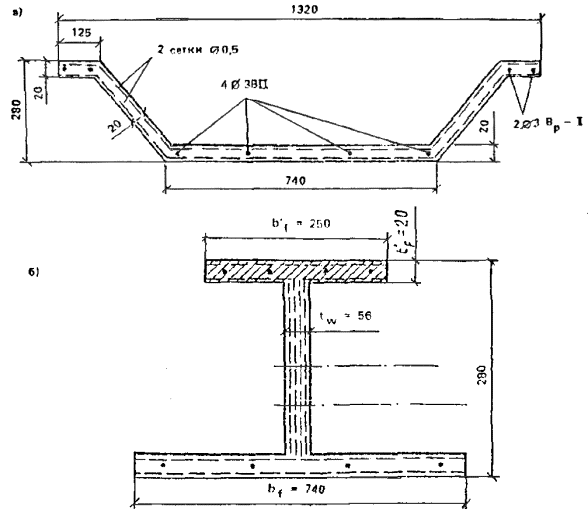
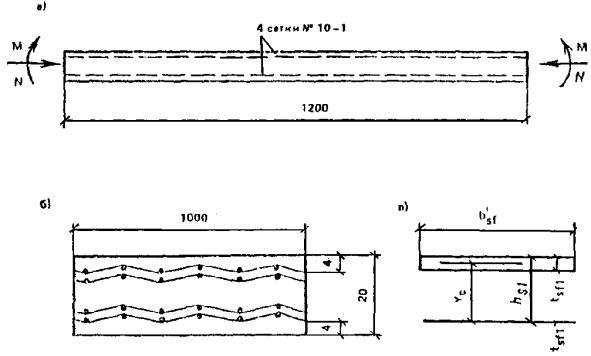
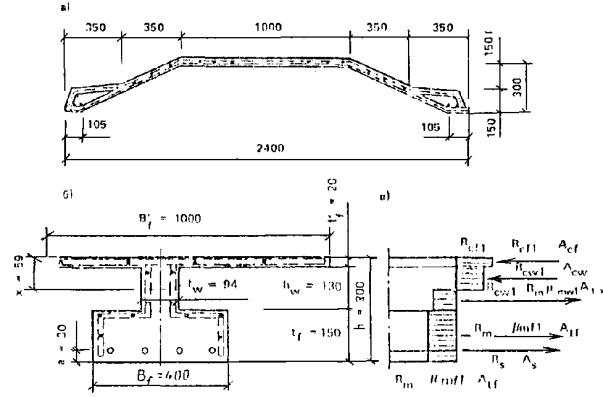
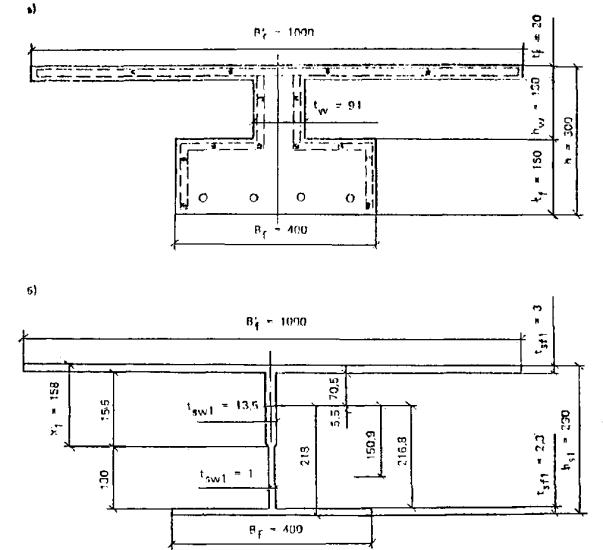
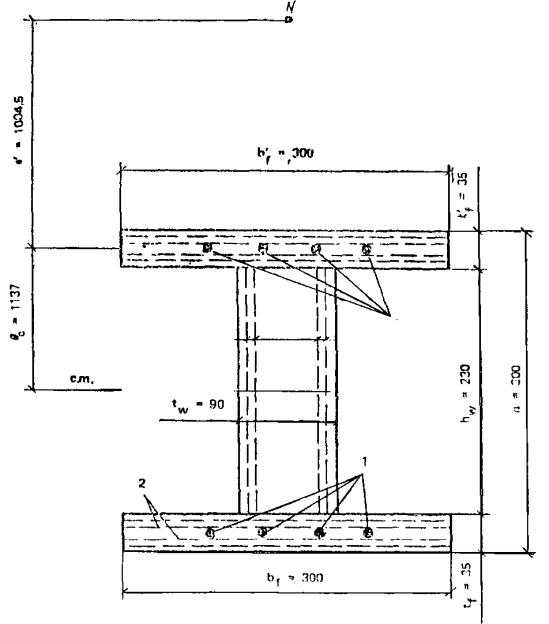
Дано. Поперечное сечение армоцементной складчатой панели (рис. 26), изгибающий момент M = 12,56 кН×м. Приведенное сечение складки приведено на рис. 26, б.
Панель изготовлена из мелкозернистого бетона класса В40. Прочность бетона панели Rb = 22 МПа. Складчатая панель армируется:
двумя слоями сварных сеток для армоцемента № 12,5-0,5 по ТУ 14-4-713-76; коэффициент армирования при толщине стенки 20 мм μm = 0,0014;
ненапрягаемой арматурой в виде стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I диаметром 3 мм (As = 4×0,0707 = 0,2828 см2);
напрягаемой арматурой из высокопрочной проволоки Вр-II диаметром 4 мм (Asp = 4×12,56 = 50,24 мм2).
Расчетные и нормативные характеристики:
сварной сетки для армоцемента Rm = 245 МПа - табл. 11;
мелкозернистого бетона Rb = 22 МПа - табл. 7;
сварных сеток из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I, по СНиП 2.03.01-84 Rs = 375 МПа;
высокопрочной проволоки класса Вр-II Rs = 1180 МПа.
Требуется проверить прочность приведенного двутаврового сечения, нормального к продольной оси.
Расчет производится в зависимости от относительной высоты сжатой зоны бетона ξ = x/h.
Рис. 26. Сечение предварительно напряженной складчатой армоцементной панели покрытия
а - сечение панели; б - расчетное сечение
Определяем граничное значение относительной высоты сжатой зоны бетона по формуле (8)
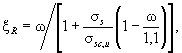
где ω - характеристика сжатой зоны бетона, определяется для армоцементных конструкций из мелкозернистого бетона по формуле (9):
ω = 0,7 - 0,008Rb = 0,7 - 0,008×22 = 0,524.
Значение предварительного напряжения в проволочной арматуре Вр-II принимаем σsp = 1062 МПа, тогда σs = 1180 + 400 - 1062 = 518 МПа, а σsc, u принимаем по СНиП 2.03.01-84 равным 500 МПа. После подстановки
ξR = 0,524/[1 + 518/500(1 - 0,524/1,1)] = 0,524/1,545 = 0,34.
Определяем коэффициенты армирования:
сжатой полки сварными сетками и стальной низкоуглеродистой холоднотянутой проволоки
μ'st = Ast/(t'fb'f) = 28,28 : 250 : 20 = 0,00566;
растянутой полки - высокопрочной проволокой
μs = 50,24/(740×20) = 0,0038.
В соответствии с п. 3.2 определяем коэффициенты приведенного армирования:
верхний (сжатой) полки
μ'mf1 = μm + μsRsc/Rmc = 0,0014 + 0,00566×375 : 245 = 0,01;
растянутой полки
μmf1 = μm + μpRps/Rmc = 0,0014 + 0,0038×1180 : 245 = 0,0197;
Приведенная толщина вертикальной сетки tω = t/sin 45° = 20×2/0,7 = 56 мм.
μmω1 = 0,0014.
Для определения положения нейтральной оси проверяем условие (15):
Rc1Acf > Rmμmf1Aft + Rmμmω1Aωt;
Rc1Acf = (22 + 245×0,01)250×20 = 122500 Н > Rmμmf1Aft + Rmμmω1Aωt = 245×0,0014×240×56 + 245×0,0197×20×740 = 117495,1 Н.
Так как 122500 > 117495,1, условие (15) соблюдается, нейтральная ось проходит в пределах верхней полки.
Принимая x = t'f, условие предельной высоты сжатой зоны также выполняется, так как
ξ = x/h = 20/280 = 0,07 и ξR = 0,33.
Пользуясь формулой (16), определяем несущую способность сечения
M ≤ Rmμmf1Aft[h - (tf + t'f)/2] + Rmμmω1Aω(hω + t'f)/2 = 245×0,0197×740×20[280 - (20 + 20) : 2] + 245×0,0014×56×240(240 + 20) : 2 = 19,122 кН×м.
Mp = 12,56 кН×м < M = 19,122 кН×м. Прочность нормального сечения складчатой панели обеспечена.
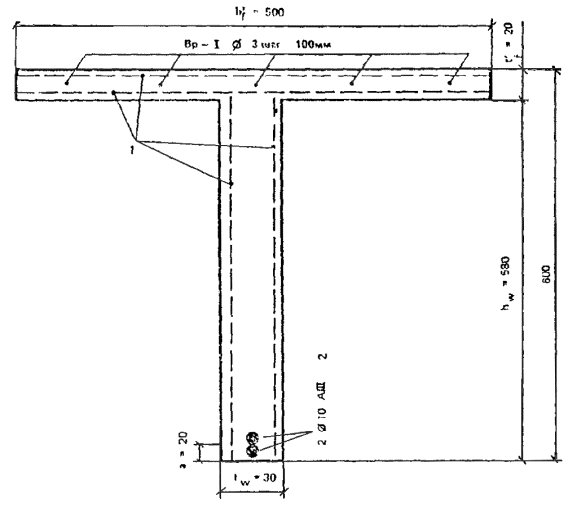
Пример 3.
Дано. Элемент таврового сечения с размерами b'f = 250 мм; t'f = 20 мм; tω = 30 мм; a = 20 мм; h = 600 мм (рис. 27). Бетон мелкозернистый класса В40 (Rb = 19,8 МПа).
Арматура: две тканые сетки № 10-1 ГОСТ 3826-82*; стержневая арматура класса Вр-I; Æ = 3 мм; Rs = 375 МПа; шаг - 100 мм; сосредоточенная стержневая арматура класса A-III; Rs = 365 МПа; два стержня диаметром 10 мм. Изгибающий момент M = 50 кН×м.
Требуется проверить прочность сечения.
Рис. 27. Сечение таврового элемента
1 - сетки № 12,5 по ТУ 14-4-713-76; 2 - стержневая арматура класса А-III
Расчет. Проверку прочности сечения производим согласно п. 3.10 из выражения (19)
Rcf1Acf ≥ Rmμmω1Aω + RsAs.
Определяем, проходит ли нейтральная ось в полке или в стенке. Определяем коэффициенты приведенного армирования согласно (п. 3.2). Коэффициенты армирования стержневой арматурой равны:
μs = As/Abf = 7,068 : (20×100) = 0,0035;
μsω = As/Abω = 7,068 : (30×100) = 0,0024.
Коэффициенты армирования, пользуясь данными табл. 1 прил. 1, при двух сетках в полке толщиной 20 мм равны: μmf = 0,0071 и в двух сетках в стенке толщиной 30 мм μmω = 0,0047.
Тогда приведенные коэффициенты армирования:
μmf1 = μmf + μsRs/Rm = 0,0071 + 0,0035×365 : 245 = 0,0123;
μmω1 = μmω + μsωRs/Rm = 0,0047 + 0,0024×365 : 245 = 0,0083.
Приведенная прочность сжатой полки
Rcf1 = Rb + Rmcμmf1 = 19,8 + 245×0,0123 = 22,313.
Сечение сжатой полки равно:
Acf = b'ft'f = 250×20 = 5000 мм2,
а вертикальной стенки равно:
Aω = tωhω = 580×30 = 17400 мм2.
Площадь стержневой арматуры
As = 2×78,50 = 157 мм2.
После подстановки полученных величин в выражение (19) получаем 22,813×5000 > 245×0,0123×17400 + 365×15700, т.е. граница сжатой зоны пересекает вертикальную стенку.
Прочность сечения определяем из выражения (21)
M ≤ Rcf1Acf[h - t'f/2 - a] + Rcω1Aωchω - (x - 2a + t'f)/2 - Rmμmω1Aωt[(h - x)/2 - a].
Определяем приведенную прочность сжатой части стенки
Rcω1 = Rb + Rmcμmω1 = 19,8 + 245×0,0083 = 21,83 МПа.
Высоту сжатой зоны x определяем из условия (22)
Rcf1Afc + Rcω1Aωc = Rmμmω1Aωt + RsAs.
После подстановки
22,813×5000 + 21,82×30x = 245×0,0083(17400 - 30x) + 365×157.
Тогда x = 47,1 мм, а отношение к высоте сечения
ξ = x/h = 47,1/600 = 0,079; ξ < ξR = 0,37.
Выполняя подстановку полученных величин в выражение (21), получаем
M = 22,83×5000(600 - 20/2 - 20) + 21,813×27,1[580 - (47,1 - 2×20 + 20)/2] - 245×0,0083×17400[(600 - 47,1)/2 - 20]10-6 = 56,165 кН×м.
Поскольку расчетный изгибающий момент в сечении превышает внешний изгибающий момент M = 56,2 кН×м > 50 кН×м, прочность сечения обеспечена.
Пример 4.
Дано. Элемент двутаврового сечения с размерами b'f = 800 мм; t'f = 20 мм; h = 300 мм; tω = 40 мм; tf = 20 мм; bf = 1000 мм; бетон мелкозернистый класса В25 (при γb1 = 0,9, Rb = 13,05 МПа); арматура класса Вр-I; Æ = 5 мм; шаг - 150 мм; Rs = 360 МПа; сетка тканая № 10-1; Rm = 245 МПа; коэффициент сетчатого армирования при одной сетке на 1 см μm = 0,0071. Изгибающий момент M = 9 кН×м. Требуется проверить прочность сечения.
Расчет. Расчет ведем согласно указаниям п. 3.9. Предварительно согласно п. 3.2 определяем коэффициент приведенного армирования
μm1 = μm + μsRs/Rm,
где коэффициент армирования проволочной арматурой верхней и нижней полки
μs = As/Ab = 19,63 : (20×150) = 0,00654.
Коэффициент армирования проволочной арматурой стенки
μs = As/Ab = 19,53 : (40×150) = 0,0033.
Тогда:
μ'm1 = μ'm + μ'sRs/Rm = 0,0071 + 0,00654×360 : 245 = 0,0167;
μmω1 = μm + μsRs/Rm = 0,0071×0,5 + 0,0033×360 : 245 = 0,0083;
μmf1 = μm + μsRs/Rm = 0,0071 + 0,00654×360 : 245 = 0,0167.
Определяем предельное отношение высоты сжатой зоны из выражения (8)
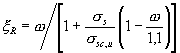 .
.
Для мелкозернистого бетона из выражения (9):
ωn = 0,7 - 0,008Rb = 0,7 - 0,008×13,05 = 0,596;
ξR = 0,596/[1 + 360/500(1 - 0,596/1,1)] = 0,448.
Высоту сжатой зоны x определяем из условия (18)
Rcf1Afc + Rcω1Aωc = Rmμmf1Aft + Rmμmω1Aωt.
Вычислим величины, входящие в это выражение с использованием п. 3.9:
Rcf1 = Rb + Rmcμmf1 = 13,05 + 245×0,0167 = 16,92 МПа;
Rcω1 = Rb + Rmcμmω1 = 13,05 + 245×0,083 = 15,08 МПа;
Acf = b'ft'f = 800×20 = 1600 мм2;
Aft = bftf = 1000×20 = 20000 мм2;
Aω = hωfω = (300 - 20 - 20)40 = 10400 мм2;
Aωc = (x - t'f)tω = (x - 20)40 = 40x - 800;
Aωt = (h - x - tf)tω = (300 - x - 20)40 = 12000 - 40x - 800 = 11200 - 40x.
Полученные величины подставляем в выражение (18):
16,92×1600 + 15,08(40x - 800) = 245×0,0167×20000 + 245×0,0083(11200 - 40x).
Высота сжатой зоны x = 131 мм. Проверяем отношение ξ = 0,44 < ξR = 0,448. Граница сжатой зоны проходит в ребре двутаврового сечения, и в соответствии с п. 3.9 прочность сечения определяем по формуле (17)
M ≤ Rcf1Afc[h - (tf + t'f)/2] + Rcω1Aωc[h - (x + tf)/2] - Rmμω1Aωt(h - x)/2;
после подстановки
M ≤ 16,92×1600[300 - (20 + 20)/2] + 15,08×4440[30 - (131 + 20)/2] - 245×0,0083×5960(300 - 131)/2 = 9,60×106 Н×мм.
Так как расчетный момент в сечении M = 9,6 кН×м > M = 9 кН×м, прочность сечения обеспечена.
Дано. Элемент кольцевого сечения с наружным радиусом re = 300 мм и внутренним радиусом ri = 260 мм, бетон класса В25 (Rb = 13,05 МПа, при γb1 = 0,9), армирование равномерное по периметру двумя сетками ткаными № 10-1; Rm = 245 МПа; шаг - 100 мм; класс Вр-I; Æ = 5 мм; Rs = 360 МПа. Расчетный изгибающий момент M = 40 кН×м. Коэффициент армирования при одной сетке на 1 см μm = 0,0071. Требуется проверить прочность сечения.
Расчет. Проверяем условие Rmμmr1 < 0,38Rcr1.
Rcr1 = Rb + R'mcμ'mr1 = 13,05 + 245×0,0215 = 18,32 МПа;
μmr1 = μm + μsRs/Rm = 0,0071 + 0,00981×360 : 245 = 0,0215;
μs = As/Ab = 19,63 : (20×100) = 0,00981;
245×0,0215 < 0,38×18,32.
После подстановки 5,268 < 6,961, т.е. условие выполнено. Прочность сечения определяем из формулы (26)
![]()
αr = 0,73Rmμmr1/(Rb + 2Rmμmr1) = 0,73×245×0,0215 : (13,05 + 2×245×0,0215) = 0,163039.
Радиус срединной поверхности
rm = (ri + re)/2 = (260 + 300) : 2 = 280 мм,
площадь кольцевого сечения Ar = 2πmrmtω = 35168 мм2. Прочность кольцевого сечения
M ≤ 35168[18,32sin180×0,16304/3,14 + 0,234×245×0,0229]280 = 41050200 Н×мм.
Поскольку M = 10 кН×м < 41,05 кН×м, прочность кольцевого сечения обеспечена.
Пример 6.
Дано. Элемент кольцевого сечения с наружным радиусом rc = 300 мм и внутренним радиусом ri = 260 мм, бетоном класса В20 (Rb = 10,5 МПа при γb1 = 0,9) и с армированием, равномерно распределенным по периметру, выполненным двумя сетками № 10-1; коэффициент армирования μm = 0,0071 при одной сетке на 1 см (см. табл. 1 прил. 1); проволока класса Вр-I; Æ = 5 мм; шаг - 50 мм; Rs = 375 МПа. Расчетный изгибающий момент равен 75,5 кН×м. Требуется проверить прочность сечения.
Расчет. Проверяем условие Rmμmr1 < 0,38Rcr1. Вычисляем коэффициент армирования проволочной арматурой μs = As/Ab = 19,63/20×50 = 0,01963; приведенный коэффициент армирования
μmr1 = μm + μsRs/Rm = 0,0071 + 0,01963×375 : 245 = 0,03715.
Приведенная расчетная прочность полки на сжатие
Rcr1 = Rb + Rmcμmr1 = 10,5 + 245×0,03715 = 19,6 МПа.
После подстановки получаем 245×0,03715 < 0,38×19,6, или 9,102 > 7,448, т.е. условие выполнено. Прочность кольцевого сечения определяем по формуле (23). Из выражения (24) определяем коэффициент αr:
αr = Rmμmr1/(Rb + 3,35Rmμmr1) = 245×0,03715 : (10,5 + 3,35×245×0,03715) = 0,3064.
Из примера 5 радиус срединной поверхности кольцевого сечения rm = 280 мм, а площадь кольцевого сечения Ar = 35168 мм2.
Прочность кольцевого сечения по формуле (23)
![]() 35168[19,6(sin180×0,3064
: 3,14) + 245×0,03715(1
- 1,35×0,3064)1,6×0,3064]280
= 75674502 Н×мм.
35168[19,6(sin180×0,3064
: 3,14) + 245×0,03715(1
- 1,35×0,3064)1,6×0,3064]280
= 75674502 Н×мм.
Поскольку расчетный момент по прочности в кольцевом сечении M = 75,67 кН×м > M = 75,5 кН×м, прочность кольцевого сечения обеспечена.
ВНЕЦЕНТРЕННО СЖАТЫЕ ЭЛЕМЕНТЫ ПРЯМОУГОЛЬНОГО, ТАВРОВОГО, ДВУТАВРОВОГО И КОЛЬЦЕВОГО СЕЧЕНИЙ
3.15. При расчете внецентренно сжатых элементов необходимо учитывать случайный эксцентриситет ea, обусловленный не учтенными в расчете факторами, в том числе неоднородностью свойств бетона по сечению элемента, а также влияние прогиба на их несущую способность. Значение ea следует принимать не менее 1/600 всей длины элемента или длины его части между точками закрепления элементов, учитываемой в расчете 1/30 высоты сечения элемента.
Для элементов статически неопределимых конструкций величина эксцентриситета продольной силы относительно центра тяжести приведенного сечения e0 принимается равной эксцентриситету, полученному из статического расчета конструкции, но не менее ea.
Расчет внецентренно сжатых элементов должен производиться с учетом влияния прогиба элемента как в плоскости изгиба, так и в нормальной к ней плоскости. В последнем случае принимается, что продольная сила приложена с эксцентриситетом e0 не менее случайного эксцентриситета ea.
3.16. Влияние прогиба на величину эксцентриситета продольного усилия следует учитывать, как правило, путем расчета конструкций по деформированной схеме, принимая во внимание неупругие деформации материала и наличие трещин.
Допускается производить расчет конструкции по недеформированной схеме, учитывая влияние прогиба элемента путем умножения эксцентриситета ec на коэффициент η, определяемый по формуле
где Ncrt - условная критическая сила, определяемая для армоцементных элементов любой формы сечения из мелкозернистого бетона по формуле СНиП 2.03.01-84.
При гибкости элемента l0/r ≤ 14 (для прямоугольных сечений при l0/h < 4) допускается принимать η = 1. При гибкости элемента в пределах 14 ≤ l0/r < 35 (4 < l0/h < 10) и μ ≤ 0,025 (здесь μ = (Am + A'm + As + A's)/Ab) допускается принимать:
для прямоугольных сечений
Ncrt = 0,15EbA/(l0/h)2; (30)
для других форм сечений
Ncrt = 2EbI/l02. (31)
При гибкости l0/r > 35 (l0/h > 10) определение Ncrt следует производить по п. 3.24 СНиП 2.03.01-84. При отношении N > Ncrt следует увеличивать размеры сечения.
3.17. Расчет внецентренно сжатых элементов прямоугольного сечения с арматурой, приведенной к равномерно распределенной (см. п. 3.2, рис. 18), следует выполнять:
а) при ξ = x/h ≤ ξR из условия
Nel ≤ Rmμm1At(h - x)/2 - Rc1Ac(h - x/2), (32)
при этом высота сжатой зоны x, определяется по формуле
RbS'b + RmcS'm1 - RmSm1 = 0. (33)
el - расстояние от точки приложения продольной силы до растянутой грани сечения; Ac, At - площади сечений соответственно сжатой и растянутой зон сечения; S'b - статический момент площади сжатой зоны бетона относительно точки приложения продольной силы N; S'm1 - статический момент площади сжатой приведенной арматуры (см. п. 3.2) относительно той же точки; Sm1 - статический момент площади растянутой приведенной арматуры относительно той же точки;
б) при ξ = x/h > ξR из условия
N ≤ Nc - (Nc - Nin)[2ec/ein - (ec/ein)2], (34)
Nc - несущая способность центрально сжатого элемента, определяемого по формуле
Nc = Rc1A, (35)
здесь
Rc1 = Rb + Rmcμ'm1; A = bh,
Nin - несущая способность сечения, в котором высота сжатой зоны бетона принимается равной x = ξRh и определяется из выражения
Nin = Rc1bx - Rmμm1(h - x)b, (36)
ec - эксцентриситет продольной силы относительно центра тяжести приведенного сечения, равный eс = M/h; ein - эксцентриситет продольной расчетной силы Nin, определяемый по формуле
ein = (Rc1Sc + RmSt)/Nin, (37)
Sc = bx(1 + hμm1)(h - x)/2,
St = bxμm1(h - x)/2.
3.18. Расчет внецентренно сжатых элементов таврового и двутаврового сечений с арматурой, приведенной к равномерно распределенной (см. п. 3.2), следует производить:
а) при ξ = x/h ≤ ξR, если x ≤ t'f (рис. 28), то из условия
N'e ≤ Rmμmω1Aω(hω + tf)/2 + Rmμmf1At[h - (tf + t'f)/2], (38)
высота сжатой зоны бетона определяется по формуле (33); если x > t'f (рис. 29), то из условия
N ≤ Rc1Afс - Rс1Aωc + Rmμmω1Aωt - Rmμmf1Aft, (39)
где высота сжатой зоны определяется по формуле (33);
б) при ξ = x/h > ξR по формуле (34),
где
Ne = Rc1Afc + Rω1Aω + Rf1Aft, (40)
здесь
Rс1 = Rb + Rmcμ'm1;
Rω1 = Rb + Rmcμmω1;
Rf1 = Rb + Rmcμmf1;
при x < t'f
Nin = Rc1Abfc - Rmμmf1(Abω + Abft); (41)
при x > t'f
Nin = Rс1Abfc + Rm1Abωc - Rmμmω1Abωt - Rmμmf1Aft; (42)
ein = (S*c + S*ω + S*t)/Nin, (43)
Рис. 28. Схема усилий и эпюра напряжений во внецентренно сжатых элементах двутаврового сечения при x ≤ t'f
1 - тонкие сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению элемента
Рис. 29. Схема усилий и эпюра напряжений во внецентренно сжатых элементах двутаврового сечения при x > t'f
1 - тонкие сетки; 2 - стержневая или проволочная арматура, приведенная к равномерно распределенной по сечению элемента
здесь:
S*c = Rc1b'ft'f(h - yc - t'f/2);
S*ω = Rm1μmω1tωhω(yc - tf - hω/2);
S*t = Rm1μmf1bftf(yc - tf/2);
yc - расстояние от центра тяжести приведенного сечения до растянутой или менее сжатой грани; при x > t'f
ein = (S*c + S*ωc + S*ωt + S*t)/Nin, (44)
здесь
S*ωc = Rω1Aωc[h - yc - t'f - (x - t'f)/2); (45)
S*ωt = Rmμmω1tω(hω - x - t'f)[yc - (hω - x + t'f)/2 - tf]. (46)
Влияние прогиба элемента учитывается путем умножения значения ec на коэффициент η, вычисляемый по п. 3.16.
3.19. Высоту сжатой зоны x внецентренно сжатых сечений, определяемую по формуле (33), рекомендуется при эксцентриситете e0 ≤ 1/h вычислять, используя выражение (47) и принимая размеры сечения в см.
x = -(et
- h) ± ![]() , (47)
, (47)
где et = ec + ycm - эксцентриситет нормальной силы N относительно нижней растянутой грани; e' = et - h + t'f/2 - эксцентриситет нормальной силы N относительно центра массы сжатой полки:
γ1 = (et - h)[b'ft'f - tωt'f - tω(t'f)2/2 + b'f(t'f)2/2]; (48)
γ2 = μmωγ1 + b'ft'f(μmr1 - μmω)e';
γ3 = tωμmω(het - h2/2 - tfet + t2f/2) + bftfμmf1(et - tf/2). (49)
При этом эксцентриситет продольной силы ec силы N относительно центра массы сечения определяется с учетом прогиба элемента согласно указаниям п. 3.16.
3.20. Расчет внецентренно сжатых элементов кольцевого сечения с арматурой, равномерно распределенной по длине окружности, должен производиться из условия
при этом величина относительной площади сжатой зоны бетона определяется по формуле
αr = (N + Rmμmr1Abr)/(Rb + 3,35Rmμmr1)Abr. (51)
Если полученное из этой формулы значение αr < 0,15, в условие (50) подставляется значение αr, определяемое по формуле
αr = (N + 0,73Rmμmr1Abr)/[(Rb + 2Rmμmr1)Abr], (52)
где Rc1 = Rb + R'mμmr1.
Значение величины μmr1 определяется с использованием рекомендаций п. 3.2.
ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
3.21. Расчет центрально-растянутых элементов прямоугольного сечения с арматурой, приведенной к равномерно распределенной (см. п. 3.2), следует производить из условия
N ≤ Rmμm1bh. (53)
ВНЕЦЕНТРЕННО РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
3.22. Расчет внецентренно растянутых элементов прямоугольного сечения с арматурой, приведенной к равномерно распределенной (см. п. 3.2), следует выполнять:
Рис. 30. Эпюра напряжений во внецентренно растянутых элементах прямоугольного сечения при приложении продольной силы N в пределах ядра сечения
1 - сетки; 2 - стержневая или проволочная арматура
а) если продольная сила N приложена в пределах ядра сечения (рис. 30) - из условия
N ≤ vRmμmt1bh, (54)
где v - коэффициент снижения несущей способности при внецентренном растяжении, принимаемый равным 0,8;
б) если продольная сила N приложена между ядром сечения и наружной гранью сечения из условия (54), где v принимается равным 0,6;
в) если продольная сила N приложена за пределами сечения (рис. 31) - из условия
Ne ≤ Rmμm1b[(h - x)/2]2 - (Rb + Rmcμm1)bx2/2; (55)
Рис. 31. Эпюра напряжений во внецентренно растянутых элементах прямоугольного сечения при положении продольной силы N за пределами ядра сечения
1 - сетки; 2 - стержневая или проволочная арматура
при этом высота сжатой зоны x определяется по формуле
RbS'b + RmcS'm1 - RmSm1 = 0. (56)
Если полученное из расчета по формуле (56) значение x > ξRh, то в условие (55) подставляется значение x = ξRh.
ПРИМЕРЫ РАСЧЕТА
Пример 7.
Дано. В армоцементной плите покрытия толщиной 20 мм и пролетом 1200 мм (рис. 32) действуют от расчетной нагрузки M = 0,5 кН×м и N = 100 кН. Плита армируется четырьмя слоями тканой сетки серии № 10-1 по ГОСТ 3826-82*.
Рис. 32. Сечение армоцементной плиты покрытия
а - поперечное; б - расчетное; в - приведенное к стальному
Расчетное сопротивление и модули упругости арматуры и бетона принимаются по табл. 11 и п. 2.25: Rm = Rmc = 245 МПа; Em = 15000 МПа. Для мелкозернистого бетона класса В40 группы А расчетное сопротивление на осевое сжатие табл. 7; Rb = 22 МПа, начальный модуль упругости бетона по табл. 10; Eb = 28500 МПа.
Требуется рассчитывать по прочности прямоугольное сечение плиты армоцементной плите покрытия здания.
Расчет. Расчетная длина плиты (считая торцы плиты защемленными) равна:
l0 = 0,5; l = 0,5×1200 = 600 мм.
Эксцентриситет продольной сжимающей силы ec = M/N = 0,5/100 = 0,005 м.
Коэффициент армирования всего сечения сетками определяем в соответствии с п. 3.2 и табл. прил. 1 (при коэффициенте армирования μm = 0,0071 одной сеткой на 1 см толщины)
μm1 = μmn/t = 0,0071×4/2 = 0,0142.
Коэффициент увеличения эксцентриситета, учитывающий влияние продольного изгиба на несущую способность плиты, находим в соответствии с п. 3.16.
Коэффициент увеличения эксцентриситета η = 2,31.
Эксцентриситет с учетом коэффициента увеличения η равен e'c = 0,005×2,31×1000 = 11,55 мм.
Для определения, какой случай внецентренного сжатия имеется, определяем высоту сжатой зоны из выражения (41).
Высоту сжатой зоны из уравнения (41)
x = -(et
- t) ± ![]()
Эксцентриситет продольной силы относительно растянутой грани
et = e'c + y = 11,55 + 10 = 21,55 мм,
e' = et - h + t'f/2 = 21,55 - 20 = 1,55 мм.
Поскольку для прямоугольного сечения γ1 = 0 и γ2 = 0, определяем только коэффициент γ3.
γ3 = bμm1(tet + t2/2) = 1000×0,0142(20×21,55 - 202 : 2) = 3280,2.
Высота сжатой зоны x:
x = -(21,55
+ 20) ± ![]() = -1,55 ± 7,56 = 6,01 мм.
= -1,55 ± 7,56 = 6,01 мм.
Отношение высоты сжатой зоны ξ = x/h = 6,01/20 = 0,3. Для определения предельного отношения ξR по формуле (8) вычислим по формуле (9) ω = 0,5 - 0,008Rb = 0,5 - 0,008×22 = 0,324. Тогда
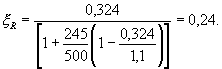
Так как ξ = x/h = 0,300 > ξR = 0,24, то согласно п. 3.17 прочность внецентренно сжатого прямоугольного сечения определяем из условия (34).
Вычислим расчетные сопротивления
Rc1 = Rb + R'mμm1 = 22 + 245×0,0142 = 25,479 МПа
и площади: Ac1 = xb = 6,01×1000 = 6010 мм2;
At = (h - x)b = (20 - 6,01)×1000 = 13990 мм2;
A = bh = 20×1000 = 20000 мм2.
Несущая способность центрально-сжатого элемента по формуле (35)
Nc = Rc1A = 25,479×20000 = 509580 Н.
Несущая способность сечения, в котором высота сжатой зоны бетона принимается равной x = ξRh, определяется из выражения (36)
Nin = Rc1bx - Rmμm1(h - x)b = 25,479×1000×6,01 - 245×0,0142(20 - 6,01)1000 = 104457,6 Н.
Эксцентриситет продольной расчетной силы Nin определяется по формуле (37)
ein = (Rc1Sc + RmSt)/Nin,
где Sc = bx(1 + hμm1)(h - x)/2 = 1000×6,01(1 + 20×0,0142)(20 - 6,01) : 2 = 53979,3 мм3;
St = bxμm1(h - x)/2 = 1000×6,01×0,0142(20 - 6,01) : 2 = 596,97 мм3;
ein = (25,479×53979,3 + 245596,97)/104457,6 = 1521588,5/104457,6 = 14,6 мм.
Прочность внецентренно сжатого прямоугольного сечения по формуле (34)
N = Nc - (Nc - Nin)[2e'c/ein - (e'c/ein)2] = 509580 - (509580 - 104457,6)[2×11,55 : 14,6 - (11,55 : 14,6)2] = 122120,4 Н = 122,12 кН.
Поскольку расчетное предельное усилие в сечении N = 122,12 кН > 100 кН, прочность армоцементной плиты обеспечена.
Пример 8.
Дано. Прямоугольное сечение армоцементной плиты толщиной 20 мм и пролетом 1200 мм, находящееся под действием длительно действующих усилий M = 300 Н×м; N = 800 Н. Кратковременно действующие усилия Me = 2 Н×м; Ne = 6 Н. Плита армируется восемью слоями тканой сетки № 10-1 - ГОСТ 3826-82*. Сетки, бетон и их расчетные сопротивления те же, что и в прим. 7. Требуется рассчитать прямоугольное сечение плиты по прочности.
Расчет. Расчетная длина плиты (считая торцы плиты защемленными) равна:
l0 = 0,5; l = 0,5×1200 = 600 мм.
Эксцентриситет продольной сжимающей силы
ec = M/N = 300000/800 = 375 мм.
Коэффициент армирования всего сечения сетками, определяемый в соответствии с п. 3.2 и табл. 1 прил. 1 (при коэффициенте армирования μm = 0,0071 одной сеткой на 1 см толщины), равен
μm1 = μmN/t = 0,0071×8 : 2 = 0,0284.
Коэффициент увеличения эксцентриситета, учитывающий влияние продольного изгиба на несущую способность плиты, находим по п. 3.16:
Ncrt = 6,4EbI/(φel20).
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в продольном состоянии, равный
φe = 1 + βMe/M,
где β - коэффициент, принимаемый в зависимости от вида бетона по табл. 30 СНиП 2.03.01-84 β = 1,3.
Тогда φe = 1 + 1,3×2/3 = 1,78. Критическая продольная сила
Ncrt = 6,4×28500×666700/1,78×6002[0,11/(0,1 + 375/20) + 0,1] = 20000 Н,
где ec/h > (0,5 - 0,01l0/h - 0,01Rb).
Коэффициент увеличения эксцентриситета
η = 1/(1 - N/Ncrt) = 1 : (1 - 800 : 20000) = 1,04.
Эксцентриситет продольной силы с учетом коэффициента увеличения η равен: e'c = ecη = 375×1,04 = 390 мм. Для определения, какой случай внецентренного сжатия имеет место, определяем высоту сжатой зоны по зависимости (33). Высоту сжатой зоны определяем из уравнения (41).
Эксцентриситет, относительно растянутой грани et = e'c + y = 390 + 10 = 400 мм. Поскольку для прямоугольного сечения γ1 = 0 и γ2 = 0, то определяем только γ3:
γ3 = bμm1(tet - t2/2) = 1000×0,0284(20×400 - 202 : 2) = 221520.
Высота сжатой зоны х
x
= -(400 - 20) ± ![]() =
-380 ± 383,95; x = 4 мм.
=
-380 ± 383,95; x = 4 мм.
Отношение высоты сжатой зоны x к толщине плиты ξ = x/h = 4/20 = 0,2 < ξR = 0,24. В соответствии с п. 3.17 при отношении ξ < ξR прочность внецентренно сжатого прямоугольного сечения определяем по формуле (32)
-Net ≤ Rmμm1At(h - x)/2 - RcAc(h - x/2) = 245×0,0284×1600(20 - 4) : 2 - 22×4000(20 - 4 : 2) = 693376 Н×мм,
где At = (h - x)b = (20 - 4)1000 = 16000 мм, Ac = xb = 4×1000 = 4000 мм2.
Расчетная продольная сила
N = Net/et = 693376/672,5 = 1031 Н = 1 кН.
Поскольку N = 1 кН > N = 0,8 кН, прочность сечения обеспечена.
Дано. Сводчатое двухшарнирное покрытие производственного здания. В нормальном к продольной оси сечении складчатого элемента действуют усилия: M = 274 кН×м (от действия постоянных и длительных нагрузок); M = 146 кН×м; N = 555 кН. Пролет свода l0 = 19,44 м. Складчатый элемент свода армируется двумя слоями тканой сетки № 10-1 ГОСТ 3826-82* и сварными плоскими каркасами из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I; Æ = 5 мм. Расчетные сопротивления арматуры и бетона, соответственно равные; для тканой сетки Rm = 245 МПа по табл. 11; для сварных каркасов из стальной низкоуглеродистой холоднотянутой проволоки по СНиП 2.03.01-84; Rs = 360 МПа; для мелкозернистого бетона класса В35 группы А; Rb = 19,5 МПа по табл. 7; начальный модуль упругости Eb = 27,5 МПа по табл. 10. Требуется рассчитать внецентренно сжатое сечение комбинированно армированного армоцементного элемента (рис. 33) по прочности.
Расчет. Приводим сечение складчатого элемента к двутавровому (рис. 33). Толщина стенки элемента двутаврового сечения
tω = (22×4)/sinβ = 88/0,94 = 94 мм.
Рис. 33. Сечения армоцементного складчатого покрытия
а - поперечное; б - расчетное; в - приведенное к стальному
Вычисляем коэффициент армирования двумя сетками № 10-1 по табл. 1 прил. 1, коэффициент армирования при одной сетке на 1 см равен 0,0071, толщина стенки 2,2 см.
μm1 = (0,0071×2)/2,2 = 0,0065.
Коэффициент армирования стержнями Æ = 5 мм.
μs = (50,3×8)/(800×22) = 0,022.
Коэффициенты приведенного армирования равны:
а) для сжатой полки из выражения (4)
μ'm1 = μ'm + μ'sRsc/Rmc = 0,0065 + 0,025 = 0,0315.
Для определения расчетного эксцентриситета ec продольной силы определяем коэффициент увеличения эксцентриситета η по зависимости (29):
η = 1/(1 - N/Ncrt).
Вычисляем величины Ncrt по СНиП 2.03.01-84 для сечений с ненапряженной арматурой
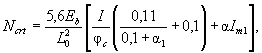
где I - момент инерции бетонного сечения вычисляем из выражения
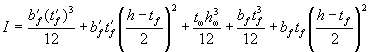 = 800×223
: 12 + 800×22(1000 - 22 : 2)2 + 94×9563
: 12 + 800×223 : 12 + 800×22(1000
- 22) : 2 = 11512,455×106 мм4.
= 800×223
: 12 + 800×22(1000 - 22 : 2)2 + 94×9563
: 12 + 800×223 : 12 + 800×22(1000
- 22) : 2 = 11512,455×106 мм4.
Момент инерции сетчатой арматуры Im1 = I1 - I = 413,35×106 мм4.
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, определяется из выражения (21) СНиП 2.03.01-84, принимая коэффициент β = 1,3 как для мелкозернистого бетона группы А.
φe = 1 + βM1I/M1 = 1 + 1,3×146 : 274 = 1,6;
α = Em1/Eb;
по формуле (87) Em1 = (Emμm + Esμs)/(μm + μs) = (150000×0,0065 + 170000×0,022) : (0,0065 + 0,022) = 165438,6 МПа, тогда α = 165438,6 : 27500 = 6,01.
Коэффициент α1 принимается равным ec/h, но не менее величины α1min = 0,5 - 0,01l0/h - 0,01Rb; ec = M/N = 274/555 = 0,494 м.
Определяем расчетную длину арки:
l0 = 0,54; la = 19440×0,54 = 10490 мм;
α1min = 0,5 - 0,01×10490/1000 - 0,01×18 = 0,216;
коэффициент α1 = ec/h = 0,494/1,000 = 0,494 > 0,216.
Ncrt = 5,6Eb{I[0,11/(0,1 + α1) + 0,1]/φc + αIm1)/l20 = 5,6×27500{11512,455×106[0,11 : (0,1 + 0,494) + 0,1] : 1,6 + 6,01×413,348×106} : 104902 = 6687367 Н = 6687,37 кН.
Полученную величину подставляем в выражение (29)
η = 1/(1 - N/Ncrt) = 1 : (1 - 555 : 6687) = 1,09.
Расчетный эксцентриситет ec продольной силы с учетом коэффициента η равен:
ec = Mη/N = 274×1,09 : 555 = 0,538 м.
Эксцентриситеты силы Ne1 и e2 равны:
e' = ec - h/2 + t'f/2 = 538 - 500 + 22 : 2 = 49 мм.
Для определения, какой случай внецентренного сжатия имеет место в рассматриваемом сечении, находим высоту сжатой зоны x по формуле (41).
Когда сечение симметричное, ycm = h - t/2 = 489 мм, тогда et = ec + ycm = 538 + 489 = 1027 мм;
e' = ec - h + t'f/2 = 1027 - 1000 + 22 : 2 = 38 мм.
Для вычисления высоты сжатой зоны в сечении сначала вычисляем значения γ1, γ2 и γ3:
из выражения (42)
γ1 = (1027 - 1000)(800×22 - 94×22) - 94×222/2 + 800×222/2 = 590216;
из выражения (43)
γ2 = 0,0065×590218 + 800×22(0,0315 - 0,0065)38 = 20556,6;
из выражения (44)
γ3 = 94×0,0065(1000×1027 - 10002/2 - 22×1027 + 222/2) + 800×22×0,0315(1027 - 22/2) = 871540.
Полученные значения коэффициентов подставляем в выражение для определения высоты сжатой зоны.
Высота сжатой зоны
x = -(1027 - 1000) ± ![]() =
-27 ±
=
-27 ± ![]() = -27 ± 446,5 = 420
мм.
= -27 ± 446,5 = 420
мм.
В соответствии с выражением (8) граничное значение относительной высоты сжатой зоны бетона
ξR = ω/[1 + σs(1 - ω/1,1)/500] = 0,34 : [1 + 360(1 - 0,34 : 1,1) : 500] = 0,23,
где ω = 0,5 - 0,008Rb = 0,34.
Значит: ξ = x/h = 0,42 > ξR = 0,23; x = 420 мм > t'f = 22 мм.
Прочность сечения определяем по формуле (34)
N ≤ Nc - (Nc - Nin)[2ec/ein - (ec/ein)2].
Для вычисления несущей способности центрально сжатого элемента Nc находим следующие величины:
Rc1 = Rb + R'mcμ'm1 = 19,5 + 245×0,0315 = 27,22 МПа;
Rω1 = Rb + R'mcμ'mω1 = 19,5 + 245×0,065 = 19,59 МПа;
Rf1 = Rb + R'mcμ'mf1 = 19,5 + 245×0,0315 = 27,22 МПа;
Afc = 800×22 = 17600 мм2;
Aω = 94(1000 - 2×22) = 89864 мм2;
Aft = 800×22 = 17600 мм2.
Несущая способность центрально сжатого сечения по формуле (40)
Nc = 27,22×17600 + 19,59×89864 + 27,22×17600 = 2718 кН.
Несущая способность для сечения, в котором высота сжатой зоны x = ξRh, определяется из условия (42) при x > t'f:
Nin = Rc1Abfc + Rω1Abωc - Rmμmω1Abωt - Rmμmf1Aft.
где x = ξRh = 0,23×1000 = 230 мм;
Aωc = (x - t'f)tω = (230 - 22)94 = 19552 мм2;
Abωt = tω(h - x - t'f) = 94(1000 - 230 - 22) = 70312 мм2;
Aft = 22×80 = 17600 мм2.
После подстановки вычисленных величин в формулу (42) получим
Nin = 27,22×17600 + 19,59×19552 - 245×0,0065×70312 - 245×0,0315×17600 = 614295 Н = 614,3 кН.
Эксцентриситет продольной силы, определяемой по формуле (44),
ein = (S*c + S*ωc + S*ωt + S*t)/Nin,
S*ωc = Rω1Aωc[h - yc - t'f - (x - t'f)/2) = 19,59×19552[1000 - 500 - 22 - (230 - 22) : 2] = 141,7×106 мм3;
S*ωt = 245×0,0065×94(956 - 230 + 22)[500 - (956 - 230 + 22)/2 - 22] = 11,6×106 мм3.
S*c = Rc1bft'f(h - yc - tf/2) = 234,2×106 мм3;
S*t = Rm1μmt1bftf(yc - tf/2) = 66,4×106 мм3.
Полученные величины подставим в формулу (44)
ein = (S*c + S*ωc + S*ωt + S*t)/Nin = (234,2×106 + 141,7×106 - 11,6×106 - 66,4×106) : 614295 = 485,2 мм.
Несущая способность внецентренно сжатого сечения после подстановки в формулу (34)
N ≤ Nc - (Nc - Nin)[2ec/ein - (ec/ein)2] = 2718000 - (2718000 - 614295)[2×538 : 485,2 - (538 : 485,2)2] = 636435 Н = 636,4 кН.
Прочность складчатого покрытия обеспечена, так как N = 636,4 кН > N = 555 кН.
Пример 10.
Дано. Двухскатное покрытие здания из сборных длинномерных армоцементных складчатых панелей. Требуется проверить на прочность нормального сечения в середине пролета. Приведенное сечение панели двутавровое: высота сечения h = 1000 мм, ширина полки b'f = 400 мм, t'f = 30 мм, толщина наклонной стенки tω = 20 мм (рис. 34).
Рис. 34. Армоцементный складчатый внецентренно сжатый элемент покрытия
а - продольное сечение; б - поперечное сечение; в - сечение, приведенное к стальному
Расчетный пролет l = 14,9 м. Из статического расчета покрытия были определены усилия, действующие в сечении:
от расчетных нагрузок M = 69,2 кН×м; N = 50 кН.
Складчатая панель армируется восемью сварными сетками № 12,5; Æ = 0,5 мм; ТУ 14-4-713-76 в сжатой и растянутой полках сечения (коэффициент сетчатого армирования μ при одной сетке на 1 см толщины сечения элемента μm = 0,0014), четырьмя сварными сетками № 12,5; Æ = 0,5 мм; ТУ 14-4-713-76 в наклонных гранях сечения;
сварными плоскими каркасами из арматуры диаметром 10 мм класса А (в сжатой и растянутой полках). Сечение обычной арматуры A's = As = 78,5×2 = 157 мм2. Расчетное сопротивление и модуль Es упругости сварных сеток принимаем по табл. 11 и п. 2.25: Rm = Rmc = 245 МПа; Em = 150000 МПа.
Расчетное сопротивление для арматуры класса А-III принимаем по СНиП 2.03.01-84: Rs = Rsc = 365 МПа, Es = 200000 МПа.
Для мелкозернистого бетона класса В20 сжатие осевое принимаем: по табл. 7 (призменная прочность) Rb = 10,5 МПа; по табл. 10 Eb = 22000 МПа.
Проверим прочность нормального сечения.
Расчет. Толщина вертикальной стенки таврового сечения определяется из выражения tω = 2×20/sinα = 2×20/0,865 = 46 мм.
Влияние прогиба на величину эксцентриситета продольного усилия учитываем путем расчета конструкции по деформированной схеме, принимая во внимание неупругие деформации материала и наличие трещин по п. 3.16.
Влияние прогиба элемента учитываем путем умножения эксцентриситета ec на коэффициент η, определяемый по формуле (29)
η = 1/(1 - N/Ncrt).
Момент инерции бетонного сечения
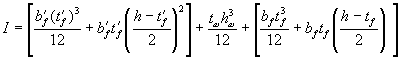 = [40×33
: 12 + 40×3(100 - 3) : 22] + 4,6×933
: 12 + [40×3(100 - 3) : 2] = 883110 см4.
= [40×33
: 12 + 40×3(100 - 3) : 22] + 4,6×933
: 12 + [40×3(100 - 3) : 2] = 883110 см4.
Момент инерции приведенного сечения арматуры
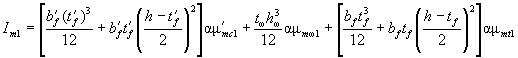
![]() =
[40×33
: 12 + 40×3(100 - 3)2 : 22]5,26×0,0446
+ 4,6×943
: 12×5,26×0,0062
+ [4×33
: 12 + 40×3(100 - 3)2 : 22]5,25×0,0466
= 142612 см4.
=
[40×33
: 12 + 40×3(100 - 3)2 : 22]5,26×0,0446
+ 4,6×943
: 12×5,26×0,0062
+ [4×33
: 12 + 40×3(100 - 3)2 : 22]5,25×0,0466
= 142612 см4.
Определяем расчетную длину элемента l0 = 0,58×14900 = 8642 мм.
Критическая условная сила сжатия (см. пример 9)
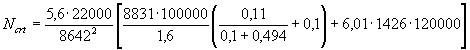 =
4000 кН.
=
4000 кН.
Коэффициент увеличения эксцентриситета по формуле (29)
η = 1/(1 - 5/4000) = 1.
Эксцентриситет продольной силы вычисляем по формуле
ec = M/N = 69×200000/50000 = 1384 мм.
Эксцентриситет продольной силы
e'c = ecη = 1384×1 = 1384 мм.
Определяем коэффициент:
армирования сварными сетками сжатой и растянутой полок
μ'mc = μmt = μωh/t'f = 0,0014×8 : 2 = 0,0037,
вертикальной стенки
μmω = μωh/tω = 0,0014×4 : 2 = 0,0028.
Эксцентриситет продольной силы относительно центра тяжести сжатой полки
e'c = e'c - (h - t'f)/2 = 1384 - (1000 - 30) : 2 = 899 мм.
Коэффициент армирования сжатой и растянутой полок стержневой арматурой
μs = μ's = As/Ab = 157 : (400×30) = 0,013.
Коэффициент приведенного армирования сжатой и растянутой полок определяем по формуле (10)
μ'm1 = μmf1 = μ'mc + μsRb/Rm = 0,0037 + 0,013×365 : 245 = 0,023.
Предельная высота сжатой зоны по формуле (8) ξR = 0,275. Определяем высоту сжатой зоны по зависимости (34). Величины для подстановки в зависимость (34) вычисляем следующим образом:
et = e'c + ycm = 1384 + 500 = 1884 мм;
e2 = e'c + ycm - h = 1884 + 500 - 1000 = 1384 мм;
γ1 = (et - h)(b'ft'f - tωt'f) - tω(t'f)2/2 + b'f(t'f)2/2 = (1884 - 1000)(400×30 - 46×30) - 46×302 : 2 + 400×302 : 2 = 9547380;
γ2 = μmωγ1 + b'ft'f(μmc1 - μmω)e2 = 0,0028×9547380 + 400×30(0,023 - 0,0028)884 = 241013,7;
γ3 = tωμmω(het - h2/2 - tfet + t2f/2) + bftfμm1(et - tf/2) = 46×0,0028(1000×1884 - 10002 : 2 - 30×1884 + 302 : 2) + 400×30×0,023(1884 - 30 : 2) = 686862.
Высота сжатой зоны
x
= -(et - h) ± ![]() =
-(1884 - 1000) ±
=
-(1884 - 1000) ± ![]() = -884
+ 902 = 18 мм.
= -884
+ 902 = 18 мм.
Отношение x/h = 18/1000 = 0,018 < ξR = 0,275.
В соответствии с требованиями п. 3.18 при ξ = x/h = 0,018 < ξR = 0,275 и так как x < t'f, прочность внецентренно сжатого двутаврового элемента определяем из формулы (38)
Ne'c ≤ Rmμmω1Aω(hω + tf)/2 + Rmμmf1Aft[h - (tf + t'f)/2] = 245×0,0028×44160(940 + 30) : 2 + 245×0,023×12000[1000 - (30 + 30) : 2] = 80283842 Н×мм.
Нормальная сила N = 80283842/1384 = 58008 Н = 58 кН. Площади поперечных сечений, необходимые для расчета по формуле (38), равны:
Aω = tωhω = 46×960 = 44160 мм2;
Aft = bftf = 400×30 = 12000 мм2.
Прочность приведенного двутаврового сечения N = 58 кН > 50 кН.
Пример 11.
Дано. Элемент кольцевого сечения с наружным радиусом re = 500 мм, внутренним радиусом rin = 470 мм. Бетон класса В35 с прочностью на осевое сжатие Rb = 19,5 МПа. Армирование стенки элемента кольцевого сечения выполнено из двух тканых сеток № 10-1 и сварной сетки из проволоки 4 мм класса Вр-I, шаг 150 ´ 150 мм, нормативное сопротивление арматуры Rs, ser = 500 МПа. Расчетное сопротивление Rs = 450 МПа.
В сечении действуют изгибающий момент M = 14 кН×м и нормальная сила N = 19 кН.
Требуется рассчитать прочность сечения.
Расчет. Определяем коэффициент армирования стенки кольцевого сечения:
Am = πdm/4 = 3,14×22/4 = 314 мм2; μm = Am/t×20 = 314/300 = 0,0105.
Прочность внецентренно сжатого кольцевого сечения определяем по зависимости (50) при rm = (ri + re)/2 = (250 + 235)/2 = 242,5.
Величину относительной площади сжатой зоны бетона определяем по формуле (51) при Abr = 2πrmtr = 2×3,14×242,5×15 = 22843,5 мм2
![]()
В соответствии с п. 3.20 полученное значение αr = 0,93 > 0,15; в формулу (50) подставляем значение αr, вычисленное по формуле (52),
αr = (N + 0,73Rmμmr1Abr)/[(Rb + 2Rmμmr1)Abr] = (80 + 0,73×450×0,0105×22843,5)/[(35 + 2×450×0,0105)22843,5] = 0,106.
Расчетное сопротивление
Rr1 = Rb + Rmμmr1 = 19,5 + 450×0,0105 = 24,225 МПа.
После подстановки полученных значений в формулу (50) получим
Nec ≤ 22843,5[24,285sin(180)×0,106/3,14 + 450×0,0105(1 - 1,35×0,106)1,6×0,106]242,5 = 14685343 Н×мм.
Эксцентриситет продольной силы ec = M/N = 58600000/80000 = 736,8 мм. Прочность сечения N = 14685343/736,8 = 19931 Н = 19,93 кН > 19 кН, что удовлетворяет заданному усилию.
Пример 12.
Дано. Стенка армоцементной цилиндрической емкости для хранения сыпучих материалов. Толщина стенки t = 25 мм. Бетон класса В35, группа А с прочностью на осевое сжатие (Rb = 19,5 МПа). Стенка армируется шестью слоями тканых сеток № 10-1 по ГОСТ 3826-82* с расчетным сопротивлением Rm = Rmc = 245 МПа и одним слоем сварной сетки из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I, Æ = 5 мм, шаг 100 ´ 100 мм. Расчетное сопротивление арматуры для предельных состояний первой группы Rs = Rsc = 360 МПа. Осевое усилие растяжения стенки (нормативное) N = 155 кН. Расчетное растягивающее усилие Nc = 166 кН.
Требуется рассчитать сечение стенки по прочности от действия осевого усилия растяжения.
Расчет:
а) коэффициенты армирования при коэффициенте армирования одной сеткой на 1 см μm = 0,0071.
μmt = 6μ/t = 6×0,0071/2,5 = 0,017;
б) сварными сетками из стальной низкоуглеродистой холоднотянутой проволоки (на участке стенки высотой t = 1 м), шаг сетки 100 мм, диаметр стержней равен 5 мм.
μs = As/Ab = 10×19,63/25×1000 = 0,00785.
Коэффициент приведенного армирования
μm1 = μmt + μsRs/Rm = 0,017 + 0,00785×360 : 245 = 0,0285.
Прочность центрально растянутой стенки определяется в соответствии с требованиями п. 3.32 по формуле (53)
N ≤ Rmμm1bt = 245×0,02285×1000×25 = 174,79 кН;
N = 174,8 > Nc = 166 кН,
т.е. прочность сечения обеспечена.
Пример 13.
Дано. Элемент внецентренно растянутый толщиной t = 25 мм и шириной 1000 мм. Бетон мелкозернистый класса В30 группы В. Прочность бетона на осевое сжатие Rb = 170 МПа. Элемент армируется только шестью слоями тканой сетки № 10-1, ГОСТ 3826-82*, Rm = Rmc = 245 МПа. Сварная сетка из стальной проволоки класса Вр-I, Æ = 5 мм. Осевое усилие растяжения N = 6,5 кН. Изгибающий момент M = 0,12 кН×м. Требуется рассчитать внецентренно растянутое сечение армоцементного элемента по прочности.
Расчет. Коэффициент сетчатого армирования при μm = 0,0071 равен:
μm1 = 6μm/t = 6×0,0071/2,5 = 0,017.
Определяем эксцентриситет нормальной силы
ec = M/N = 0,12/6,5 = 0,018 > h/2.
Прочность внецентренно растянутого элемента для случая приложения силы N за пределами сечения определяем по (55)
Ne = Rmμm1b[(h - x)/2]2 - (Rb + Rmsμm1)bx2/2.
Высота сжатой зоны определяется из зависимости (56). Для вычисления высоты сжатой зоны определяем коэффициенты γ1 = 0 и γ2 = 0. Значение γ3 находим из выражения (49)
γ3 = bμm1(he1 + h2/2) = 1000×0,0285(25×30,5 + 252 : 2) = 30637,5.
Эксцентриситет продольной силы относительно грани растянутой зоны
et = ec + h/2 = 18 + 25 : 2 = 30,5 мм.
Высота сжатой зоны
x
= -(et - h) ± ![]() =
-(30,5 - 25) ±
=
-(30,5 - 25) ± ![]() = 16,5 мм,
= 16,5 мм,
и отношение ξ = x/h = 0,66. Предельное отношение определяем по формуле
ξR = ω/[1 + σm(1 - ω/1,1)400] = 0,364 : [1 + 245(1 - 0,364 : 1,1) : 400] = 0,26,
где ω = 0,5 - 0,008×17 = 0,364.
Так как x/h = 0,66 > ξR = 0,26, то в условие прочности (55) подставляем значение x = ξRh = 0,26×25 = 6,45 мм. После подстановки получаем
Ne ≤ Rmμm1b[(h - x)/2]2 - (Rb + Rmμm1)bx2/2 = 245×0,0285×1000[(25 - 6,45) : 2]2 - (18 + 245×0,0285)1000×6,452 : 2 = 81089 Н×мм.
Несущая способность N = 81089/18 = 4,5 кН. Прочность элемента не обеспечена.
Дано. Армоцементный внецентренно растянутый элемент толщиной t = 25 мм и шириной 1000 мм выполнен из мелкозернистого бетона класса В35, группы А, прочностью на осевое сжатие Rb = 18 МПа.
Элемент армируется шестью слоями тканой сетки № 10-1 ГОСТ 3826-82*, расчетное сопротивление Rm = Rmc = 245 МПа и сварной сеткой из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I, Æ = 5 мм, шаг 100 мм. Нормативное сопротивление растяжению Rsn = Rs, ser = 395 МПа. Расчетное сопротивление арматуры для предельных состояний первой группы Rsc = 360 МПа. Армоцементный элемент работает на осевое растяжение с усилием N = 139 кН и изгибается моментом M = 0,5 кН×м.
Требуется рассчитать сечение внецентренно растянутого элемента по прочности.
Расчет. Коэффициент сетчатого армирования в соответствии с требованиями п. 3.3 при коэффициенте армирования одной сеткой на 1 см толщины элемента μm = 0,0071 равен:
μmt = 6μm/t = 6×0,0071/2,5 = 0,017.
Коэффициент армирования сварными сетками из стальной низкоуглеродистой холоднотянутой проволоки (на участке шириной t = 1 м, шаг сетки 100 мм, Æ = 5 мм)
μs = As/Ab = 10×19,63/25×1000 = 0,00785.
Коэффициент приведенного армирования
μmt1 = μmt + μsRs/Rm = 0,017 + 0,00785×360 : 345 = 0,0285.
Расчет внецентренно растянутых элементов прямоугольного сечения с арматурой, приведенной к равномерно распределенной, производится в соответствии с п. 3.23.
Эксцентриситет нормальной силы ec = M/N = 0,5/140 = 0,0036 м. Находим расстояние от центра массы сечения элемента до ядровой точки. Площадь сечения A = 25×1000 = 25000 мм.
Момент сопротивления
W = I/ycm = bt3/12(t/2) = 1000×253 : 12 : (25 : 2) = 104166,7 мм3.
Радиус инерции r = W/A = 104166,7/25000 = 4,17 мм.
Поскольку продольная сила приложена в пределах ядра сечения, так как ec = 3,6 мм < r = W/A = 4,17 мм, то расчет прочности производим по формуле (54) с коэффициентом γ = 0,8.
N ≤ γRmμmt1bh = 0,8×245×0,0285×1000×25 = 139,65 кН.
Поскольку N = 139,65 кН > N' = 139 кН, то прочность элемента обеспечена.
Пример 15.
Дано. Сечение то же, что и в примере 14.
Осевое усилие растяжения элемента N = 100 кН. Изгибающий момент M = 0,7 кН×м.
Требуется рассчитать внецентренно растянутый элемент по прочности.
Расчет. Коэффициенты сетчатого армирования те же, что и в прим. 14.
В соответствии с п. 3.22б, если продольная сила N приложена между ядром сечения и наружной гранью сечения, прочность внецентренно растянутого сечения определяется из условия (54), в котором коэффициент γ принимается равным 0,6.
Эксцентриситет продольной силы ec = M/N = 0,7/60 = 0,012 м. Так как ec = 12 мм > r = W/A = 4,17 мм, продольная сила, приложенная между ядром сечения и наружной гранью, и прочность сечения равна:
N = γRmμmt1bh = 0,6×245×0,0285×1000×25 = 104,7 кН.
Так как N = 104,7 кН > N = 100 кН, прочность элемента обеспечена.
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.23 (3.20). Расчет по прочности наклонных сечений должен производиться:
по сжатому бетону между наклонными трещинами;
по наклонной трещине на действие поперечной силы;
по наклонной трещине на действие изгибающего момента.
3.24. Для армоцементных элементов прямоугольного сечения должно соблюдаться условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами:
Q ≤ 0,3φω1φb1Rbbωhω. (57)
Рис. 35. Сечение и схема усилий в элементе при расчете его по прочности сечений, наклонных к продольной оси элемента
Коэффициент φω1, учитывающий влияние поперечных и продольных проволок сеток, определяется по формуле
φω1 = 1 + 5Emμmω1/Eb. (58)
Коэффициент φb1 определяется по формуле
φb1 = 1 - 0,01Rb, (59)
где значение Rb принимается в МПа.
3.25. Расчет прочности сечений, наклонных к продольной оси армоцементного элемента, на поперечную силу (рис. 35) должен производиться из условия
Q ≤ Qm + Qb, (60)
где Q - поперечная сила, определяется внешней нагрузкой, расположенной по одну сторону от рассматриваемого наклонного сечения; Qm - поперечная сила, воспринимаемая поперечными проволоками сетки, пересекающими наклонную трещину; Qb - поперечная сила, воспринимаемая бетоном сжатой зоны в наклонном сечении.
Значение Qm определяется по формуле
Qm = qmωaq, (61)
где aq - проекция наклонной трещины; угол наклона трещины принимается равным 45°; qmω - интенсивность армирования элемента поперечными проволоками сеток в пределах наклонной трещины, определяемая по формуле
qmω = Rmωμmω1tω/sin(90° - β); (62)
здесь μmω1 - коэффициент приведенного армирования стенки при расчете на поперечную силу, определяемый по формуле
μmω1 = Amω/(tωhω) + AsωRsω/(tωRmω), (63)
Amω - площадь сечения поперечных проволок сеток, расположенных в пределах наклонной трещины; Asω - площадь сечения поперечных стержней, пересекающихся в пределах наклонных трещин; tω - толщина стенки, воспринимающей поперечную силу; β - угол наклона стенки складчатого элемента к вертикальной оси сечения.
Значение поперечной силы Qb для изгибаемых и внецентренно сжатых элементов определяется по формуле
Qb = 0,75Rbttωh2ω/[aqsin(90° - β)], (64)
где tω и h - соответственно ширина и высота элемента в рассматриваемом сечении.
Примечание. Rbt - принимается с коэффициентом γb п. 2.11, который определяется по отношению главных сжимающих и главных растягивающих напряжений в наклонном сечении.
В случае когда граница сжатой зоны располагается в пределах полки, допускается принимать aq = hω.
3.27 (3.23). Расчет сечений, наклонных к продольной оси элемента, на действие изгибающего момента должен производиться из условия
M ≤ (RsAs + Rmμmf1b'ft'f)[h - (t'f + tf)/2] + 1,41Rmμmω1tωhω(hω + t'f)/2, (65)
где M - момент всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения относительно оси, проходящей через точку приложения равнодействующей усилий в сжатой зоне и перпендикулярной плоскости действия момента.
Высота сжатой зоны в наклонном сечении, измеренная по нормали к продольной оси элемента, определяется из условия равновесия проекций усилий в бетоне и арматуре наклонного сечения на продольную ось элемента.
Проверка на действие изгибающего момента не производится для наклонных сечений, пересекающих растянутую грань элемента на участках, обеспеченных от образования нормальных к оси элемента трещин, т.е. там, где момент M от внешней нагрузки, на которую ведется расчет по прочности, меньше или равен моменту трещинообразования Mcrc, определяемому по формуле (125) СНиП 2.03.01-84, в котором значение Rbt, ser заменяется Rbt.
ПРИМЕРЫ РАСЧЕТА
Пример 16.
Дано. Складчатая панель покрытия в соответствии с данными, приведенными в прим. 2 (рис. 26).
Требуется рассчитать складчатую панель по прочности наклонного сечения. В соответствии с п. 3.24 должно соблюдаться условие по формуле (57), обеспечивающее прочность по сжатому бетону между наклонными трещинами, где коэффициент, учитывающий влияние поперечных проволок сеток, равен:
φω1 = 1 + 5Emμmω1/Eb = 1 + 5×150000×0,00465 : 28500 = 1,12.
Коэффициент, учитывающий бетон, φb1 = 1 - 0,01; Rb = 1 - 0,01×22 = 0,78.
Из условия (57) определяем Q ≤ 3,4φω1φb1Rbbhω = 0,3×1,12×0,78×22,66×240 = 91329,6 Н.
Максимальная поперечная сила от внешней нагрузки равна 526 Н. Условие (57): Q = 8526 Н < Q = 91329,6 Н выполнено. Прочность сжатого бетона между наклонными трещинами обеспечена. Расчет на поперечную силу выполняем по условию (60). Так как граница сжатой зоны располагается в пределах полки, принимаем aq = hω = 240 мм. Интенсивность армирования [по формуле (62)] элемента поперечными стержнями сеток qmω = 206×0,00465×5,6/0,5 = 107,3 МПа.
Поперечная сила, воспринимаемая поперечными проволоками по формуле (61), равна Qm = 107,3×240 = 25752 Н. Поперечная сила, воспринимаемая бетоном сжатой зоны по формуле (64),
Qb = 0,75Rbttωh2/aq = 0,75×1,36×5,6×2802 : 240 = 18659,2 Н.
Прочность по наклонному сечению равна: Q = (186,59 + 257,52)102 = 444110 Н > Q = 8526 Н, т.е. прочность по наклонному сечению обеспечена.
Расчет по наклонному сечению преднапряженного элемента на действие изгибающего момента производится по формуле (65). Размеры сечения Rsp, Asp, Rm1, μmf1, μmω1 (см. прим. 2)
M ≤ (RspAsp + Rmμmf1b'ft'f)[h - (t'f + tf)/2] + 1,41Rmμmω1tωhω(hω + t'f)/2 = (1240×28,28 + 245×0,0117×250×20)[280 - (20 + 20) : 2] + 1,41×245×0,00465×240×56(240 + 20) : 2 = 24,768 Н×мм = 24,8 кН×м.
Прочность сечения обеспечена.
Пример 17.
Дано. Элемент с приведенным двутавровым сечением с размерами: высота сечения h = 240 мм, ширина полки b'f = 920 мм, толщина полки t'f = 20 мм, толщина вертикальной стенки tω = 165,5 мм, ширина нижней растянутой полки bf = 1840 мм, толщина растянутой полки tf = 25 мм. Бетон мелкозернистый класса В35, группы Б с прочностью на осевое сжатие Rb = 19,5 МПа и прочностью на осевое растяжение Rbt = 1,15 МПа. Начальный модуль упругого бетона Eb = 28500 МПа. Поперечная сила Q = 68 кН. Армирование предусмотрено двумя ткаными сетками № 10-1 по ГОСТ 3826-82* по всему сечению (соответствующий коэффициент сетчатого армирования μm = 0,0071).
Верхняя и нижняя полки дополнительно армируются сварным сетками из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I в сжатой зоне - восемь стержней диаметром 3 мм, A's = 8×7,1 = 56 рассчитывается по приведенному сечению с толщиной стенки tω = 165,5 мм по условию (57).
Коэффициент, учитывающий влияние поперечных ,8 = 57 мм2; в растянутой зоне - 28 стержней диаметром 4 мм, Ay = 28×12,6 = 352,8 мм2.
Требуется рассчитать двутавровое сечение по прочности наклонного сечения.
В соответствии с п. 3.24 проверяем, обеспечивается ли условие прочности по бетону между наклонными трещинами. Складчатая панель и продольных проволок сетки φω1, определяемый по формуле (58), равен:
φω1 = 1 + 5Emμmω1/Eb = 1 + 5×150000×0,0071 : 27500 = 1,19.
Коэффициент φb1, определяемый по формуле (59), равен:
φb1 = 1 - 0,01Rb = 1 - 0,01×19,5 = 0,8;
Q ≤ 0,3φω1φb1Rbbωhω = 0,3×1,19×0,8×19,5×165,5×195 = 179 кН.
Прочность по сжатому бетону между трещинами обеспечена, так как Q = 179 кН > Q = 75 кН.
Интенсивность армирования элемента поперечными проволоками сеток в пределах наклонной трещины, определяемая по формуле (62), равна:
qmω = Rmωμmω1tω/sinβ.
Коэффициент приведенного армирования стенки при расчете на поперечную силу, определяемый по формуле (78)
μmω1 = Amω/tω1 = 0,0071, тогда qmω = 206×0,0071×165,5/0,865 = 279,84 Н×мм.
Поперечная сила, воспринимаемая поперечными проволоками, вычисленная по формуле (61), равна:
Qm = qmωaq = 279,84×195 = 54568,5 Н = 54,57 кН.
Поперечная сила, воспринимаемая бетоном сжатой зоны, вычисленная по формуле (64), равна:
Qb = 0,75Rbttωh2ω/aq = 0,75×1,15×165,5×1952 : 195 = 13,9 кН.
Прочность сечения по наклонному сечению Q = Qm + Qb = 54,57 + 13,9 = 68,5 кН. Так как Q = 68,5 кН > Q = 68 кН. Прочность элемента по наклонному сечению обеспечена.
Пример 18.
Дано. Армоцементный элемент пролетом 5,9 м имеет прямоугольное сечение hω = 200 мм, tω = 40 мм (рис. 26). Изгибающий момент, действующий в сечении у опоры равен M = 5,5 кН×м; поперечная сила в сечении Q = 20 кН. Бетон для бетонирования элемента принят мелкозернистый класса В40, группы А. Сечение армируется шестью сварными сетками для армоцемента (Æ = 0,5 мм, ТУ 14-4-713-76) прил. 1 и арматурой из высокопрочной гладкой проволоки Вр-II Æ = 3 мм. Требуется произвести расчет по прочности наклонного сечения. Расчетные характеристики сварной сетки для армоцемента: Rm = 245 МПа, Rmω = 206 МПа, Em = 150000 МПа. Расчетные сопротивления мелкозернистого бетона: Rb = 22 МПа, Rbt = 1,4 МПа, Eb = 28,5×103 МПа. Расчетные сопротивления высокопрочной гладкой проволоки класса В-II Rs = 1240 МПа, Esp = 200000 МПа.
Проверяем условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами по формуле (57).
Коэффициент, учитывающий влияние поперечных проволок сеток, равен при μmω1 = 0,0031×6/4 = 0,00465; φω1 = 1 + 5×150000/28500×0,00465 = 1,12; φb1 = 1 - 0,01×22 = 0,78. Тогда по формуле (57)
Q = 0,3×1,12×0,78×22×40×200 = 46126 Н.
Максимальная поперечная сила от внешней нагрузки Q = 40000 Н, значит условие (57) выполнено, прочность бетона между наклонными трещинами обеспечена.
Расчет по прочности наклонного сечения выполняем по условию (60).
Интенсивность поперечного армирования по формуле (62)
qmω = 206×0,00465×40/0,5 = 76,6 МПа.
Поперечная сила, воспринимаемая поперечными проволоками сетки по формуле (61), равна Qm = 76,6×200 = 15320 Н.
Поперечная сила, воспринимаемая бетоном сжатой зоны по формуле (64), равна:
Qb = 0,75Rbttωh2ω/[aqsin(90° - β)] = 0,75×1,4×40×2002 : (200×0,96) = 80,64 Н.
Прочность наклонного сечения по формуле (60) равна:
Q = 8064 + 15320 = 23384 Н > Q = 20000 Н.
Прочность наклонного сечения на действие поперечной силы обеспечена.
Расчет наклонного сечения на действие изгибающего момента производим по формуле (65). Для прямоугольных сечений прочность
M ≤ RsAsh + 1,41Rmμmω1tωh2ω/2 = 1240×21,21×200 + 1,41×245×0,0046×40×200 : 2 = 6545154 Н×мм.
Поскольку M = 6,54 кН×м > M = 5,5 кН×м, прочность наклонного сечения на действие изгибающего момента обеспечена.
Пример 19.
Дано. Двухскатное покрытие здания из сборных длинномерных складчатых панелей сечением пятигранной складки: b'f = 400 мм, t'f = 30 мм; h = 1000 мм, hω = 940 мм, bf = 400 мм, tf = 30 мм; толщина стенки приведенная tω = 46 мм. Угол наклона стенок α = °60. Сечение армируется в пределах верхней сжатой и нижней растянутой полок восемью слоями сетки № 12-05 по ТУ 14-4-713-76, а в пределах наклонных граней сечение - четырьмя сварными сетками № 12-05 по ТУ 14-4-713-76. В пределах сжатой и растянутой полок сечение армируется дополнительно сварными каркасами из арматуры класса А-III, Æ = 10 мм.
A' = As = 78,5×4 = 314 мм2.
Расчетное сопротивление и модули упругости арматуры и бетона: сварных сеток Rm = 245 МПа, Rmω = 206 МПа, Em = 150000 МПа; сварных каркасов Rs = 365 МПа, Es = 200000 МПа. Бетон мелкозернистый класса В30 - Rb = 15,5 МПа и Rbt = 1,1 МПа, Eb = 26000 МПа.
В сечении действует поперечная сила Q = 30 кН, M = 130 кН×м. Требуется рассчитать прочность сечения на поперечную силу.
Расчет. Коэффициенты сетчатого армирования стенки (при одной сетке на 1 см толщины стенки μm = 0,0014) равны:
μmω1 = μmn/tω = 0,0014×4 : 4,6 = 0,0012;
μmf = 0,0014×8/3 = 0,0037.
Коэффициент, учитывающий влияние поперечных и продольных проволок сеток
φω1 = 1 + 5Emμmω1/Eb = 1 + 5×150000×0,0012 : 26000 = 1,04.
Коэффициент φb1 определяем по формуле (59)
φb1 = 1 - 0,01Rb = 1 - 0,01×15,5 = 0,845.
Проверяем условие, обеспечивающее прочность по сжатому бетону, по формуле (57)
Q ≤ 0,3×1,04×0,845×15,5×46,94 = 176697 Н.
Поскольку Q = 30 кН < Q = 177 кН, условие (57) выполнено, прочность на сжатие между наклонными трещинами обеспечена.
Расчет по прочности сечения, наклонного к продольной оси армоцементного сечения на поперечную силу, производится из условия (60).
Интенсивность армирования элемента поперечными проволоками, по формуле (62), равна:
qmω = Rmωμmω1tω/sinβ = 206×0,0014×46 : sin60° = 15,32 МПа.
Поперечная сила, воспринимаемая поперечными проволоками, по формуле (67), равна:
Qm = qmωaq = 15,32×940 = 14400 Н = 14,4 кН.
Поперечная сила, воспринимаемая бетоном сжатой зоны, по формуле (64), равна:
Qb = 0,75Rbttωh2ω/[aqsin(90° - β)] = 0,75×1,1×46×9402 : 940 = 17,8 кН.
Прочность элемента по наклонному сечению по формуле (60) равна:
Q = Qm + Qb = 14,4 + 17,8 = 32,2 кН.
Поскольку Q = 32,2 кН > Q = 30 кН, прочность элемента обеспечена.
Прочность сечения, наклонного к продольной оси элемента, на действие изгибающего момента по формуле (65) равна:
M = (RsAs + Rmμmf1b'ft'f)[h - (t'f + tf)/2] + 1,41Rmμmω1tωhω(hω + ht)/2 = (365×314 + 245×0,0037×400×30)[1000 - (30 + 30) : 2] + 1,41×245×0,0014×46×940(940 + 30) : 2 = 131,2 кН×м.
Поскольку M = 131,2 кН×м > M = 130 кН×м, прочность обеспечена.
4. РАСЧЕТ АРМОЦЕМЕНТНЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ ПО ОБРАЗОВАНИЮ ТРЕЩИН
4.1 (4.1). Расчет элементов армоцементных конструкций по образованию трещин, нормальных и наклонных к продольной оси элемента, следует производить в соответствии с требованиями СНиП 2.03.01-84 как для железобетонных конструкций из мелкозернистого бетона соответствующего класса. При этом значение момента сопротивления с учетом трещин Wpl следует определять по п. 4.13, а Rbt, ser принимать без учета коэффициента условий работы бетона γb.
4.2. Расчет элементов армоцементных конструкций по образованию трещин, нормальных и наклонных к продольной оси элемента, следует производить: для выявления необходимости проверки по раскрытию трещин; для выяснения случая расчета по деформациям.
В элементах армоцементных конструкций или на его участках трещины отсутствуют, если усилия, вызванные действием полной нагрузки или ее частью, вводимые в расчет с коэффициентом надежности по нагрузке γ = 1, меньше усилия, которое воспринимает сечение при образовании трещин. Полная нагрузка включает постоянные, длительные и кратковременные нагрузки.
Допускается принимать без расчета, что изгибаемый элемент прямоугольного и таврового сечений с сжатой полкой имеет в наиболее напряженных участках трещины, нормальные к продольной оси, если требуемый по расчету коэффициент армирования больше 0,005.
4.3. Расчет армоцементных элементов по образованию нормальных трещин должен производиться из условия
Mr ≤ Mcrc. (66)
где Mr - момент внешних сил, расположенных по одну сторону от рассматриваемого нормального сечения, относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется; Mcrc - момент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин и определяемый по формуле
Mcrc = Rbt, serWpl ± Mshr. (67)
Здесь Mshr - момент усилия Nshr, вызванного усадкой армоцемента относительно той же оси, что и для определения Mr; знак момента определяется направлением вращения («плюс» - когда направления противоположны, «минус» - когда направления моментов Mshr и Mr совпадают).
Для свободно опертых балок или плит момент Mcrc определяется по формуле
Mcrc = Rbt, serWcrc - Nshr(eON + r). (68)
Усилие Nshr рассматривается как внешняя растягивающая сила, величина и эксцентриситет относительно центра тяжести приведенного сечения которой определяются по формулам:
Nshr = σshr(μ'mf1Afc + μmω1Aω + μmft1Aft); (69)
eON = (μmf1Aftyt + μmω1Aωyω - μm1Afcyc)/(μm1Afc + μmω1Aω + μmf1Aft), (70)
где yt, yω, yc - расстояния от центра тяжести приведенного сечения до центров тяжести сечений соответственно растянутой полки, вертикальной стенки и сжатой полки; σshr - напряжение в сетке (приведенном сетчатом армировании), вызванное усадкой бетона, принимается по табл. 3; μ'mf1, μmω1, μmf1 - коэффициенты армирования, приведенные к сетчатому по отношению модулей упругости соответственно сетчатого для верхней полки, стенки и нижней полки.
Величина Mr определяется по формулам:
для изгибаемых моментов Mr = M;
для внецентренно сжатых элементов
Mr = N(e0 - r); (71)
для центрально и внецентренно растянутых элементов
Mr = N(e0 + r). (72)
Здесь r - расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
Величина r определяется:
для изгибаемых элементов без преднапряжения по формуле
r = Wpl/[(1 + μm(E))Afc + (1 + μmω(E))Aωt + (1 + μmf1(E))Aft]; (73)
для внецентренно сжатых изгибаемых преднапряженных и внецентренно растянутых элементов, если N < P, по формуле
r = φWpl/[(1 + μm(E))Acf + (1 + μmω(E))Aωt + (1 + μmf1(E))Aft]; (74)
где φ = 1,6σb/Rb sec, но принимается не менее 0,7 и не более 1; σb - максимальное напряжение в сжатом бетоне, вычисляемое для упругого тела по приведенному сечению;
для внецентренно растянутых элементов - по формуле (если N > P)
rn = Wpl/[A + 2α(μm(E)A)], (75)
где Wpl - момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый согласно указаниям п. 4.4.
Примечание. Приведенное сечение включает сечение бетона, а также, сечение всей продольной арматуры, умноженное на отношение соответствующих модулей упругости арматуры и бетона.
4.4. Величина момента сопротивления приведенного сечения для крайнего растянутого волокна (с учетом неупругих деформаций растянутого бетона) Wpl определяется в предположении отсутствия продольной силы N и P по формуле
Wpl = 2(Ibc + αImc1 + αImt1)/(h - x) + Sbt, (76)
где Ibc, Imc1, Imt1 - моменты инерции соответственно площадей сечения сжатой зоны бетона, арматуры, расположенной в пределах сжатой зоны и в пределах растянутой зоны относительно нулевой линии; Sbt - статический момент площади сечения растянутой зоны бетона относительно нулевой линии.
Положение нулевой линии в общем случае определяется из условия
S'bc + αS'mc - αSmt = (h - x)Abt/2, (77)
где S'bc, S'mc, Smt - статические моменты соответственно площади сечения сжатой зоны бетона, арматуры, приведенной к площади сеток, расположенной в сжатой зоне и в растянутой зоне сечения; Abt - площадь сечения растянутой зоны бетона, α = Em1/Eb.
Для прямоугольных, тавровых и двутавровых сечений положение нулевой линии может быть определено из выражения
h
- x = ![]() , (78)
, (78)
где ![]() - статический момент
площади приведенного сечения, вычисленный без учета площади бетона растянутых
свесов, относительно крайнего растянутого волокна;
- статический момент
площади приведенного сечения, вычисленный без учета площади бетона растянутых
свесов, относительно крайнего растянутого волокна; ![]() - площадь
приведенного сечения, вычисленная без учета половины площади бетона растянутых
свесов.
- площадь
приведенного сечения, вычисленная без учета половины площади бетона растянутых
свесов.
Значение Wpl для двутавровых сечений допускается определять по формуле
Wpl = [0,292 + 0,75(γ1 + 2μmf1α) + 0,75 (γ2 + 2μ'mf1α)]tωh2, (79)
где γ1 = (bf - tω)tf/(tωh);
γ2 = 2(b'f - tω)t'f/(tωh);
α = Em1/Eb;
μmft = μmf + μsEs/Em1 + μspEsp/Em1;
μ'mf1 = μ'mf + μsEs/Em1 + μspEsp/Em1;
здесь μs, μsp - коэффициенты армирования сечения соответственно ненапрягаемой и напрягаемой стержневой (проволочной) арматуры; μmf, μmω - коэффициенты армирования сечения соответственно растянутой полки и сжатой полки; bf, b'f - ширина полок двутаврового сечения соответственно растянутой и сжатой; tf, t'f - толщина полок двутаврового сечения соответственно растянутой и сжатой; tω - толщина вертикальной стенки двутаврового сечения; h - высота сечения; Es, Em, Eb - модули упругости соответственно арматуры сеток и бетона.
Таблица 13
|
Характеристика сечения |
Коэффициент γ |
Форма поперечного сечения |
|
|
1 |
Прямоугольное |
1,75 |
|
|
2 |
Тавровое с полкой, расположенной в сжатой зоне |
1,75 |
|
|
3 |
Тавровое с полкой (уширением), расположенной в растянутой зоне: |
|
|
|
при bt/bω ≤ 2 независимо от отношения tf/h |
1,75 |
||
|
bf/bω > 2; tf/h ≥ 0,2 |
1,75 |
||
|
bf/bω < 2; tf/h < 0,2 |
1,5 |
||
|
4 |
Двутавровое симметричное (коробчатое) сечение b'f = bf: |
|
|
|
при b'f/tω = bf/tω £ 2 независимо от отношений t'f/h = tf/h |
1,75 |
||
|
при 2 < b'f/tω = bf/tω ≤ 6 независимо от отношений t'f/h = tf/h |
1,5 |
||
|
при b'f/tω = bf/tω > 6 и t'f/h = tf/h ≥ 0,2 |
1,5 |
||
|
при 6 < b'f/tω = bf/tω ≤ 15 и t'f/h = tf/h < 0,2 |
1,25 |
||
|
при b'f/tω = bf/tω > 15 и t'f/h = tf/h < 0,1 |
1,1 |
||
|
5 |
Двутавровое несимметричное, удовлетворяющее условию b'f/bf ≤ 3: |
|
|
|
при bf/tω ≤ 2 независимо от отношения tf/h |
1,75 |
||
|
при 2 < bf/tω ≤ 6 независимо от отношения tf/h |
1,5 |
||
|
при bf/tω > 6; tf/h > 0,1 |
1,5 |
||
|
6 |
Двутавровое несимметричное, удовлетворяющее условию 3 < b'f/bf < 8: |
|
|
|
при bf/tω ≤ 4 независимо от отношения tf/h |
1,5 |
||
|
при bf/tω > 4 и tf/h ≥ 0,2 |
1,5 |
||
|
при bf/tω > 4 и tf/h < 0,2 |
1,25 |
||
|
7 |
Двутавровое несимметричное, удовлетворяющее условию b'f/bf ≥ 8: |
|
|
|
при tf/h > 0,3 |
1,6 |
||
|
при tf/h ≤ 0,3 |
1,25 |
||
|
8 |
Кольцевое и круглое |
2 - 0,4D1/D |
|
|
9 |
Крестовое: |
|
|
|
при b'f/b ≥ 2 и 0,9 ≥ t'f/h > 0,2 |
2 |
||
|
в остальных случаях |
1,75 |
||
|
Примечание. В таблице обозначения bf и tf соответствуют размерам полки, которая при расчете по образованию трещин - растянута, а b'f и t'f - соответствуют размерам полки, которая для этого случая расчета сжата. |
|||
При известном значении W величину Wpl можно также определять по формуле
Wpl = γW, (80)
где γ - коэффициент отношения момента сопротивления W к значению Wpl, определяется по табл. 13; W - момент сопротивления для растянутой грани приведенного сечения, определяемый по правилам сопротивления упругих материалов.
4.5. Расчет по образованию трещин, наклонных к продольной оси, должен производиться из условия
σbt ≤ γbRbt, ser, (81)
где γb - коэффициент условий работы бетона, определяемый по формуле
γb = (1 - σbc/Rbt, ser)/(0,2 + 0,02B). (82)
Здесь B - класс бетона по прочности на сжатие, МПа.
Значения главных растягивающих и главных сжимающих напряжений в бетоне σbt (σbc определяется по формуле)
Напряжения σx, σy и τxy определяются как для упругого тела. Проверка условия (83) производится в центре тяжести приведенного сечения и в местах примыкания сжатых полок и стенке элемента таврового и двутаврового сечения.
РАСЧЕТ АРМОЦЕМЕНТНЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН
4.6. Армоцементные элементы рассчитываются по раскрытию трещин: нормальных к продольной оси элемента; наклонных к продольной оси элемента.
Проверка ширины раскрытия трещин не требуется, если согласно расчету по пп. 4.1 - 4.5 они не образуются от действия постоянных, длительных и кратковременных нагрузок, вводимых в расчет с коэффициентом надежности по нагрузке γt = 1.
При расчете по раскрытию трещин усилие от усадки бетона принимается равным нулю.
4.7. В общем случае расчет по раскрытию трещин производится два раза: на непродолжительное и продолжительное раскрытие.
Для изгибаемых элементов, выполняемых из мелкозернистого бетона при проверке раскрытия трещин, нормальных к продольной оси элемента, допускается расчет производить только один раз, если Me/Mtot ≥ 2×2/3, проверяется продолжительное раскрытие трещин от действия момента Mе, от постоянных и длительных нагрузок; если Me/Mtot < 2/3, проверяется непродолжительное раскрытие трещин от действия момента Mtot от действия постоянных, длительных и кратковременно действующих нагрузок.
РАСЧЕТ ПО РАСКРЫТИЮ ТРЕЩИН, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
4.8. Ширина раскрытия трещин acrc, мм, нормальных к продольной оси элемента, при сетчатом армировании должна определяться по формуле
acrc = ηmφeσmSm/Em1, (84)
где ηm - коэффициент, принимаемый равным при сварных сетках - 3; при тканых - 3,5; φe - коэффициент, принимаемый равным при учете: кратковременных и непродолжительного действия постоянных и длительных нагрузок - 1; продолжительного действия постоянных и длительных нагрузок: для мелкозернистых бетонов группы А-1,5; Б-1,7; В-1,65.
В водонасыщенном состоянии (элементы, воспринимающие давление жидкости, а также эксплуатируемые в грунте ниже уровня грунтовых вод) группы А-1,4; Б-1,6; В-1,4.
σm - напряжения в сетках у растянутой грани сечения от действия нагрузки, определяется согласно п. 4.10; Em - модуль упругости сетки, принимаемый по п. 2.25; Sm - размер ячейки сетки, мм.
4.9. Ширину раскрытия трещин acrc, мм, нормальных к продольной оси элемента, при комбинированном армировании следует рассчитывать по формуле
acrc =
φφeγmηm(σm/Em1)20(3,5 - 100μmt1)![]() , (85)
, (85)
где φ - коэффициент, принимаемый равным: для изгибаемых и внецентренно сжатых элементов - 1, для растянутых элементов - 1,2; φe - коэффициент тот же, что и в п. 4.8; γm - коэффициент, зависящий от величины коэффициента приведенного сетчатого армирования растянутой зоны элемента и принимаемый при:
0,4 % < μm1 < 1 % - 4,5;
1 % ≥ μm1 < 2 % - 3;
μm1 > 2 % - 1,5;
ηm - коэффициент, принимаемый равным:
при сварных сетках - 0,8;
при тканых сетках - 1;
σm - напряжение в сетчатой арматуре принимается по п. 4.10; μmt1 - коэффициент приведенного армирования растянутой зоны, принимаемый в формуле (85) не более 0,02; ds - диаметр стержневой или проволочной арматуры, мм; при различных диаметрах стержней и проволоки сеток значение ds принимается равным:
ds = (n1d21 + … + nkd2k)/(n1d1 + ... + nkdk), (86)
d1, …, dk - диаметр стержней, проволок растянутой арматуры; n1, …, nk - число стержней, проволок; Em1 - приведенный модуль упругости арматуры, определяемый по формуле
Em1 = (Emμm + Esμs)/(μm + μs). (87)
4.10. Напряжение σm следует определять:
а) в центрально-растянутых элементах
где P - усилие предварительного напряжения с учетом всех потерь; Ab - площадь сечения бетона;
б) для изгибаемых, внецентренно сжатых или внецентренно растянутых элементов - по правилам строительной механики как для упругого тела.
В расчете σm должно рассматриваться сечение, приведенное к эквивалентному стальному сечению (см. рис. 36), с единой упругой характеристикой; в растянутой зоне к стальному сечению приводится только арматура с эквивалентной площадью сечения, а в сжатой зоне - арматура и бетон с эквивалентными площадями сечения (бетон - с учетом отношения модулей упругости).
Значение σm определяется:
для изгибаемых элементов - по формуле
σm = [M - P(ecp + r)]/Ws1; (89)
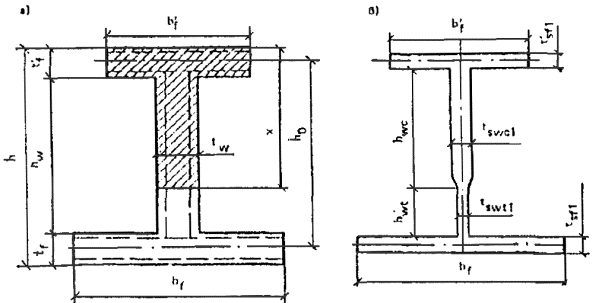
Рис. 36. Схема приведения сечений армоцементных элементов к стальному
а - сечение армоцементного элемента; б - сечение, приведенное к стальному
для внецентренно сжатых и внецентренно растянутых элементов - по формуле
σm = Ntot(ec, tot ± r)/Ws1, (90)
где Ws1 - момент сопротивления приведенного к стальному сечению определяется по формуле
Ws1 = Is1/1,3yc. (91)
Здесь Is1 - момент инерции сечения, приведенного к эквивалентному стальному сечению, относительно его центра тяжести; Ntot - равнодействующая продольной оси N и усилия предварительного обжатия P;
ec, ecp - эксцентриситеты приложения сил соответственно N и P относительно центра тяжести сечения элемента: ec, tot - эксцентриситет усилия Ntot относительно центра тяжести сечения; r - расстояние от ядровой точки до ближайшей сжатой грани сечения.
В формуле (90) напряжений в сетке внецентренно сжатых элементов знак «минус» принимается при внецентренном сжатии, а знак «плюс» - при внецентренном растяжении.
4.11 (4.6). Для элементов, к трещиностойкости которых предъявляются требования 2-й категории, ширина непродолжительного раскрытия трещин определяется как сумма ширины раскрытия от продолжительного действия постоянных и длительных нагрузок и приращения ширины раскрытия от действия кратковременной нагрузки. Ширина продолжительного раскрытия трещин зависит от продолжительности действия постоянных и длительных нагрузок.
4.12. Ширина непродолжительного раскрытия трещин от действия полной нагрузки определяется как сумма ширины раскрытия от продолжительного действия постоянных и длительных нагрузок и приращения ширины раскрытия трещин от действия кратковременной нагрузки по формуле
acrc = acrc1 - acrc2 + acrc3, (92)
где acrc1 - ширина раскрытия трещин от непродолжительного действия всей (полной нагрузки); acrc2 - начальная ширина раскрытия трещин от постоянных и длительных нагрузок (при их непродолжительном действии); acrc3 - ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок.
В изгибаемых элементах непродолжительное раскрытие трещин от полной нагрузки может определяться по формуле
acrc = acrc1[1 + (φe - 1)Me/Mtot], (93)
где φe - см. п. 4.8 для случая продолжительного действия нагрузки.
Ширина продолжительного раскрытия трещин определяется от действия постоянных и длительных нагрузок.
РАСЧЕТ ПО РАСКРЫТИЮ ТРЕЩИН, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
4.13. Ширина раскрытия трещин, наклонных к продольной оси изгибаемых элементов, при сетчатом и комбинированном армировании определяется по формуле
acrc = φeK1(hω + 30dm)]ηmK22/μmω1E2m, (94)
где φe - коэффициент тот же, что и в п. 4.8; K1 - коэффициент, принимаемый:
при тканых сетках - 103(30 - 1500μm1);
при сварных сетках - 103(20 - 1200μm1);
ηm - коэффициент тот же, что и в п. 4.8; μmω1 - принимается согласно указаниям п. 3.2; dm - диаметр проволок сеток, расположенных по нормали к продольной оси элемента;
K2 = Q/(tωhω) - 0,25Np/Ab. (95)
Здесь Q - наибольшая поперечная сила на рассматриваемом участке длины элемента от действия нагрузки.
При определении ширины раскрытия наклонных трещин от непродолжительного и продолжительного действия нагрузки должны учитываться указания п. 4.12.
ПРИМЕРЫ РАСЧЕТА
Пример 20.
Дано. Армоцементная складчатая плита покрытия шириной 3, высотой 0,5 м, пролетом 9,2 м (рис. 37). Бетон мелкозернистый класса В40. По условиям эксплуатации конструкция отвечает требованиям 2-й категории трещиностойкости. Расчетные и нормативные характеристики стали: тканой сетки № 10-1 - ГОСТ 3826-82*: Em = 1,5×105 МПа; сварной сетки из арматурной проволоки класса Вр-I диаметром 4 мм: Rs = 370 МПа, Rsω = 265 МПа, Rsc = 365 МПа, Es = 1,7×103 МПа; стержневой арматуры класса А-III диаметром 6 мм (табл. 10 и 20): Rs = 355 МПа, Rsω = 285 МПа, Rsc = 355 МПа, Es = 2×103 МПа.
Расчетные (при коэффициенте условий работы γb1 = 1) и нормативные характеристики мелкозернистого бетона класса В40 (табл. 6 - 8 и 10): Rb = 22 МПа, Rbt = 1,35 МПа, Rb, ser = 29 МПа, Rbt, ser = 1,76 МПа, Eb = 2,4×104 МПа.
Усилия от нагрузок расчетной M = 106600 Н×м, Q = 47700 Н, полной нормативной M = 87400 Н×м, Q = 39000 Н, нормативно длительно действующей M = 66500 Н×м.
Коэффициент армирования сжатой полки (приведенный к сетчатому) μmf1 = 0,0182, стенки (при двух слоях сетки) μmω1 = μmω = 0,0047, растянутой полки (приведенный к сетчатому) μmf1 = 0,0485.
Требуется произвести расчет по ширине раскрытия трещин, нормальных к продольной оси элемента.
Коэффициенты приведенного армирования с учетом модулей упругости равны:
сжатой полки
μ'mf1(E) = μm + μsEs/Em = 0,0047 + 0,0075×2×105 : (1,5×105) = 0,0147;
стенки
μmω1(E) = μmω = 0,0047;
растянутой полки
μmf1(E) = μm + μsEs/Em = 0,0047 + 0,0314×2×105 : (1,5×105) = 0,0465.
Отношение модулей упругости
α = Em/Eb = 1,5×105/2,4×104 = 6,25.
Приведенная площадь сечения
A1 = 90×3(1 + 6,25×0,0147) + 30,3×44(1 + 6,25×0,0047) + 150×3(1 + 6,25×0,0465) = 2149 см2.
Статический момент приведенной площади сечения относительно нижней грани
S1 = 90×3(1 + 6,25×0,0147)(50 - 3/2 + 30,3×44(1 + 6,25×0,0047)(50 - 3 - 44/2) + 150,3(1 + 6,25×0,0465)3/2 = 44697 см3.
Расстояние от центра тяжести до нижней грани ycm = S1/A1 = 44697/2149 = 20,8 см.
Момент инерции сечения относительно центра массы приведенного сечения
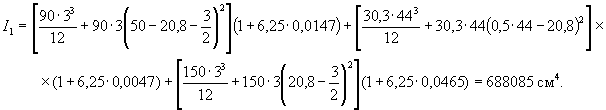 Согласно табл. 13, при отношениях 3 > b'f/tω = 90/30,3 = 2,97; 2
< bf/tω = 150/30,3 = 4,95 <
6 коэффициент γ = 1,5.
Согласно табл. 13, при отношениях 3 > b'f/tω = 90/30,3 = 2,97; 2
< bf/tω = 150/30,3 = 4,95 <
6 коэффициент γ = 1,5.
Рис. 37. Сечения армоцементной складчатой плиты покрытия
а - поперечное; б - расчетное; в - одной волны с армированием
Пластический момент сопротивления приведенного сечения
Wpl = γI1/ycm = 1,5×688085 : 20,8 = 49621 см3.
Расстояние от центра тяжести массы приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется по формуле (73), равно:
rn = 688085/20,8(1 + 6,25×0,0147)90×3 + (1 + 6,25×0,0047)30,3744 + (1 + 6,25×0,0465)150,3 = 15,4 см.
Эксцентриситет по формуле (70) равен:
eON = (0,0485×150,3×19,3 + 0,0017×30,3×4,2 - 0,0182×90×3×29,2)/(0,0182×90×3 + 0,0017×30,3×41 + 0,0185×150×3) = 9,2 см
и нормальная сила от деформации усадки по формуле (60) равна:
Nshr = 52(0,0182×90×3 + 0,0047×30,3×44 + 0,0485×150×3) = 171,6 кН.
Момент, воспринимаемый нормальным сечением при образовании трещин по формуле (68), равен:
Mcrc = 1,76×49621 - 171,6(9,2 + 15,4) = 62138 Н м.
Так как Mcrc = 62138 Н×м < M = 87400 Н×м, то в стадии эксплуатации трещины возникают.
Приведенный модуль упругости сжатой арматуры по формуле (87) равен:
Emc1 = (1,5×105×0,00447 + 2×105×0,0075)/(0,0047 + 0,0075) = 1,805×105 МПа;
то же, растянутой арматуры по формуле (87) равен:
Emf1 = (1,5×105×0,0047 + 2×105×0,0314)/(0,0047 + 0,0314) = 1,93×105 МПа.
Вычисление напряжений в арматуре производим в соответствии с п. 4.10. Высота растянутой полки в сечении, приведенном к стальному, равна:
tsf1 = 0,0147×3 + 3×2,4×104/(1,805×105) = 0,443 см.
Высота сжатой полки tsf1 = 0,0465×3 = 0,14 см. Толщина стенки в сжатой зоне tscω1 = 0,0047×30,3 + 30,3(2,4×104/1,5×105) = 4,99 см. Толщина стенки в растянутой зоне tstω1 = 0,0047×30,3 = 0,143 см.
Высота сжатой зоны в момент трещинообразования
x1 = h - S1/(A + A1/2) = 50 - 48747/(1761 + 463/2) = 25,5 см.
Площадь сечения, приведенного к стальному, As1 = 90×0,443 + 4,99×25,057 + 0,143×21,66 + 150×0,14 = 189 см2. Статический момент относительно нижней грани сечения Ss1 = 90×0,443(47,3 - 0,443/2) + 4,99×25,057(47,3 - 0,443 - 25,057/2) + 0,143×21,66(0,14 + 21,66/2) + 150×0,14(0,14/2) = 6204 см3. Расстояние от центра тяжести сечения до нижней грани y = Ss1/Fs1 = 6204/189 = 32,8 см.
Момент инерции сечения, приведенного к стальному, относительно центра тяжести сечения равен:
Is1 = 90×0,4433/12 + 90×0,443×14,282 + 4,99×25,0573/12 + 4,99×25,057×1,752 + 0,143×21,663/12 + 0,143×21,66×21,92 + 150×0,143/12 + 150×0,14×32,732 = 39880 см4.
Момент сопротивления Ws1 = Is1/1,3y = 39880/1,3×32,8 = 935 см3. Напряжение от кратковременного действия полной нагрузки в растянутой зоне по формуле (89) равно:
σm = M/Ws1 = 87400/935 = 93,5 МПа,
то же от постоянно действующей нагрузки σm = 66500/935 = 71,1 МПа.
Ширину непродолжительного раскрытия трещин от действия полной нагрузки определяем в соответствии с п. 4.12:
acrc = acrc1 - acrc2 + acrc3.
Ширина раскрытия трещин от непродолжительного действия всей (полной) нагрузки по формуле (85)
acrc1 =
φφeγmηm(σm/Em1)20(3,5
- 100μmf1)![]() = 1×1×1,5×1×93,5
: (193×105)20(3,5
- 100×0,02)
= 1×1×1,5×1×93,5
: (193×105)20(3,5
- 100×0,02)![]() = 0,01 мм.
= 0,01 мм.
Ширина раскрытия трещин от постоянных и длительных нагрузок (при их непродолжительном действии) по формуле (85)
acrc2 = 1×1×1,5×1![]() 20(3,5 - 100×0,02)
20(3,5 - 100×0,02)![]() = 0,03 мм.
= 0,03 мм.
Ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок по формуле (85)
acrc3 = 1×1,5×1,5×1![]() 20(3,5 - 100×0,02)
20(3,5 - 100×0,02)![]() = 0,05 мм.
= 0,05 мм.
Таким образом, ширина непродолжительного раскрытия трещин acrc = 0,04 - 0,03 + 0,05 = 0,06 мм < 0,2 мм (см. табл. 1).
Ширина продолжительного раскрытия трещин
acrc3 = 0,03 мм < 0,15 мм,
т.е. по ширине раскрытия трещин рассчитываемое сечение конструкции соответствует требованиям 2-й категории трещиностойкости.
Пример 21.
Дано. Стенка армоцементной емкости для хранения сыпучих материалов толщиной δ = 25 мм выполнена из мелкозернистого бетона класса В40. Стенка армируется:
шестью слоями сварных сеток для армоцемента № 12-0,7 по ТУ 14-4-113-76;
сварной сеткой из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I, Æ = 6, шаг 100 мм.
Расчетные и нормативные характеристики - холодной проволоки класса Вр-I: Rs = 375 МПа, Es = 170000 МПа, сварных сеток № 12-0,7, Rm = 245 МПа, Em = 150000 МПа. Осевое усилие растяжения стенки N = 55 кН.
Требуется выполнить расчет по ширине раскрытия трещин.
Коэффициент армирования
μm = 6μ/t = 6×0,0031 : 2,5 = 0,00744.
Коэффициент армирования сварными сетками из холоднотянутой проволоки (на участке стенки высотой h = 1 м)
μs = As/(th) = 10×0,283 : (2,5×100) = 0,0113.
Коэффициент приведенного армирования
μm1 = μm + μsRm/Rs = 0,0074 + 0,0113×375 : 245 = 0,0247.
Ширина раскрытия трещин, нормальных к продольной оси элемента, при сетчатом армировании определяется по формуле (84):
acrc = ηmφeσmSm/Em,
где ηm = 3; φe = 1,5.
Напряжение в сетках у растянутой грани согласно п. 4.10 для центрально-растянутых элементов по формуле (88)
σm = (N - P)/(μm1Ab, tot) = 550000 : (0,025×2500) = 88 МПа.
Усилие предварительного напряжении P равно нулю. Площадь бетона равна Abtot = 100×25 = 2500 мм2. Приведенный модуль упругости по формуле (87)
Em1 = (170000×0,0113 + 150000×0,00744)/(0,0113 + 0,0074) = (1921 + 1110)/0,0184 = 164728 МПа.
Ширина раскрытия трещин по формуле (84)
acrc = 3×1,5×88/164728×12 = 0,028 мм < 0,05 мм (табл. 1).
Для заданных условий эксплуатации в соответствии с табл. 1 такое раскрытие трещин допускается.
Пример 22.
Дано. Армоцементная складчатая плита покрытия (рис. 38) с расчетным пролетом 5,95 м армируется:
двумя ткаными сетками № 10-1 по ГОСТ 3826-82* (коэффициент сетчатого армирования при одном слое сетки на 1 см толщины составляет μm = 0,0071);
сварными сетками из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I по ТУ 14-4-713-76 (в сжатой зоне - восемь стержней диаметром 3 мм, As = 8×7,1 = 57 мм2; в растянутой зоне - 28 стержней диаметром 4 мм, As = 28×12,6 = 3,53 мм2).
Изгибающий момент от продолжительно действующей нагрузки Me = 19,82 кН×м, полный момент в середине пролета Mtot = 30,1 кН×м. Расчетные сопротивления и модули упругости арматуры и бетона принимаются: для тканой сетки Rm = 245 МПа, Em = 150000 МПа; для сварной сетки из стальной низкоуглеродистой холоднотянутой проволоки Rs, ser = 410 МПа, Es = 170000 МПа; для мелкозернистого бетона класса В40 группы А - Rb, ser = 29 МПа, Rbt, ser = 2,1 МПа, Eb = 28,5×103 МПа.
Требуется произвести расчет по раскрытию трещин, нормальных к продольной оси элемента.
Расчет. Толщина вертикальной стенки приведенного двутаврового сечения
tω = tfn/sinβ = 20×8/sinβ = 165,5 мм.
Площадь сечения плиты
Ab = 920×20 + 1950×165,5 + 1840×25 = 800400 мм2.
Коэффициент приведенного армирования
μ'm1 = μm + μ'sRs/Rm = 0,0071 + 0,0031×410 : 245 = 0,0123.
Коэффициент армирования стенки при двух слоях сетки
μω = 2μ/tω = 2×0,0071/2 = 0,0071.
Коэффициенты армирования растянутой полки сечения тканой и сварной сетками из стальной низкоуглеродистой холоднотянутой проволоки соответственно равны:
μm = 2μ/tf = 2×0,0071/2,5 = 0,00567;
μs = As/bftf = 353/1840×25 = 0,00767,
а коэффициент приведенного армирования
μm1 = μm + μsRs/Rm = 0,00567 + 0,00767×410 : 245 = 0,0185.
Рис. 38. Сечения складчатой плиты перекрытия
а - поперечное; б - приведенное расчетное
Приведенные модули упругости по формуле (87) равны:
растянутой полки
![]()
сжатой полки
![]()
Коэффициенты приведенного армирования с учетом отношений модулей упругости равны:
в сжатой полке
μ'(E)1 = μ'm + μ'sEs/Em = 0,0071 + 0,0031×170000 : 150000 = 0,0106;
в растянутой полке
μ(E)1 = μm + μsEs/Em = 0,00567 + 0,00767×170000 : 150000 = 0,0144;
μω(E)1 = μω = 0,0071.
Определяем размеры сечения, приведенного к стальному. Высота сжатой полки
t'sf1 = μ'(E)1t'f + t'fEb/E'1 = 0,0106×20 + 20×28500 : 156000 = 3,852 мм.
Высота растянутой полки
tsf1 = μ(E)1tf = 0,0144×25 = 0,36 мм.
Толщина стенки в сжатой зоне (с учетом бетона)
t'sω = μ'm(E)1tω + t'ωEb/Em = 0,0071×165,5 + 165,5×28500 : 150000 = 31,62 мм.
Толщина стенки в растянутой зоне
tsω = μm(E)1tω = 0,0071×165,5 = 1,14 мм.
Для определения положения нейтральной оси в момент трещинообразования вычисляем статический момент площади таврового сечения (без учета свесов в растянутой зоне) относительно нижней грани, который равен:
![]() =
92×2(24
- 2/3)(1 + 5,26×0,0106)103 + 16,55(19,5 + 25)
=
92×2(24
- 2/3)(1 + 5,26×0,0106)103 + 16,55(19,5 + 25)![]() (1 + 5,26×0,0071)103
= 8622,63×103 мм3.
(1 + 5,26×0,0071)103
= 8622,63×103 мм3.
Отношение модулей α = Em/Eb = 150000/28500 = 5,26. Приведенная суммарная площадь Ab таврового сечения
Ab = b'ft'f(1 + n1μ'(E)1) + tω(hω + tf)(1 + n1μω) = 92×2(1 - 5,26×0,0106)102 + 16,55(19,5 + 2,5)102(1 + 5,26×0,0071)102 = 551,44×102 мм2.
Площадь свесов растянутой полки
At = (184 - 16,55)2,5(1 + 5,26×0,0144)102 = 450,33×102 мм2.
Расстояние центра тяжести относительно растянутой грани сечения
h - x = Sb/(Ab + Aft/2) = 8622,63×103 : (551,44 + 45033 : 2) = 111,03 мм.
Высота сжатой зоны для упругопластического состояния сечения x = h - 111,03 = 240 - 111,03 = 129 мм.
Статический момент сечения, приведенного к стальному относительно нижней грани сечения, равен:
S1 = 92×0,38×21,75 + 3,16×10,9×15,3 + 9,848×0,114×49,25 + 184×0,036×0,036/2 = 1392,37×103 мм3.
Площадь приведенного стального сечения
As1 = 92×0,38 + 10,9×3,16 + 9,85×0,114 + 184×0,036 = 76,62×102 мм2.
Расстояние от центра тяжести этого сечения до нижней грани
yc = S1/As1 = 1392,37 : 76,62 = 181,7 мм.
Момент инерции сечения, приведенного к стальному, относительно центра тяжести сечения равен:
Is = 92×0,382/12 + 92×0,38×3,582 + 3,2×10,92/12 + 3,2×10,9×2,872 + 0,114×9,853/12 + 0,114×9,85×13,242 + 184,0×0,363/12 + 184,0×0,036×18,72 = 3459,14×104 мм4.
Момент сопротивления сечения, приведенного к стальному, равен
Ws1 = Is1/1,3ys = 3459,14×104 : (1,3×181,7) = 146,44×103 мм3.
Напряжение σm для изгибаемых элементов
σm = M/Ws1 = 30100000 : (146,44×103) = 205,54 МПа.
Отношение Mc/Mtot = 19820000/30100000 = 0,658 < 2/3 = 0,666, следовательно, на основании п. 4.7 проверяется непродолжительное раскрытие трещин от действия момента M.
Ширина раскрытия трещин, нормальных к продольной оси элемента при смешанном армировании, вычисляется по формуле (85):
acrc = φφeγmηm(σm/Em1)20(3,5
- 100μmt1)![]() ,
,
где для изгибаемых элементов φ = 1; φe = 1; γm = 3, так как 1 % < μm1 < 2; ηm = 1 для тканых сеток; μmt1 = 0,0185.
Приведенный диаметр стержневой и проволочной арматуры ds по формуле (86) равен:
ds = (28,42 + 370×1)/(28×4 + 370×1) = 1,7 мм; Em1 = 161500 МПа.
После подстановки в формулу (85) полученных величин ширина раскрытия трещин
acrc = 1×1×3×1×205,54×20/161500(3,5
- 100×0,0185)![]() = 0,15 мм.
= 0,15 мм.
По табл. 1 предельная ширина кратковременного раскрытия трещин допускается acrc1 = 0,15 мм.
Пример 23.
Дано. Армоцементный элемент с приведенным двутавровым сечением h = 280 мм, с размерами верхней полки b'f = 250 мм, t'f = 20 мм; нижней полки bf = 740 мм, tf = 20 мм; высоты стенки hω = 240 мм и толщины стенки tω = 56 мм. Сечение армируется: двумя слоями тканых сеток № 8-07 по ГОСТ 3826-82* (μm = 0,0044 при одной сетке на 10 мм толщины стенки); ненапрягаемая арматура в виде сеток из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I (четыре проволоки диаметром 3 мм). Расчетные и нормативные характеристики сварной сетки Rm = 245 МПа, Em = 150000 МПа. Мелкозернистый бетон класса В35 группы А. Расчетное сопротивление Rb = 19,5 МПа, Rbt = 1,3 МПа, Eb = 27500 МПа. Сварные сетки из проволоки класса Вр-I, Æ = 3 мм с расчетным сопротивлением Rs = 375 МПа, Es = 200000 МПа.
Изгибающий момент в сечении M = 6,56 кН×м. Требуется рассчитать поперечное сечение армоцементной складчатой плиты по образованию трещин.
Коэффициенты армирования равны:
ткаными сетками
μmf = μmω = μmc = 0,0044×2 : 2 = 0,0044;
сжатой полки, армированной сварными арматурными каркасами,
μ's = A's/A'f = 2828 : (250×20) = 0,0057;
растянутой полки
μs = As/Af = 28,28 : (740×20) = 0,0019.
Напряжение в сетке σshr вызванное усадкой бетона для мелкозернистого бетона группы А класса В35, равно: σshr = 65 МПа (бетон естественного твердения); усилие Nshr от усадки бетона как внешняя растягивающая сила по формуле (69) равно:
Nshr = 65(0,013×500 + 0,0044×13440 + 0,0073×14800) = 15091,6 Н = 15091,6 кН.
Коэффициент приведенного армирования с учетом отношения модулей упругости:
для сжатой полки
μmt1 = μm + μ'sEs/Em = 0,0044 + 0,0057×200000 : 150000 = 0,012;
для стенки и растянутой полки
μω(E) = μm = 0,0044.
Положение нулевой линии в общем случае определяется по формуле (77)
S'bc + αSmc - αSmt = (h - x)Abt/2;
4155872 = 4924504 - 17551,8x; x = 43,2 мм.
После нескольких приближений находим положение нулевой линии, проходящей через центр тяжести сечения ycm = 123 мм, тогда x = 280 - 123 = 157 мм.
Статический момент площади бетона сжатой зоны
Sbc = 250×30(280 - 123 - 20/2) + (240 + 20 - 123)56(240 + 20 - 123)/2 = 1260532 мм3.
Статический момент площади арматуры сжатой зоны
Smc = 5,25×250×20×0,012(280 - 123 - 20/2) + (240 + 20 - 123)56×0,0044(240 + 20 - 123)/2 = 58444,8 мм3.
Статический момент площади арматуры растянутой зоны
Smt = 5,25×740×20×0,0069(123 - 20/3) + (123 - 20)56×0,0044(123 - 20)/2 = 67414,7 мм3.
Площадь бетона растянутой зоны
Abt = 740×20 + (123 - 20)56 = 20568 мм2.
Полученные значения подставляем в формулу (77) для проверки принятого положения нулевой линии и получаем
1260532 + 58444,8 - 67444,8 @ (280 - 157)/2×20568;
расхождение составляет 1 %, поэтому принимаем x = 157 мм.
Моменты инерции Ibc, Imc1, Imt - соответственно площади сечения сжатой зоны бетона, арматуры и арматуры, расположенной в пределах сжатой зоны, относительно нулевой линии равны:
Ibc = 250×203/12 + 250×20(157 - 20/2)2 + 56(157 - 20/2)3/12 + 56(157 - 20/2)3/2 = 167506000 мм4;
Imc = [250×203/12 + 250×20(157 - 20/2)2]0,012 + [56(157 - 20/2)3/12 + 56(157 - 20/2)(157 - 20/2/2]0,0044 = 1559436 мм4;
Imt = [740×203/12 + 740×20(280 - 157 - 20/2)2]0,0069 + [56(280 - 157 - 20/2)3/12 + 56(280 - 157 - 20/2)3/2]0,0044 = 1425881 мм4.
Статический момент площади сечения растянутой зоны бетона относительно нулевой линии
Sbt = bftf(h - x - tf/2) + tω(h - x - tf)[(h - x - tf)/2] = 740×20(280 - 157 - 20 : 2) + 56(280 - 157 - 20)[(280 - 157 - 20) : 2] = 1969452 мм3.
Момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого волокна по формуле (76)
Wpl = 2(Ibc + αImc1 + αImt1)/(h - x) + Sbt = 2(167506×500 + 5,26×1559436 + 5,26×1425881) : (280 - 157) + 1969452 = 4948443,3 мм3.
Момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого волокна по формуле (79) равен:
γ1 = (bf - tω)tf/(tωh) = (740 - 56)20 : (56×280) = 0,8724;
γ2 = 2(b'f - tω)t'f/(tωh) = 2(250 - 56)20 : (56×280) = 0,4949;
α = Em/Eb = 5,26;
Wpl = 0,292 + 0,75(γ1 + 2μmf1 + α) + 0,0075(γ2 + 2μmft + α)tωh2 = 0,292 + 0,75(0,8724 + 2×0,013×5,26) + 0,075(0,4949 + 2×0,0073×5,26)56×28 = 4768413 мм3
(расхождение равно 36 %).
Для вычисления радиуса инерции rn подставим полученные величины в формулу (73); получим
rn = 4948×443/[(1 + 0,012)5000 + (1 + 0,0044)13440 + (1 + 0,0069)14800] = 4948443 мм4/33461 мм2 = 147,89 мм2.
Момент трещинообразования для свободно опертых балок или плит по формуле (68)
Mcrc = 1,25×4948443 - 15,09(13 + 147,9) = 6185553,7 - 2427,98 = 6183125,8 = 6,183 кН×м.
Изгибающий момент в сечении M = 6 кН×м < Mcrc = 6,183 кН×м. Трещиностойкость элемента обеспечена.
Пример 24.
Дано. Армоцементный складчатый элемент имеет приведенное двутавровое сечение. В сечении действует изгибающий момент M = 200 кН×м, продольная сила N = 800 кН. Ширина верхней и нижней горизонтальных полок: b'f = bf = 400 мм, толщина t'f = tf = 30 мм, толщина вертикальной стенки tω = 46 мм и высота hω = 940 мм. Высота всего сечения h = 1000 мм. Складчатый элемент армируется восемью сварными сетками № 12,5-0,5 ТУ 14-4-713-76 в сжатой и растянутой полках сечения, четырьмя сварными сетками № 12,5-05 по ТУ 14-4-713-76 в наклонных гранях сечения, сварными плоскими каркасами из арматуры диаметром 10 мм класса А-III в сжатой и растянутой полках A's = As = 78,5×4 = 314 мм2 (см. рис. 34).
Расчетные сопротивления и модули упругости: для сварных сеток Rm = Rmc = 245 МПа; Em = 150000 МПа; для арматуры класса А-III по СНиП 2.03.01-84 Rs = Rsc = 369 МПа, Es = 200000 МПа.
Для мелкозернистого бетона группы А класса В35 прочность на осевое сжатие Rb = 18 МПа (Rb, ser = 25,5 МПа), прочность на осевое растяжение Rbt = 1,3 МПа, Rbt, ser = 1,56 МПа при коэффициенте условий работы γb1 = 1.
Начальный модуль упругости Eb = 27500 МПа.
Требуется определить, какой изгибающий момент будет предельным моментом трещинообразования при условии, что отношение M/N сохраняется.
Приведенная расчетная толщина вертикальной стенки таврового приведенного сечения (при угле наклона стенки к вертикали β = 59°54') равна:
tω = 2t/sinβ = 2×20 : 0,865 = 46 мм.
Отношение модулей упругости сеток и бетона
α = Em/Eb = 150000 : 27500 = 5,45.
Коэффициенты армирования сварными сетками равны:
сжатой и растянутой полок при одной сетке на 1 см толщины μm = 0,0014
μmc = μmt = μmh/t'f = 4,0014×8 : 3 = 0,0037;
вертикальной стенки
μmω = μmh/tω = 0,0014×4 : 2 = 0,0028.
Коэффициент армирования сжатой и растянутой полок стержневой арматурой
μ's = μs = As/(b'ft'f) = 314 : (400×30) = 0,026.
Коэффициенты приведенного армирования сжатой и растянутой полок равны:
μmc1 = μmc + μ'sRs/Rm = 0,0037 + 0,026×365 : 245 = 0,042;
μmt1 = μmt + μsRs/Rm = 0,0037 + 0,026×365 : 245 = 0,042.
Коэффициенты приведенного армирования с учетом отношений модулей упругости равны:
для сжатой и растянутой полок
μ = 0,0037 + 0,026×200000/150000 = 0,0384;
для вертикальной стенки
μmω(E) = μmω = 0,0028.
Расчет по образованию нормальных трещин производится из условия (66) Mr ≤ Mcrc. Для внецентренно сжатых элементов (71)
Mr = N(e0 - rn).
Момент инерции приведенного сечения
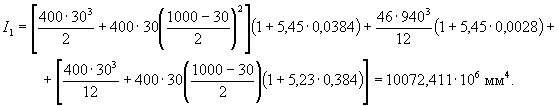
Момент сопротивления
W = 10072,411×106/500 = 20,144×106 мм3.
Площадь сечения
Ab = 400×30(1 + 5,45×0,0384) + 940,46(1 + 5,45×0,0028) + 400×30(1 + 5,45×0,0384) = 72923 мм2.
Напряжение в бетоне
σb = N/Ab + M/Wpl = 800000 : 72923 + 200000000 : 20144000 = 20,9 МПа.
Коэффициент φ = 1,6 - 20,9/25,5 = 0,78. Площадь сжатой полки
Acf = b'ft'f = 12000 мм2.
Площадь стенки
Aωt = tωhω = 46×940 = 43240 мм2.
Площадь растянутой полки Aft = bftf = 12000 мм2. Величину r для внецентренно сжатых элементов определяем по формуле (74).
Значение Wpl для двутаврового сечения определяем по формуле (79)
Wpl = [0,292 + 0,75(γ1 + 2μmftα) + 0,075(γ2 + 2 μ'mftα)]tωh2 = [0,292 + 0,75(0,23 + 2×0,038×5,45) + 0,075(0,23 + 2×0,0384×5,45)]46×10002 = 38044760 мм3,
где
γ1 = (bf - tω)tf/(tωh1) = (400 - 46)30 : (46×1000) = 0,23;
γ2 = 2(b'f - tω)t'f/(tωh) = 2(400 - 46)30 : (46×1000) = 0,23.
Расстояние от центра приведенного сечения до ядровой точки по формуле (74)
![]()
Эксцентриситет продольной силы
ec = M/N = 200 : 800 = 0,25 м.
Mr = N(e0 - rn) = 800(0,25 - 0,435) = 148 кН×м.
Усилие Nshr, вызванное усадкой армоцемента и определяемое по зависимости (69), равно:
Nshr = σshr(μmc1Acf + μmω1Aωt + μmf1Aft) = 52(0,0384×12000 + 0,0028×48240 + 0,0384×12000) = 54946,9 Н,
где в соответствии с рекомендациями п. 4.3 напряжение в сетке, вызванное усадкой бетона, принимаем равным для мелкозернистого бетона группы А класса В35 σshr = 52 МПа (бетон естественного твердения).
Эксцентриситет продольного усилия от усадки Nshr по формуле (70)
![]()
Момент, воспринимаемый нормальным сечением с образованием трещин по формуле (67)
Mcrc = 1,56×38044760 - 54946,9(+434,6) = 35,469903 = 35 кН×м.
Поскольку Mr = 148 кН×м > Mcrc = 35,5 кН×м, трещиностойкость элемента обеспечена.
Пример 25.
Дано. Стенка армоцементной емкости для хранения сыпучих материалов толщиной t = 25 мм, выполнена из мелкозернистого бетона группы А класса В25. Расчетное сопротивление на осевое сжатие Rb = 18,5 МПа. Расчетное сопротивление для предельных состояний второй группы Rbt, ser = 1,35 МПа. Начальный модуль упругости бетона Eb = 21500 МПа. Стенка армируется шестью слоями сварных сеток № 12,5-05 - ТУ 14-4-713-76 сварной сеткой из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I, Æ = 5 мм, шаг 50 мм. Расчетные характеристики арматуры сварных сеток Rm = 245 МПа, Em = 150000 МПа. Сварных сеток из арматуры класса Вр-I: Rs = 360 МПа, Es = 170000 МПа.
Осевое усилие в стенке, длительно действующее, N = 66 кН на 1 м.
Требуется рассчитать сечение нейтрально растянутой стенки по ширине раскрытия трещин.
Коэффициенты армирования сварной сеткой (при коэффициенте сетчатого армирования при одном слое сетки на 1 см толщины элемента, равном μ = 0,0014) равны:
μm1 = 6μm/tω = 6×0,0014 : 2,5 = 0,0034.
Коэффициент армирования сварными сетками из стали класса Вр-I
μs = As/Ab = 20×19,625 : (25×1000) = 0,0157.
Коэффициент приведенного армирования
μmt1 = μmt + μsRs/Rm = 0,0034 + 0,0157×360 : 245 = 0,026.
Напряжение σm, определяемое в соответствии с п. 4.10 для центрально-растянутых элементов, равно:
σm = (N - P)/(μmAb, tot) = 66000 : (0,026×25×1000) = 101,54 МПа.
Приведенный модуль упругости арматуры по формуле (87)
Em1 = (Emμmt + Esμs)/(μmt + μs) = (150000×0,0034 + 170000×0,0157) : (0,0034 + 0,0157) = 166439 МПа.
Диаметр арматуры, приведенный по формуле (86), равен:
ds = (n1d21 + … + nkd2k)/(n1d1 + ... + nkdk) = (100×6×0,52 + 20×52) : (100×6×0,5 + 20×5) = 1,63 мм.
Ширина раскрытия трещин acrc при коэффициентах в соответствии с п. 4.9: φ = 1,2; φe = 1,5; γ = 1,5; γm = 0,8 равна:
acrc = φφeγmηm(σm/Em1)20(3,5
- 100μmt1)![]() = 1,2×1,5×1,5×0,8×101,5
: 166439×20(3,5 - 100×0,026)
= 1,2×1,5×1,5×0,8×101,5
: 166439×20(3,5 - 100×0,026)![]() = 0,06 мм.
= 0,06 мм.
Ширина раскрытия трещин допустима.
Пример 26.
Дано. Складчатый свод покрытия из двух складок имеет приведенное сечение со следующими размерами: ширину верхней полки b'f = 800 мм, толщину t'f = 30 мм, ширину нижней полки bf = 800 мм, толщину tf = 30 мм, высоту сечения h = 1000 мм и толщину стенки tω = 22 мм (см. рис. 33).
Элементы свода армируются двумя слоями тканой сетки № 10-1 по ГОСТ 3826-82* сварными плоскими каркасами из стальной низкоуглеродистой проволоки класса Вр-I с площадью сечения арматуры As = A's = 8×28,3 = 226 мм2.
Расчетное сопротивление и модули упругости арматуры для тканой сетки Rm = Rmc = 245 МПа, Em = 150000 МПа, для сварных каркасов Rs = Rsc = 355 МПа, Es = 200000 МПа. Расчетное сопротивление сжатию мелкозернистого бетона класса В40 группы А равно Rb = 22 МПа, модуль упругости бетона естественного твердения Eb = 28500 МПа. Расчетное сопротивление для предельных состояний второй группы Rbt, ser = 2,1 МПа.
В сечении свода изгибающий момент от продолжительно действующей нагрузки, равный Me = 146 кН×м, N = 300 кН и полный изгибающий момент M = 274 кН×м, N = 555 кН. Требуется рассчитать внецентренно сжатое сечение свода по ширине раскрытия трещин.
Расчет. Коэффициент сетчатого армирования полки (при коэффициенте армирования одной сетки на 1 см толщины μm = 0,0071) равен:
полки
μmc = μmt = 0,0071×2/3 = 0,0047;
стенки
μmω = 0,0071×2/2 = 0,0065.
Коэффициент приведенного по расчетным сопротивлениям арматуры армирования равен:
полки
μmc1 = 0,0047 + 0,0094×355/245 = 0,018,
где μs = μ's = As/Ab = 226/24000 = 0,0094;
стенки
μmω = 0,0065.
Приведенный коэффициент армирования с учетом модулей упругости
μmc(E) = μmt(E) = 0,0047 + 0,0034×200000/15000 = 0,017;
μmω(E)1 = μmω = 0,0065.
Поскольку сечение и его армирование симметричны, расстояние от центра массы до растянутой грани сечения yc = h/2 = 500 мм.
Статический момент площади таврового сечения (без свесов в растянутой зоне) относительно нижней грани
Sb = 800×30(1000 - 30/2)(1 + 5,26×0,017) + 940(940 + 30)(940 + 30)/2×(1 + 5,26×0,0065) = 71479746 мм3,
где α = Em/Eb = 150000/28500 = 5,26;
tω1 = tωn/sinβ = 22,4 : 0,94 = 94 мм при β = 70°.
Приведенная суммарная площадь Ab таврового сечения Ab = 800×30(1 + 5,26×0,017) + 94(940 + 30)(1 + 5,26×0,0065) = 120426 мм2. Приведенная площадь свесов растянутой полки Aft = (800 - 84)30(1 + 5,26×0,017) = 23074 мм2.
Полученные значения подставляем в формулу (78) и вычисляем высоту сжатой зоны:
h - x = Sb/(Ab + Aft/2) = 71479746 : (120426 + 23074 : 2) = 541,7 мм; x = h - 541,7 = 1000 - 542 = 458 мм.
Пластический момент сопротивления приведенного сечения по формуле (79)
Wpl = 0,292 + 0,75(0,2253 + 2×0,017×5,26) + 0,075(0,45 + 2,0×0,017×5,26)94×10002 = 60376670 мм3,
где γ1 = (bf - tω)tf/(tωh) = (800 - 94)30 : (94×1000) = 0,2253;
γ2 = 2(b'f - tω)/(tωh) = 2(800 - 94)30 : (94×1000) = 0,45.
Расстояние от центра тяжести сечения до ядровой точки
r = Wpl/Ab = 60376670 : 143673 = 420,2 мм,
где Ab = 800×30(1 + 5,26×0,017) + 94×940(1 + 5,26×0,0065) + 800×30(1 + 5,26×0,017) = 143673 мм2.
Приведенный модуль упругости арматуры по формуле (87)
Em1 = (Emμm + Esμs)/(μm + μs) = (150000×0,0047 + 200000×0,0094) : (0,0047 + 0,0094) = 183333 МПа.
Размеры сечения, приведенного к стальному, равны:
tsf = μmt(E)1tf = 0,017×30 = 0,51 мм;
tsω = μmω(E)tω = 0,0065×94 = 0,61 мм;
t'sf = μmc(E)1t'f + t'fEb/Em1 = 0,017×30 + 30×28500 : 183333 = 5,17 мм;
t'sω = μmω(E)tω + tωEb/Em1 = 0,0065×94×28500 : 183333 = 15,22 мм.
Координата центра тяжести приведенного стального сечения
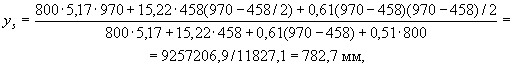
где расстояние между центрами сжатой и растянутой полок
h1 = h - (t'f + tf)/2 = 1000 - (30 + 30) : 2 = 970 мм.
Момент инерции сечения, приведенного к стальному, равен:
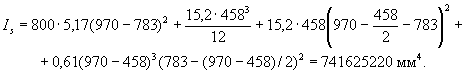
Момент сопротивления сечения, приведенного к стальному, равен:
Ws1 = Is/1,3ys = 741625220 : (1,3×782,7) = 782862,8 мм3.
Максимальные напряжения во внецентренно сжатом элементе:
σm = N(ec - r)/Ws1 = 555(490 - 420,2) : 728862,8 = 53,15 МПа;
ec = M/N = 274 : 555 = 0,49 м = 490 мм;
σm = N(ec - r)/Ws1 = 200(910 - 420,2) : 728862,8 = 134,4 МПа,
при эксцентриситете ec = M/N = 182/200 = 0,91 = 910 мм. Приведенный диаметр стержней и проволоки в полке по формуле (86)
ds = (n1d21 + … + nkd2k)/(n1d1 + ... + nkdk) = (160×12 + 8×82) : (160×1 + 8×8) = 3 мм.
Ширина раскрытия трещин acrc, нормальных к продольной оси элемента, при комбинированном армировании, равна (коэффициенты φ; φe; γm и ηm определяем по п. 4.9):
acrc = φφeγmηm(σm/Em1)20(3,5
- 100μmt1)![]() =
1×1,5×3×1×134,4 : 183333×20(3,5
- 100×0,017)
=
1×1,5×3×1×134,4 : 183333×20(3,5
- 100×0,017)![]() = 0,205 мм.
= 0,205 мм.
Ширина раскрытия трещин от кратковременного действия всей нагрузки
acrc1 = 1×1×3×1×53,15/183333×20(3,5
- 100×0,017)
![]() = 0,054 мм.
= 0,054 мм.
В соответствии с п. 4.12 ширина непродолжительного раскрытия трещин от действия полной нагрузки определяется как сумма ширины раскрытия трещин от продолжительного действия постоянных и длительных нагрузок и приращения раскрытия трещин от действия кратковременной нагрузки.
acrc = acrc1 - acrc2 + acrc3,
где acrc1 - ширина раскрытия трещин от непродолжительного действия всей (полной) нагрузки
acrc1 = 0,054 мм.
Напряжения для определения ширины раскрытия трещин при непродолжительном действии постоянных и длительных нагрузок
σm = N(ec - r)/Ws = 300(487 - 420,2) : 728862,8 = 27,6 МПа,
где ec = M/N = 146/300 = 0,487 м = 487 мм.
Начальная ширина раскрытия трещин от постоянных и длительных нагрузок при их непродолжительном действии
acrc2 = 1×1,3×1×27,6/183333
- 20(3,5 - 100×0,017)![]() = 0,012 мм.
= 0,012 мм.
Ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок acrc3 = acrc2×1,5 = 0,012×1,5 = 0,018 мм. Ширина раскрытия трещин acrc = 0,054 - 0,012 + 0,018 = 0,06 мм < 0,1 мм. Раскрытие трещин допустимое.
Пример 27.
Дано. Двутавровое приведенное сечение складчатой панели, которое имеет стенки и полки толщиной 20 мм и армируется двумя ткаными сетками № 10-1 - ГОСТ 3826-82*, выполнено из мелкозернистого бетона группы А класса В30 с прочностью на осевое сжатие Rb = 17 МПа. Модуль упругости при естественном твердении Eb = 26000 МПа. Коэффициент сетчатого армирования при одной сетке на 1 см толщины сечения составляет μm = 0,0071. Расчетное сопротивление и модуль упругости сетки равны:
Rm = Rmc = 245 МПа; Em = 150000 МПа.
Ширина сжатой полки b'f = 900 мм, толщина t'f = 20 мм, высота сечения h = 240 мм. Ширина растянутой полки bf = 1800 мм, толщина tf = 20 мм. Толщина вертикальной приведенной стенки сечения β = 75°
tω = tn/sinβ = 20×8 : 0,965 = 165,5 мм.
Требуется рассчитать армоцементную складчатую панель по ширине раскрытия трещин при действии изгибающего момента Mtot = 37,5 кН×м, продолжительно действующего момента Mp = 30,4 кН×м.
Расчет. Поскольку Me/Mtot = 3,04/3,75×3,04 = 0,81 > 2/3, проверяется продолжительное раскрытие трещин от действия момента Me.
Толщина сжатой полки в сечении, приведенном к стальному, равна:
t'sf = μmc(E)t'f + t'fEb/Em1 = 0,0071×20 + 20×26000 : 150000 = 3,48 мм.
Коэффициент армирования стенки и полок в сжатой и растянутой зоне равен:
μmc(E) = μmt(E) = μmω(E) = 0,0071.
Толщина растянутой полки приведенного стального сечения
tsf = μmt(E)tf = 0,0071×20 = 0,142 мм.
Толщина стенки в сжатой зоне, приведенная к стальному сечению,
tsωc = μmω(E)tω + tωEb/Em = 0,0071×165,5 + 165,5×26000 : 150000 = 29,865 мм.
Толщина стенки в растянутой зоне, приведенная к стальному сечению,
tsωt = μmω(E)tω = 0,0071×165,5 = 1,175 мм.
Статический момент площади относительно нижней грани
S1 = b'ft'f(1 + αμmc(E))(h - t'f/2) + tωhω(1 + αμmω(E))(h - t'f - hω/2) + bftf(1 + αμmt(E))tf/2 = 920×20(4×5,77×0,0071)(240 - 20 : 2) + 165,5×195(1 + 5,77×0,0071)(240 - 20 - 195 : 2) + 1800×20(1 + 5,77×0,0071)20 : 2 = 8895741,8 мм3.
Отношение модулей
α = Em/Eb = 15000 : 26000 = 5,77.
Площадь приведенного сечения
Ab = b'ftf(1 + αμmc(E)) + tωhω(1 + αμmω(E)) + bftf(1 + αμmt(E)α) = 920×20(1 + 5,77×0,0071) + 165,5×195(1 + 5,75×0,0071) + 1800×20(1 + 5,77×0,0071) = 90226,1 мм2.
Расстояние до центра тяжести
ycm = S1/Ab = 8895741,8 : 90226 = 98,59 мм.
Статический момент сечения, приведенного к стальному, относительно нижней грани сечения равен:
Ss1 = b'ft'sfy'1 + tsωchsωcy2 + bsωty3 + bsft2t/2 = 920×3,48×220 + 29,865×121,4×60,7 + 98,59×49,3 + 1800×0,1422 : 2 = 930155 мм3.
Площадь поперечного сечения, приведенного к стальному, равна:
As = b'ft'sf + tsωchsωc + bsωttsf + bsftf = 920×3,48 + 29,865×121,4 + 98,59×1,175 + 1800×0,142 = 7198,65 мм2.
Расстояние от центра тяжести до нижней грани
ys = Ss1/As = 930155,8 : 7198,65 = 129,21 мм.
Момент инерции, приведенный к стальному, относительно центра тяжести равен:
Is1 = b'f(t'sf)3/12 + b'ft'sf/(h - ys)2 + tsωch3sωc/12 + tsωchsωc[(h1 - ys)/2]2 + tsωth3sωt/12 + tsωthsωt (ys/2)2 + bft3sf/12 + bftsf(tsf/2)2 = 920×3,483 : 12 + 920×3,48×2202 + 29,86×90,83 : 12 + 29,86×90,8×64,62 + 1,175×1293 : 12 + 1,175×129×64,22 + 1800×0,1423 : 12 + 1800×0,142(0,142 : 2) = 27469958 мм4.
Момент сопротивления сечения, приведенного к стальному по формуле (91), равен:
Ws1 = Is1/1,3ys = 27469958 : (1,3×129,21) = 163538,41 мм3.
Напряжение в растянутой зоне приведенного сечения по формуле (89)
σm = M/Ws1 = 3040000 : 163538 = 18,6 МПа.
Ширина раскрытия трещин acrc, нормальных к оси элемента при сетчатом армировании по формуле (84), равна:
acrc = ηmφeσmSm/Em = 3,5×1,5×18,6 : (150000×10) = 0,065 мм.
Такая величина раскрытия трещин (табл. 1) допустима.
Пример 28.
Дано. Часть плиты, расположенная между ребрами, имеет толщину 20 мм и ширину 1 м. Пролет равен 1,2 м. Плита находится под воздействием длительно действующей части нагрузки - M1 = 20 кН×м и N = 36 кН, постоянно действующей нагрузки - M2 = 15 кН×м и N = 30 кН. От полной нагрузки M3 = 30 кН×м, N = 60 кН. Участок плиты армируется четырьмя слоями тканой сетки № 10-1 по ГОСТ 3826-82* (см. рис. 32).
Расчетное сопротивление и модули упругости арматуры и бетона равны Rm = Rmc = 245 МПа, E = 150000 МПа; для мелкозернистого бетона класса В35 группы А Rb = 19,5 МПа.
Начальный модуль упругости мелкозернистого бетона, не подвергнутого тепловой обработке по табл. 10, равен Eb = 27500 МПа.
Требуется рассчитать плиту покрытия в стадии эксплуатации по ширине раскрытия трещин.
Расчетная длина плиты (считая торцы плиты защемленными)
l0 = 0,5l = 0,5×120 = 60 см.
Эксцентриситеты сжимающей силы равны:
от длительно действующей части нагрузки
ec = M1/N1 = 20 : 36 = 0,55 м;
от постоянно действующей нагрузки
ec = M2/N2 = 15 : 30 = 0,5 м;
от всей нагрузки
ec = M3/N3 = 30 : 60 = 0,5 м.
Коэффициент армирования всего сечения сетками (при коэффициенте армирования μm = 0,0071 и одной сетки на 1 см толщины плиты) равен
μm1 = μmn/t = 0,0071×4 : 2 = 0,0142.
Момент инерции сечения относительно центра массы приведенного сечения
I1 = bt3/12 = 1000×203 : 12 = 666666,7 мм4.
Момент сопротивления сечения
W = I1/y = 666666,7 : 10 = 66666,67 мм3.
Величина момента сопротивления приведенного сечения для крайнего растянутого волокна
Wpl = γW = 1,75×66666,67 = 116666,6 мм3,
где γ определяется по табл. 13.
Для симметричного сечения (при симметричном армировании) высота сжатой зоны бетона в момент трещинообразования равна половине толщины плиты, т.е. x = t/2 = 10 мм.
Толщина сжатой зоны приведенного к стальному сечению
tsc = Amc/b + xEb/Em = 157 : 1000 + 10×27500 : 150000 = 1,99 мм.
Толщина растянутой зоны, приведена к стальному сечению,
tst = Amt/b = 157 : 1000 = 0,157 мм.
Положение центра тяжести приведенного стального сечения
ys1 = tscb(h1 - tsc/2)/[b(tst + tsc)] = 1,99×1000(16 - 1,99 : 2) : [1000(1,99 + 0,157)] = 13,91 мм.
Момент инерции сечения, приведенного к стальному (без учета, ввиду их малости, моментов инерции сжатой и растянутой зон этого сечения относительно собственных центров масс), равен:
Is = btsty2s1 + btsc(h1 - ys1 - tsc/2)2 = 1000×0,157×13,912 + 1000×1,99(15 - 13,91 - 1,99 : 2)2 = 30395,56 мм4.
Момент сопротивления сечения, приведенного к стальному, равен:
Ws = Is/ys = 30395,56 : 13,91 = 2185,16 мм3.
Расстояние от центра тяжести сечения до ядровой точки
r = Wpl/Ab = 116665,5 : 20000 = 5,83 мм.
Эксцентриситет продольной силы с учетом коэффициента η, учитывающего влияние прогиба,
ec = Mη/N = 360 : (60×1,58) = 7,9 мм.
Максимальное напряжение, возникающее в растянутой сетке от действия всей нагрузки по формуле (90), равно:
σm = 60000(7,9 - 5,83)/2185,10 = 56,84 МПа.
Ширина раскрытия трещин acrc при сетчатом армировании от непродолжительного действия всей нагрузки по формуле (84) равна:
acrc = ηmφeσmSm/Em = 3,5×1×56,84×10 : 150000 = 0,013 мм.
Напряжения σm от действия постоянных и длительных нагрузок, необходимые для определения ширины раскрытия трещин при их непродолжительном действии по формуле (90), равно:
σm = 66000(8,38 - 5,83)/2185,16 = 77 МПа.
Величины, необходимые для подстановки в формулу (90):
M = 20 + 15 = 35 кН×м; N = 36 + 30 = 66 кН.
Эксцентриситет
ec = Mη/N = 35 : (66×1,58) = 8,38 мм.
Ширина раскрытия трещин от постоянных и длительных нагрузок при их непродолжительном действии по формуле (84)
acrc2 = 3,5×1×77×10 : 150000 = 0,018 мм.
Ширина продолжительного раскрытия трещин по формуле (84)
acrc3 = 3,5×1,5×77×10 : 150000 = 0,027 мм.
Ширина непродолжительного раскрытия трещин от действия полной нагрузки определяется по формуле (92)
acrc = acrc1 - acrc2 + acrc3 = 0,013 - 0,018 + 0,027 = 0,022 мм;
acrc1 = 0,1 > acrc = 0,022.
Раскрытие трещин не превышает допустимое.
Пример 29.
Дано. Армоцементный складчатый элемент высотой h = 1000 мм, шириной верхней и нижней полки b'f = bf = 400 мм, толщиной полки t'f = tf = 30 мм, наклонных граней, с углом наклона к вертикали β = 60°, tω = 20 мм находится под действием поперечной силы (см. рис. 34) Q = 100 кН. Складчатый элемент армируется четырьмя ткаными сетками № 10-1 - ГОСТ 3826-82* в каждой наклонной грани в пределах действия среза.
Требуется рассчитать наклонное сечение элемента по раскрытию трещин.
Расчет выполняем в соответствии с п. 4.13. Коэффициент армирования наклонной грани элемента (при одной сетке на 1 см толщины μ = 0,0071)
μm1 = 0,0071×4 : 2 = 0,0142.
Высота наклонной стенки
hω = h - (t'f + tf) = 1000 - (30 + 30) = 940 мм.
Толщина (приведенная) стенки
tω1 = 2×20/sin 60° = 40 : 0,866 = 46,19 мм.
Коэффициент K2 по формуле (95)
K2 = Q/(tω1hω) - 0,25Np/Ab = 100000 : (46,2×940) = 2,302.
Коэффициент K1 для тканых сеток равен:
K1 = 102(30 - 1500μm1) = 102(30 - 1500×0,0142) = 870.
Коэффициент φe (п. 4.8) для продолжительной действующей нагрузки и мелкозернистого бетона группы А равен φe = 1,5.
Коэффициент ηm (п. 4.8) для тканых сеток равен: ηm = 3,5. Выполняем подстановку полученных величин в формулу (94). Ширина раскрытия трещин, наклонных к продольной оси изгибаемого элемента, равна:
acrc = φeK1(hω + 30dm)ηmK22/(μmω1E2m) = 1,5×870(940 + 30×1)35×2,3022 : (0,0142×1500002) = 0,15 мм.
Ширина раскрытия наклонной трещины от продолжительно действующей нагрузки acrc = 0,15 мм < acrc = 0,2 мм удовлетворяет требованиям.
Пример 30.
Дано. Складчатая панель высотой 1000 м, шириной 2000 мм и толщиной наклонных стенок tω = 20 мм армируется в каждой наклонной стенке четырьмя ткаными сетками № 8-0,7 по ГОСТ 3826-82* (см. рис. 34). В сечении действует от всей нагрузки поперечная сила Q = 140 кН от постоянно действующей нагрузки Q = 90 кН и от непродолжительно действующей нагрузки Q2 = 50 кН. Кроме того, в сечении действует продольная сила от преднапряженной арматуры Np = 200 кН. Складка изготовлена из мелкозернистого бетона класса В35. Модули упругости арматуры принимаются для тканой сетки Em = 150000 МПа.
Требуется рассчитать ширину раскрытия наклонных трещин. Расчет выполняем в соответствии с п. 4.13.
Коэффициент армирования наклонных граней равен:
μmω1 = μmω4/2 = 0,0044×4 : 2 = 0,0088.
Коэффициент K1 для тканых сеток:
K1 = 102(30 - 1500μm1) = 102(30 - 1500×0,0088×1,41) = 1170.
Принимаем ηm = 3,5; φe = 1 в соответствии с п. 4.8. Площадь поперечного сечения
Ab = b'ft'f + bftf + tωhω = 20×400 + 20×400 + 46,19×940 = 56000 мм2.
Коэффициент
K2 = Q/(tωhω) - 0,25Np/Ab = 140000 : (20,2×940) - 0,25×200000 : 56000 = 2,83.
Ширина раскрытия наклонных трещин
acrc
= 1×1170(940
+ 30×0,7)
![]() = 0,114 мм < 0,15 мм.
= 0,114 мм < 0,15 мм.
Ширина раскрытия наклонных трещин не превышает допустимых пределов.
РАСЧЕТ ЭЛЕМЕНТОВ АРМОЦЕМЕНТНЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ
4.14. Деформации (прогибы, углы поворота) элементов армоцементных конструкций вычисляются по правилам строительной механики в зависимости от значений кривизны, определенных согласно указаниям пп. 4.15 - 4.20.
Значения кривизны и деформаций армоцементных элементов отсчитываются от их начального состояния, при наличии предварительного напряжения арматуры - от состояния до обжатия элемента. Элементы или участки элементов рассматриваются без трещин в растянутой зоне; если трещины не образуются при действии постоянных, длительных и кратковременных нагрузок, нагрузки вводятся в расчет с коэффициентом надежности по нагрузке γf = 1.
При расчете по деформациям усилия от усадки бетона Nshr принимаются равными нулю.
4.15. Жесткость элементов при кратковременном действии нагрузки определяется по формуле
Bf1 = 0,85EbI1, (96)
где Eb - модуль упругости бетона, принимаемый по табл. 10; I1 - момент инерции армированного сечения, приведенного к бетонному, с учетом коэффициентов сетчатого армирования в соответствии с отношением модулей Es/Em.
Приведенные коэффициенты армирования для расчета деформаций определяются по формулам:
для сжатой полки
μ'm1(E) = μ'mf + μsEs/Em;
для стенки
μm1(E) = μmω;
для растянутой полки
μm1(E) = μmf + μsEs/Em. (97)
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ НА УЧАСТКАХ БЕЗ ТРЕЩИН В РАСТЯНУТОЙ ЗОНЕ
4.16. Полное увеличение кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов на участках, где не образуются нормальные или наклонные к продольной оси элемента трещины, должно определяться по формуле
ρtot = ρ1 + ρ2 - ρ3 - ρ4, (98)
где ρ1 и ρ2 - кривизны соответственно от кратковременных нагрузок (принимаемых согласно указаниям СНиП 2.03.01-84) и от постоянных и длительных нагрузок (без учета усилия P), определяемые по формулам:
здесь M - момент от соответствующей внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного сечения; Bf1 - жесткость сечения с учетом быстронатекающей ползучести определяется по формуле (96); φb2 - коэффициент, учитывающий влияние ползучести бетона и принимаемый равным: при влажности воздуха окружающей среды 40 % и выше - 2,6; для бетона, изготовленного с пропаркой - 3; при влажности воздуха окружающей среды ниже 40 % - 3,9; для бетона, изготовленного с пропаркой - 4,5; Bf2 - жесткость армоцементных конструкций при учете продолжительного действия нагрузки, принимаемая равной:
Bf2 = 0,85Bf1; (101)
ρ3 - кривизна, обусловленная выгибом элемента от непродолжительного действия усилия предварительного обжатия и определяемая по формуле
ρ3 = Plcp/Bf1; (102)
ρ4 - кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия и определяемая по формуле
ρ4 = (Σb - Σ'b)/h. (103)
Здесь Σb, Σ'b - относительные деформации бетона, вызванные его усадкой и ползучестью под действием усилия предварительного обжатия, определяемые соответственно на уровне растянутой и сжатой граней сечения по формулам:
Σb = σb/Em; (104)
Σ'b = σ'b/Em. (105)
Значение σb принимается численно равным сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона по указаниям СНиП 2.03.01-84 для арматуры растянутой зоны, а σ'b то же для напрягаемой арматуры, если бы она имелась на уровне крайнего сжатого волокна бетона.
Значения кривизны ρ3 и ρ4 для элементов без предварительного напряжения допускается принимать равными нулю.
4.17. При определении кривизны на участках с начальными трещинами в сжатой зоне бетона ρ1, ρ2, ρ3 должны быть увеличены на 15 %, а ρ4 - на 25 %.
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ НА УЧАСТКАХ С ТРЕЩИНАМИ В РАСТЯНУТОЙ ЗОНЕ
4.18. Полное значение кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов прямоугольного, таврового и двутавровых сечений на участке, где образуются нормальные к продольной оси элемента трещины, следует определять по формуле
ρtot = ρ5 - ρ6 + ρ7 - ρ4, (106)
где ρ5 - кривизна от непродолжительного действия всей нагрузки, на которую производится расчет по деформациям, согласно п. 4.22;. ρ6 - кривизна от непродолжительного действия постоянных и длительных нагрузок; ρ7 - кривизна от продолжительного действия постоянной и длительной нагрузок; ρ4 - кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия и определяемая по формуле (103).
4.19. Значение ρ5 определяется по формуле
ρ5 = Mcrc/Bf1 + (M - Mcrc)/Bf3, (107)
где M - момент от всей внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей черед центр тяжести приведенного сечения; Mcrc - момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин; Bf1 - определяется по формуле (96); Bf3 - определяется по формуле
Bf3 = kEbI1, (108)
здесь k - коэффициент, учитывающий снижение жесткости элемента, принимается по табл. 14.
Значение Mcrc определяется по формулам:
для элементов без предварительного напряжения арматуры
Mcrc = WplRbt, ser; (109)
для предварительно напряженных элементов
Mcrc = WplRbt, ser ± Mp, (110)
где Wpl - момент сопротивления для крайнего растянутого волокна сечения с учетом неупругих деформаций растянутого бетона, определяется по формулам (76) и (79).
Значение Mp в зависимости (110) определяется по формуле
Mp = P(lcp + r). (111)
Таблица 14
|
Коэффициент армирования, % |
Коэффициент h для элементов |
||
|
изгибаемых и растянутых |
внецентренно сжатых |
||
|
Сетчатое при сетках: |
|
|
|
|
тканых |
До 1,5 |
0,08 |
0,16 |
|
От 1,5 до 3 |
0,16 |
0,32 |
|
|
сварных |
До 1,5 |
0,1 |
0,2 |
|
От 1,5 до 3 |
0,2 |
0,4 |
|
|
Комбинированное при сетках: |
|
|
|
|
тканых |
До 1,5 |
0,08 |
0,16 |
|
сварных |
» 1,5 |
0,1 |
0,2 |
|
тканых |
От 1,5 до 3 |
0,1 |
0,22 |
|
сварных |
» 1,5 » 3 |
0,12 |
0,25 |
В формуле (110) знак «плюс» следует принимать, когда направления моментов Mcrc и Mp противоположны, знак «минус» - когда направления совпадают.
В формуле (111)
Mp - момент усилия Np относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещиностойкость которой нужно определить; значение Mp определяется по указаниям СНиП 2.03.01-84, принимая Wpl согласно п. 4.4.
4.20. Значение ρ6 определяется по формуле
ρ6 = Mser/Bf3. (112)
где Mser - момент от постоянных и длительных нагрузок относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного сечения; Bf3 - определяется по формуле (108).
4.21. Значение ρ7 определяется по формуле
где Mser - значение такое же, что и в формуле (112); B'f3 - определяется по формуле
B'f3 = 0,8Bf3, (114)
здесь Bf3 - принимается по формуле (108).
Таблица 15
|
№ п.п. |
Схема загружения |
Коэффициент m |
|
1 |
|
5/48 |
|
2 |
|
1/12 |
|
3 |
|
1/8 - x2/6 |
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
1/4 |
|
9 |
|
1/3 |
|
10 |
|
x(1/2 - x/6) |
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
4.22. Прогиб, обусловленный деформацией изгиба, определяется по формуле
![]() (116)
(116)
где Mx - изгибающий момент в сечении x от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении x по длине пролета, для которого определяется прогиб; ρtot, x - полная величина кривизны элемента в сечении x от нагрузки, при которой определяется прогиб; величина ρtot, x определяется по формулам (98), (106); знак кривизны ρ принимается в соответствии с эпюрой кривизны.
Для элементов постоянного сечения, имеющих трещины на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая кривизну для остальных сечений такого же участка изменяющейся пропорционально значениям изгибающего момента.
Для некоторых наиболее распространенных случаев загружения прогиб изгибаемого элемента постоянного сечения может определиться по формуле
f = mρtotl2, (117)
где m - коэффициент, принимаемый в зависимости от условий опирания и схем загружения (табл. 15); ρtot - кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб; l - расчетный пролет элемента.
ПРИМЕРЫ РАСЧЕТА
Пример 31.
Дано. Армоцементный складчатый элемент высотой 1000 мм, шириной 2000 мм, толщиной наклонных стенок tω = 20 мм, толщиной и шириной горизонтальных полок tf = t'f = 30 мм, bf = b'f = 200 мм армируется восемью сварными сетками № 12,5-0,5 - ТУ 14-4-713-76 в сжатой и растянутой полках сечения; четырьмя сварными сетками № 12,5-0,5 по ТУ 14-4-713-76 в наклонных гранях сечения; сварными плоскими каркасами из арматуры диаметром 10 мм класса А-III в сжатой и растянутой полках (A's = As = 78,5×4 = 314 мм2) (рис. 34).
Расчетные сопротивления и модули упругости арматуры и бетона равны: для сварных сеток Em = 150000 МПа, для арматуры класса А-III Es = 200000 МПа.
Для мелкозернистого бетона группы А класса В35 прочность на осевое сжатие, прочность на осевое растяжение Rbt, ser = 1,56 МПа, коэффициент условия работы γb1 = 1. Начальный модуль упругости бетона естественного твердения Eb = 27500 МПа.
В сечении действуют изгибающий момент от полной нагрузки Mtot = 200 кН×м и продольная сила Ntot = 800 кН, в том числе от части постоянных и длительных нагрузок Me = 170 кН×м, Ns = 690 кН.
Требуется определить прогиб складчатого элемента длиной 15 м.
Жесткость элемента при отсутствии трещин
Bf1 = 0,85×27500×10072,4×106 = 23543,3×1010 МПа.
Жесткость элемента при наличии трещин
Bf3 = KEbI1 = 0,25×27500×10072,4×106 = 69247,75×109 Н×мм2.
Значение k - коэффициента, учитывающего снижение жесткости элемента, принимаем по табл. 14.
Для элемента с комбинированным армированием при сварных сетках μm1 = 0,042, k = 0,25.
Приведенная площадь таврового сечения
A'b = 400×30(1 + 5,45×0,0384) + (940 + 30)46(1 + 5,45×0,0028) = 59812,3 мм2.
Приведенная площадь свесов растянутой полки
Aft = (400 - 46)30(1 + 5,26×0,0384) = 12776,2 мм2;
статический момент площади таврового сечения (без свесов растянутой полки) относительно нижней границы
Sb = 400×30(1000 - 30/2)(1 + 1,26×0,0384) + (940 + 30)46(940/2 + 30)(1 + 5,26) = 36599587 мм3.
Высота сжатой зоны h - x = 36599587/(59812,3 + 12776,2) = 552,86 мм, откуда x = 1000 - 552,86 = 447,14 мм.
Момент инерции сжатой зоны сечения относительно нейтральной оси
Ic1 = [400×303/2 + 400×30(447,14 - 30/2)2](1 + 5,26×0,0384) + [46(447,14 - 30)3/12 + 46(447,14 - 30)((447,14 - 30)/2)2] + 5,26×0,0028 = 94579730 + 1182481600 = 1277061330 мм4.
Статический момент растянутой части сечения относительно нейтральной оси
St = 400×30(1000 - 447,14 - 30/2)(1 + 5,26×0,0384) + [(940 + 30 - 447,14)46(940 + 30 - 447,14)/2](1 + 5,26×0,0088) = 14138332 мм3.
Момент сопротивления приведенного сечения по формуле (76)
Wpl = 2Ic1/(h - x) + St = 2×1277061,339 : (100 - 447,14) + 14138332 = 18758167 мм3.
Момент трещинообразования по формуле (109)
Mcrc = WplRbt, ser = 18758167×15,6 = 29,262 кН×м.
Складчатая плита работает с трещинами, так как Mcrc = 29,262 кН×м < M = 170 кН×м.
Кривизна от непродолжительного действия всей нагрузки по формуле (107)
ρ5 = Mcrc/Bf1 + (M - Mcrc)/Bf3 = 29,263×106 : (23543,3×106) + (200×106 - 29,263×106) : (6924,78×1010) = 0,025898×10-4 мм-1.
Кривизна от непродолжительного действия постоянных и длительных нагрузок ρ6 по формуле (112)
ρ6 = Me/Bf3 = 170×106 : (6924,78×1010) = 0,024549×10-4 мм-1.
Кривизна от продолжительного действия постоянной и длительно действующей нагрузок по формуле (113)
ρ7 = Me/B'f3 = 170×106 : (5539,82×1010) = 0,03069×10-4 мм-1,
где B = 0,8B = 0,8×6924,78×1010 = 5539,82×1010.
Суммарная кривизна в соответствии с п. 4.18 по формуле (106)
ρtot = 0,0258988×10-4 - 0,0245495×104 + 0,03069×10-4 = 0,0320393×10-4 мм-1.
Прогиб в середине элемента определяем по формуле (117):
f = mρtotl2 = (5 : 48)0,0320393×10-4×149002 = 7,4 мм.
Прогиб складки равен 74 мм. Допустимый прогиб 74,5 мм. Вычисленный прогиб меньше допустимого.
Пример 32.
Дано. Армоцементная складчатая плита покрытия с расчетным пролетом 5,95 м выполнена с армированием двумя ткаными сетками № 10-1 ГОСТ 3826-82* (коэффициент сетчатого армирования при одном слое сеток на 1 см толщины составляет μm = 0,0071) и сварными сетками из стальной низкоуглеродистой холоднотянутой проволоки класса Вр-I (в сжатой зоне восемь проволок диаметром 3 мм, A'm = 8×0,071 = 0,57 см2; в растянутой зоне 28 проволок диаметром 4 мм, Am = 28×0,126 = 3,53 см3) (см. рис. 38).
Плита выполнена из мелкозернистого бетона класса В40 группы А. Rbt, ser = 2,1 МПа, Eb = 28,5×103 МПа.
Изгибающий момент, действующий на плиту, равен: M = 30,446 кН×м.
Требуется произвести расчет по деформациям в случае отсутствия и в случае образования трещин в растянутой зоне.
Расчет по деформациям. Приведенная площадь двутаврового сечения
A1 = 92×2(1 + 5,26×0,0106) + 16,55×19,5(1 + 5,26×0,0071) + 184,0×2,5(1 + 5,26×0,0144) = 1023,88 см2,
где
α = Em/Eb = 150000 : 28500 = 5,26.
Приведенный статический момент площади двутаврового сечения относительно нижней грани
S1 = 92×2(1 + 5,26×0,0106)(24 - 2/2) + 19,5×16,55(1 + 5,26×0,0071)(24 - 2 - 19,5/2) + 184×2,5(1 + 5,26×0,0144)2,5/2 = 9187,52 см2.
Расстояние от центра тяжести сечения до нижней грани
yc = S1/A1 = 9187,52 : 1023,88 = 8,97 см.
Момент инерции относительно центра тяжести приведенного сечения
I1 = 92×23/12 + 92×2(24 - 8,97 - 2/2)2(1 + 5,26×0,0106) + 16,55×19,33/12(1 + 5,26×0,0071) + 184×2,53/12 + 184×2,5(8,97 - 2,5/2)2(1 + 5,26×0,144) = 81889,63 см4.
Приведенные коэффициенты армирования соответственно для стенки, сжатой и растянутой полок по формуле (97) равны:
μω(E)1 = μω = 0,0071;
μ'(E)1 = μ'm + μ'sEs/Em = 0,0071 + 0,0031×170000 : 150000 = 0,0106;
μ(E)1 = μm + μsEs/Em = 0,00567 + 0,00767×170000 : 150000 = 0,0144;
μm = 2μ/tf = 2×0,0071 : 2,5 = 0,00567;
μs = As/(bftf) = 3,53 : (184×2,5) = 0,00767.
Жесткость элементов до появления трещин при кратковременном действии нагрузки по формуле (96)
Bf1 = 0,85×81889,63×28500×100 = 1983776,1×105 Па×см2.
Жесткость элементов при наличии трещин и кратковременном действии нагрузки по формуле (107) равна: при коэффициенте K = 0,16 при μm1 = 1,8 % и тканых сеток по табл. 14.
Bf3 = 0,16×38500×81889,6×100 = 504440,1×105 Па×см2.
Так как по формуле (80) Wpl = γW1,
где
W1 = I1/yc; γ = 1,1 (см. табл. 13),
тогда Wpl = 1,1×81889,63/8,97 = 10042,206 см3.
Момент трещинообразования по формуле (109) и в соответствии с п. 4.14 равен:
Mcrc = 10042,206×2,1×100 = 2108863,26 Н×см.
Кривизна элемента при наличии трещин по формуле (107)
ρ5 = Mcrc/Bf1 + (M - Mcrc)/Bf3 = 2108863,26 : (1983776,13×105) + (3045000 - 2108863,26) : 50440,1208×105 = 2,918×10-5 см-1.
Момент от постоянных и длительных нагрузок Mser равен:
Mser = 19,82512 кН×м.
Кривизна ρ6 по формуле (112)
ρ6 = 1982512 : 504440,12×105 = 3,93×10-5 см-1.
Кривизна ρ7 по формуле (113)
ρ7 = Mser/B'f3; при B'f3 = 0,8 Bf3.
ρ7 = 1982512/0,8×504440,12×105 = 4,91×10-5 см-1.
Ссылаясь на п. 4.14, ρ4 принимаем равным нулю; тогда полная кривизна по формуле (106) равна:
ρtot = (2,92 - 3,93 + 4,9)10-5 = 3,9×10-5 см-1.
Прогиб панели по формуле (117) равен: m = 5/48 (см. табл. 15),
f = mρtotl2 = (5 : 48)3,9×5,952×10-5 = 1,4 см.
Поскольку 1,4 < 1/300×595 = 1,9 см, жесткость панели достаточна.
Пример 33.
Дано. Армоцементная складчатая плита покрытия, рассмотренная в прим. 1. Момент от нормативной нагрузки M = 87400 Н×м.
Требуется рассчитать плиту по деформациям.
Расчет. Момент при образовании трещин равен Mcrc = 62138 Н×м.
Жесткость сечения при кратковременном действии нагрузки по формуле (96) равна: Bf1 = 0,85×2,4×104×688085 = 14036×108 Па×см2.
Жесткость сечения с учетом коэффициента снижения жесткости k, принимаемого по табл. 14 и равного 0,08 по формуле (108), равна: Bf3 = 0,08×2,4×104×688085 = 1321×108 Па×см2.
Кривизна от непродолжительного действия всей нагрузки по формуле (107) равна:
ρ5 = 6213800/14036×108 + (8740000 - 6213800)/1321×108 = 2,363×10-5 см-1.
Кривизна от непродолжительного действия постоянных и длительных нагрузок по формуле (112) равна:
ρ6 = M/Bf3 = 6650000 : (1321×108) = 5,03×10-5 см-1.
Кривизна от продолжительного действия постоянных и длительных нагрузок по формуле (113) равна:
ρ7 = M/B'f3 = M/0,8Bf3 = 6650000 : (0,8×1321×108) = 6,29×10-5 см-1.
Полная кривизна по формуле (106) равна:
ρtot = ρ5 - ρ6 + ρ7 = (2,368 - 5,03 + 6,29)10-5 = 3,628×10-5 см-1.
Прогиб панели по формуле (117) равен:
f = mρtotl2 = (5 : 48)3,628×10-5×8952 = 3,03 см.
Так как f = 3,03 см < 1/250l = 1/250×895 = 3,58 см, следовательно, жесткость панели достаточна.
Пример 34.
Дано. Армоцементный элемент, приведенное двутавровое сечение которого имеет высоту 550 мм, толщину сжатой и растянутой полок 50 мм, толщину стенки 75 мм и ширину верхней полки 600 мм, а нижней - 500 мм, воспринимает действие продольной силы N = 155,11 кН от всей нагрузки и момент M = 52,136 кН×м; N1 = 127,16 кН и M1 = 20,34 кН×м от длительно действующей нагрузки.
Момент от полной нормальной силы N = 155,11 кН относительно центра тяжести арматуры растянутой полки
M = N(e0 + h/2 - tf/2) = 155110(40 + 55 : 2 - 5 : 2) = 100820 Н×м.
Момент, воспринимаемый нормальным сечением при образовании трещин, равен: Mcrc = 25,791 кН×м.
Момент от длительно действующей нормальной силы относительно центра тяжести арматуры растянутой полки
M = N(e0 + h/2 - tf/2) = 127160(16 + 55 : 2 - 5 : 2) = 52136 Н×м.
Требуется рассчитать армоцементный элемент по жесткости.
Расчет. Жесткость сечения при кратковременном действии всей нагрузки по формуле (96)
Bf1 = 0,85×23×104×521098 = 10185×108 Па×см2.
Жесткость сечения по формуле (108) с учетом коэффициента снижении жесткости k, принимаемого по табл. 14 и равного 0,16, равна:
Bf3 = 0,16×2,3×104×521098 = 1917×108 Па×см2.
Кривизна от непродолжительного действия всей нагрузки по формуле (107)
ρ5 = 2579100/(10185×108) + (1008200 - 2579100)/(1917×108) = 4,166×10-5 см-1.
Кривизна от непродолжительного действия постоянных и длительных нагрузок по формуле (112)
ρ6 = M/Bf3 = 5213600 : (1917×108) = 2,72×10-5 см-1.
Кривизна от непродолжительного действия постоянных и длительных нагрузок по формуле (113)
ρ7 = Mser/B'f3 = Mser/0,8Bf3 = 5213609 : (0,8×1917×108) = 3,4×10-5 см-1,
где B'f3 определяется по формуле (114).
Полная кривизна по формуле (106)
ρtot = ρ5 - ρ6 + ρ7 = (4,166 - 2,72 + 3,4)×10-5 = 4,846×10-5 см-1.
Прогиб панели по формуле (117)
f = mρtotl2 = (1 : 48)4,846×1×12002 = 1,45 см.
Так как f = 1,45 < 4,8 см, жесткость панели достаточна.
5. КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
ОБЩИЕ ПОЛОЖЕНИЯ
5.1. При проектировании армоцементных конструкций и изделий для обеспечения условий их экономичного и качественного изготовления, требуемой долговечности совместной работы арматуры и бетона надлежит выполнять конструктивные требования, изложенные в настоящем разделе.
5.2. Конструкции должны приниматься простого очертания, удобные для изготовления с максимальной степенью механизации, например плоские преднапряженные листы, изготовляемые на длинных стендах с последующим приданием этим листам цилиндрической формы, благодаря чему таким конструкциям присуща пространственная работа под нагрузкой. Следует использовать арматуру, закладные детали, выпускаемые в виде товарной продукции по нормалям и ГОСТам. Применяя арматуру для армирования плоских преднапряженных листов в виде товарных бухт высокопрочной проволоки и рулонов сетки, разматываемых на длинных стендах механически, будет достигнуто сокращение трудозатрат на изготовление армоцементных конструкций.
Распалубочную и отпускную прочность бетона следует назначать минимально возможными, а режимы термообработки ускоренными для увеличения оборота стенда и интенсивного использования производственных площадей.
Необходимо стремиться к унификации конструкции покрытий производственных зданий и крыш жилых домов, ограждающих конструкций элементов несъемной опалубки и др., выполнение которых возможно из плоских предварительно напряженных листов. Унификация конструкций необходима также из условия загрузки технологического оборудования, так как разовые конструкции не могут обеспечить загрузки технологического оборудования и вследствие этого создание высокомеханизированного производства таких конструкций не может быть экономически выгодным.
МИНИМАЛЬНЫЕ РАЗМЕРЫ СЕЧЕНИЙ ЭЛЕМЕНТОВ
5.3 (5.2). Минимальные размеры сечений элементов армоцементных конструкций, определяемые из расчета на действующие усилия по предельным состояниям первой и второй групп, должны назначаться с учетом требований к толщине защитного слоя бетона, расположения и анкеровки арматуры, унификации размеров сечений и армирования, а также технологии изготовления конструкций.
5.4. Толщину полок и стенок несущих армоцементных конструкций следует принимать не менее 15 и не более 30 мм. Контурные ребра, ребра жесткости, диафрагмы в случае, если эти элементы конструкции требуются по расчету, могут выполняться толщиной более 30 мм. Утолщения более 40 мм (контурные ребра, ребра жесткости, диафрагмы и т.п.) допускается выполнять без сеток с соблюдением правил конструирования железобетонных конструкций по СНиП 2.03.01-84.
В пределах участка конструкции, где отсутствует сетчатое армирование, требования в части толщины защитного слоя и ширины раскрытия трещин принимаются как для железобетонных конструкций.
5.5. Во избежание повреждений от местных концентраций напряжений при резком изменении направлений граней изделия, например во внутренних углах, рекомендуется предусматривать смягчение очертания в виде уклонов, фасок или закруглений, по возможности небольшой величины (до 30 мм), чтобы не требовалось местное армирование. Во внешних острых углах, во избежание откалывания бетона, следует устраивать скосы или закругления.
5.6. Отверстия в армоцементных элементах для пропуска коммуникаций, строповок и т.п. следует принимать по возможности небольшими и располагать их в пределах ячеек арматурных сеток и каркасов так, чтобы не нужно было перерезать основную арматуру и вводить дополнительное местное армирование. Углы отверстий желательно делать плавными.
5.7. При проектировании армоцементных конструкций их очертание следует принимать с учетом устройства и способа формования.
При применении неразъемных форм для возможности извлечения изделия из формы должны предусматриваться уклоны не менее 1:10. В случае применения неразъемных форм с использованием выпрессования уклон должен быть не менее 1:15.
При немедленной распалубке с обеспечением фиксированного вертикального перемешивания формующего элемента оснастки уклон должен быть не менее 1:50.
ЗАЩИТНЫЙ СЛОЙ БЕТОНА
5.8 (5.4). Защитный слон бетона, т.е. слой бетона от поверхности элемента до поверхности арматуры, должен быть достаточным для обеспечения совместной работы арматуры и бетона, защиты арматуры от коррозии на всех стадиях изготовления, монтажа и эксплуатации.
Проектная толщина защитного слоя бетона в армоцементных конструкциях должна быть не менее:
для сетки - 4 мм;
для стержневой и проволочной арматуры при наличии сеток в пределах защитного слоя бетона - 8 мм.
Толщину защитного слоя бетона следует принимать с учетом требований по технологии изготовления конструкций.
5.9. Для армоцементных конструкций без гидроизоляционного покрытия толщина защитного слоя бетона для напрягаемой арматуры в пределах длины зоны передачи напряжений lp должна приниматься не менее двух диаметров арматуры, но не более 15 мм.
5.10 (5.6). Во всех сборных изгибаемых элементах концы продольных стержней ненапрягаемой арматуры должны отстоять от торца элемента не более чем на 5 мм. Концы напрягаемой арматуры, а также анкеры необходимо защищать слоем мелкозернистого бетона не менее 5 мм.
5.11. При проектировании необходимо предусматривать меры по фиксации проектного положения сеток, стержневой и проволочной арматуры в сечении элемента (установкой прокладок и подкладок, шайб из бетона) применением машинной укладки сетки в процессе изготовления изделия поддержанием арматурного пакета в проектном положении перемещающимся ползунком впереди бетонирующего самоходного агрегата.
При невозможности выполнения этих требований должны применяться оцинкованные арматура и сетки.
АРМИРОВАНИЕ ЭЛЕМЕНТОВ
5.12. В элементах армоцементных конструкций сетки следует располагать на минимальном (в соответствии с п. 5.8) расстоянии от поверхности элементов для восприятия температурно-усадочных напряжений. Для восприятия растяжения, возникающего в зоне самозаанкеривания стержневой и проволочной арматуры, частые сетки рекомендуется располагать на минимальном расстоянии от поверхности этой арматуры.
5.13. В пределах полки или стенки элементов армоцементных конструкций должно располагаться симметрично относительно срединной поверхности не менее двух сеток.
Изгибаемые элементы прямоугольного сечения допускается армировать в растянутой зоне одной или несколькими сетками. Армоцементные элементы с конструктивным армированием допускается армировать одной сеткой, расположенной в их срединной поверхности.
Армоцементные элементы армировать в количестве более четырех сеток на 1 см толщины не допускается.
5.14. Отдельные стержни ненапрягаемой или напрягаемой арматуры в стенках и полках элементов армоцементных конструкций должны располагаться, как правило, равномерно по сечению, предусматривая установку большого количества стержней меньшего диаметра при минимальном расстоянии между ними.
Арматуру следует предусматривать так, чтобы при том же расходе металла количество классов и диаметров арматуры было минимально. Арматура должна допускать укладку ее в форму в соответствии с принятой технологией: готовыми пакетами до укладки бетона; готовыми пакетами в свежеуложенный бетон; отдельными сетками в свежеуложенный бетон; отдельными сетками в процессе укладки бетона.
5.15 (5.11). Отверстия в армоцементных конструкциях следует окаймлять дополнительной арматурой, сечение которой должно быть не менее сечения рабочей арматуры, расположенной в пределах отверстия, требуемой по расчету плиты как сплошной. При конструктивном армировании плиты и небольших размерах отверстий край плиты армируется исходя из конструктивных требований.
При наличии сосредоточенных нагрузок по краям плиты армирование и утолщение должны выполняться по расчету.
5.16 (5.12). Арматурные сетки в армоцементных конструкциях должны быть заведены за линию пересечения срединных плоскостей стенки и полки на длину не менее утроенной ширины ячейки сетки и не менее 30 мм.
ОСОБЕННОСТИ АРМИРОВАНИЯ ВНЕЦЕНТРЕННО СЖАТЫХ ЭЛЕМЕНТОВ
5.17 (5.13). Коэффициент сетчатого армирования внецентренно сжатых элементов в направлении действия усилия сжатия должен, как правило, составлять не более 1,5 %.
5.18 (5.14). Стержневую и проволочную арматуру во внецентренно сжатых элементах следует предусматривать диаметром не более 1/2 толщины полки или стенки и не более 8 мм.
В перегибе сеток рекомендуется устанавливать стержни.
5.19. Сетки в сжатых элементах должны располагаться в крайнем возможном положении относительно центра тяжести сечения, чтобы повысить жесткость элемента против выпучивания.
ОСОБЕННОСТИ АРМИРОВАНИЯ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ
5.20 (5.16). В изгибаемых элементах таврового, двутаврового сечений (или приводимого к ним сечения) с полкой в растянутой зоне продольная стержневая или проволочная арматура должна располагаться в растянутой зоне сечения симметрично относительно вертикальной оси элемента.
5.21 (5.17). Поперечное армирование элементов, как правило, выполняется сетками с квадратной ячейкой.
5.22. Анкеровка поперечной арматуры в полках изгибаемых элементов должна выполняться согласно требованиям п. 5.16 настоящих норм.
5.23 (5.19). Армирование цилиндрических, складчатых и коробчатых элементов следует предусматривать неразрезными сетками с их перегибом по линии примыкания граней.
5.24 (5.20). Диаметр стержневой и проволочной арматуры изгибаемых элементов должен предусматриваться с учетом возможности расположения арматуры в тонкостенном сечении или в утолщениях.
Стержневую и проволочную арматуру диаметром 8 мм и более, а также канаты диаметром более 6 мм допускается предусматривать только в ребрах элемента.
МИНИМАЛЬНОЕ РАССТОЯНИЕ МЕЖДУ СТЕРЖНЯМИ АРМАТУРЫ
5.25 (5.21). Расстояние между напрягаемой арматурой должно быть не менее 3ds, где ds - диаметр стержня (каната).
5.26 (5.22). Расстояние между отдельными стержнями арматурных сеток, выполняющих также роль фиксатора проектного положения сетчатого армирования, следует назначать не более 15 см.
АНКЕРОВКА НЕНАПРЯГАЕМОЙ АРМАТУРЫ
5.27. Армоцементные конструкции должны проектироваться с арматурой, имеющей сцепление с бетоном по всей длине элемента. В случае необходимости, например для сокращения зоны анкеровки, допускается устройство анкеров. Применение конструкций, в которых арматура не имеет сцепления с бетоном, допускается при обосновании в установленном порядке.
5.28. На свободных опорах плоских изгибаемых элементов для обеспечения анкеровки сеток, доходящих до опоры, должны выполняться следующие требования (рис. 39):
длина опорного участка плиты lsup должна быть не менее 3t и не менее 40 мм;
длина запуска арматуры за грань опоры lsup,s должна быть не менее 20dm для сварных сеток и 30dm для тканых сеток, при комбинированном армировании 15ds, для плетеных сеток 50dm.
Участки сетки, заходящей за грань свободной опоры, должны иметь не менее двух поперечных анкерующих стержней.
5.29. Продольные стержни растянутой и сжатой арматуры должны быть заведены за нормальное к оси элемента сечение, в котором эти стержни учитываются с полным расчетным сопротивлением, на длину не менее lp, определяемую в соответствии с п. 2.26.
5.30. При невозможности выполнения требования п. 5.29 настоящего Пособия необходимо предусмотреть меры по анкеровке продольных стержней для обеспечения их работы с полным расчетным сопротивлением в рассматриваемом сечении:
Рис. 39. Схема свободного опирания армоцементных плоских изгибаемых элементов
Рис. 40. Приварка к концам стержней анкерующих пластин или закладных деталей
1 - пластина (рифленная в местах контактной сварки); 2 - рабочие стержни ненапрягаемой арматуры; 3 - место точечной электросварки; 4 - сетки
а) приварка к концам стержней анкерующих пластин или закладных деталей (рис. 40);
б) отгиб анкерных стержней по дуге окружности диаметром 10d, при этом длина прямого участка у начала зоны анкеровки должна быть не менее 5d, а на отогнутом участке стержня должна быть уложена дополнительная сетка.
5.31 (5.27). Продольные растянутые сетки должны быть заведены за нормальное к оси элемента сечение, в котором они необходимы по расчету, на длину не менее 20dm для сварных сеток и не менее 30dm для тканых сеток.
СТЫКИ СЕТЧАТОЙ И СТЕРЖНЕВОЙ АРМАТУРЫ
5.32 (5.28). Стыки сеток допускается осуществлять внахлестку, причем стыки в растянутой зоне изгибаемых или внецентренно сжатых элементов рекомендуется располагать в местах неполного использования сечения арматуры.
5.33. Стыки растянутых сеток в рабочем направлении, выполняемые внахлестку, должны иметь длину перепуска (нахлестки) в тканых сетках не менее 100 мм, в сварных - не менее 60 мм, а стыки не растянутых сеток - соответственно 50 и 30 мм (рис. 41). Стыки растянутых сеток элемента должны располагаться вразбежку. Сечение стыкованных сеток в одном месте или по длине нахлестки должно составлять не более 50 % общего сечения растянутых сеток.
В местах соединения сеток в рабочем направлении в каждой из стыкуемых сеток по длине нахлестки должно располагаться: для сварных сеток - не менее четырех поперечных проволок, приваренных ко всем продольным стержням сетки, а для тканых сеток - не менее шести поперечных проволок.
Рис. 41. Стыки сеток, выполняемые внахлестку
а - стыки растянутых тканых сеток в рабочем направлении; б - то же, конструктивные стыки; в - стыки растянутых сварных сеток в рабочем направлении; г - то же, конструктивные стыки
5.34 (5.30). Стыкование внахлестку стержневой и проволочной арматуры, которая используется с полным расчетным сопротивлением, в тонкостенных армоцементных элементах не допускается.
5.35 (5.31). Во внецентренно сжатых элементах сетки рекомендуется соединять в поперечном направлении между собой скрутками, сжимами или другими способами.
ЗАКЛАДНЫЕ ДЕТАЛИ
5.36. Закладные детали следует изготовлять из рифленых штампованных пластин толщиной не менее 5 мм с приваркой их контактной электросваркой к арматурным изделиям, а также анкерным стержням диаметром 3 - 6 мм (рис. 40).
5.37 (5.33). Стальные закладные детали должны быть защищены от коррозии в соответствии с требованиями СНиП 2.03.01-84.
СТЫКИ СБОРНЫХ ЭЛЕМЕНТОВ
5.38. Конструкция стыков сборных элементов, работающих на изгиб, внецентренное сжатие или растяжение, должна обеспечивать восприятие расчетных усилий с учетом возможных монтажных эксцентриситетов.
В случаях когда передача усилий в стыках осуществляется через закладные детали, анкерные стержни закладных деталей должны быть равнопрочными с прерываемой в стыке стержневой и проволочной арматурой и сетками соединяемых элементов.
Стыки сборных элементов рекомендуется предусматривать одним из следующих способов:
а) установкой диафрагм между торцами элементов и сваркой стальных закладных деталей накладными пластинками, пропускаемыми через отверстия в диафрагмах, с последующим замоноличиванием стыка;
б) устройством контурных ребер, контактной сваркой выпусков стержневой и проволочной арматуры и дуговой сваркой закладных деталей, стыкуемых элементов и ребер (рис. 42) с последующим замоноличиванием стыка;
в) соединением элементов с помощью предварительно напряженных стержней (рис. 42) с замоноличиванием шва для предварительно напряженных конструкций, а также стыкуемых насухо или с промазкой торцов стыкуемых элементов эпоксидным компаундом;
г) применением сквозной стержневой и проволочной арматуры, в том числе напрягаемой, в сборномонолитных конструкциях.
Рис. 42. Стыки складчатых сборных армоцементных конструкций, работающих на внецентренное сжатие и поперечную силу
а - стык, выполняемый с контурной диафрагмой, сваркой стальных деталей и выпусков арматуры с последующим замоноличиванием; б - стык, выполняемый с натяжением арматуры: 1 - складчатый элемент; 2 - диафрагма; 3 - стальные накладные пластины; 4 - закладные детали; 5 - контурная диафрагма; 6 - выпуски арматуры; 7 - бетон замоноличивания; 8 - стыковая напрягаемая арматура; 9 - продольная напрягаемая арматура; 10 - сварной шов; 11 - анкер на стыковом стержне; 12 - анкерная колодка
5.39 (5.35). Замоноличивание стыков сборных элементов следует, выполнять, как правило, путем заполнения шва между элементами мелкозернистым бетоном, причем ширина шва должна быть не более 1,5t и не менее 0,5 см. Допускается применение полимербетонов для замоноличивания швов шириной менее 1 см.
ДОПОЛНИТЕЛЬНЫЕ УКАЗАНИЯ ПО КОНСТРУИРОВАНИЮ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫХ ЭЛЕМЕНТОВ
5.40 (5.36). В предварительно напряженных элементах сетчатое армирование в пределах обжатой зоны должно быть минимальным, но не менее двух сеток. Сетки должны располагаться симметрично относительно напрягаемой арматуры.
5.41. У конца предварительно напряженных элементов в пределах зоны анкеровки напрягаемой арматуры на участке длиной не менее 50ds (где ds - наибольший диаметр напрягаемой арматуры) вне зависимости от способа анкеровки следует устанавливать не менее двух дополнительных сеток симметрично относительно этой арматуры (см. п. 5.12).
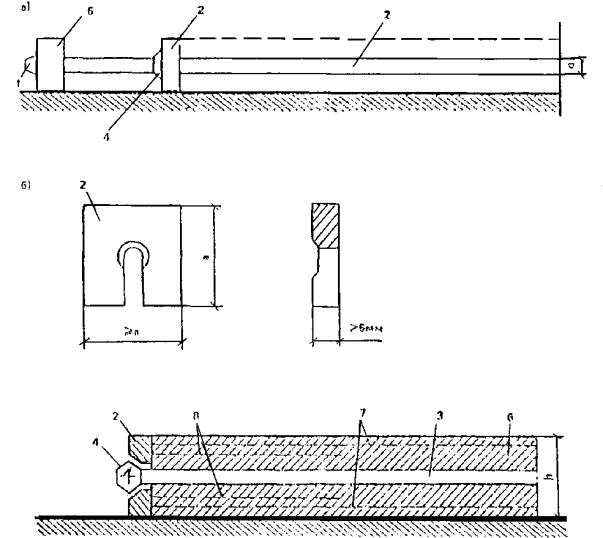
Рис. 43. Схема анкеровки напрягаемой арматуры
а - напрягаемая арматура, заанкеренная на упорах формы; б - элемент после отпуска предварительного напряжения арматуры; 1 - высаженная головка на конце проволоки; 2 - анкерная шайба с прорезью; 3 - проволока; 4 - промежуточная высаженная головка; 5 - неподвижный анкерный упор; 6 - предварительно напряженный элемент; 7 - основные сетки; 8 - дополнительные сетки
5.42. Анкеровка напрягаемой арматуры должна осуществляться с помощью специальных анкерных шайб и высаженных головок стержневой и проволочной арматуры (рис. 13). Допускается не применять анкерные устройства на концах напрягаемых стержневой и проволочной арматуры периодического профиля, если класс бетона и передаточная прочность бетона более значений, установленных в табл. 8 СНиП 2.03.03-85 и толщина защитного слоя бетона напрягаемой арматуры соответствует требованиям п. 5.8 - 5.9 настоящего Пособия.
ТРЕБОВАНИЯ, УКАЗЫВАЕМЫЕ НА РАБОЧИХ ЧЕРТЕЖАХ АРМОЦЕМЕНТНЫХ КОНСТРУКЦИЙ
Общие требования
5.43. В рабочих чертежах армоцементных конструкций или в пояснительной записке к ним должны быть указаны следующие требования:
а) класс бетона по прочности на сжатие и в случаях, предусмотренных в п. 2.6 марки бетона по морозостойкости и водонепроницаемости;
б) вид арматуры (сетка стержневая и проволочная) и ее профиль, класс арматуры, а в необходимых случаях (например, для конструкций, работающих при низких температурах) и марки стали, номер ГОСТа, а при его отсутствии номер технических условий на данный вид арматуры, методы изготовления арматурного каркаса, порядок его сборки, расход материалов;
в) мероприятия по антикоррозионной защите;
г) толщина защитного слоя бетона для рабочей арматуры, а также необходимость применения соответствующих методов фиксации, обеспечивающей проектное положение арматуры;
д) расчетные схемы, нагрузки, расчетные усилия в основных сечениях, в том числе от постоянных и длительных нагрузок.
Дополнительные требования, указываемые на рабочих чертежах элементов сборных армоцементных изделий.
5.44. В рабочих чертежах элементов сборных конструкций или в пояснительной записке к ним кроме данных, перечисленных в п. 5.43, должны быть указаны:
а) наименьшие размеры опорных участков;
б) степень (качество) отделки поверхности (при необходимости);
в) места для захвата при снятии с форм, подъеме и монтаже, место их опирания при транспортировании и складировании;
г) требования о нанесении заводом-изготовителем меток (рисок) для обеспечения качественной укрупнительной сборки, а для элементов с трудноразличимым верхом или торцами требование о нанесении заводом-изготовителем маркировки (надписи), обеспечивающей правильность положения таких элементов при их подъеме, транспортировании и укладке;
д) для элементов, образцы которых согласно требованиям нормативных документов испытываются загружением, должны указываться схемы испытания, величины нагрузок, прогибов и других контролируемых величин;
е) величина отпускной прочности бетона для предусмотренных условий монтажа и загружения;
ж) масса сборного элемента.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ РАБОЧИХ ЧЕРТЕЖЕЙ
5.45. Система оформления рабочих чертежей армоцементных конструкций должна обеспечивать удобство пользования чертежами на каждом технологическом переделе производства как в случае возведения монолитных армоцементных конструкций, так и в случае заводского изготовления и монтажа армоцементных изделий.
Рабочие чертежи следует оформлять на определенных исполнителей и службы. Должна быть обеспечена возможность передачи отдельных листов рабочих чертежей на технологические переделки без доработки, перечерчивания или составления дополнительных эскизов.
5.46. Рабочие чертежи армоцементных конструкций должны быть удобны для пользования. Рекомендуется оформление их в виде альбомов небольшого размера.
Целесообразно разделение альбомов рабочих чертежей на две части: 1 - общие виды конструкции, узлы, монтажные схемы армирования; 2 - рабочие чертежи арматурных элементов и закладных деталей.
Рабочие чертежи сложных арматурных изделий рекомендуется оформлять в виде ряда деталировочных чертежей, каждый из которых предназначен для выполнения определенных операций.
5.47. В рабочих чертежах армоцементных изделий массового производства рекомендуется предусматривать варианты отдельных конструктивных решений, учитывающих различные особенности технологии, в частности конструктивные решения арматурных элементов и закладных деталей. Должны быть даны указания, позволяющие производить замену отсутствующих видов арматуры, употребляемой в проекте без существенного ее перерасхода
ПРИЛОЖЕНИЕ 1
Рекомендуемый сортамент тканых и сварных проволочных сеток для армоцементных конструкций
|
№ сетки |
Номинальный диаметр проволоки сеток, мм |
Размер ячейки в свету, мм |
Площадь сечения одной проволоки, см2 |
Количество проволок на 1 м ширины сетки, шт. |
Масса 1 м2 сетки, кг |
Коэффициент сетчатого армирования при одном слое на 1 см толщины сечения элемента |
|
|
Тканые сетки по ГОСТ 3826-82 * |
6 |
0,7 |
6 ´ 6 |
0,00385 |
149 |
0,9 |
0,0058 |
|
7 |
0,7 1,1 |
7 ´ 7 7 ´ 7 |
0,00385 0,00951 |
130 124 |
0,8 1,9 |
0,005 0,0119 |
|
|
8 |
0,7 1,2 |
8 ´ 8 8 ´ 8 |
0,00385 0,01131 |
115 109 |
0,7 2,1 |
0,0044 0,0123 |
|
|
9 |
1 |
9 ´ 9 |
0,0785 |
100 |
1,3 |
0,0078 |
|
|
10 |
1 |
10 ´ 10 |
0,00785 |
91 |
1,2 |
0,0071 |
|
|
12 |
1,2 |
12 ´ 12 |
0,01131 |
76 |
1,4 |
0,0086 |
ПРИЛОЖЕНИЕ 2
Пример расчета армоцементной предварительно напряженной складки
Дано. Армоцементная предварительно напряженная складка имеет следующие размеры сечения: ширина 2 м, высота 1,2 м (рисунок). Пролет складки 18 м. Эксплуатируют конструкцию в отапливаемом помещении с относительной влажностью выше 40 %. Конструкция отвечает требованиям и категории трещиностойкости. На 1 м складки шириной 2 м действуют следующие нагрузки в кН×м:
нормативные:
постоянная gn = 2,3×2 = 4,6 кН×м;
временная (кратковременная) Pn = 1×2 = 2 кН×м;
полная, qn = gn + Pn = 4,6 + 2 = 6,6 кН×м;
расчетные:
постоянная g = 2,65×2 = 5,3 кН×м;
временная P = 1,4×2 = 2,8 кН×м;
полная q = 5,3 + 2,8 = 8,1 кН×м.
Расчетная схема для расчета складки принимается как для балки на двух опорах, загруженной равномерно распределенной нагрузкой.
1. Расчетный изгибающий момент в середине пролета от полной нагрузки
M = ql2/8 = 8,1×182 : 8 = 328 кН×м.
2. Изгибающий момент от полной нормативной нагрузки (для расчета прогибов и трещиностойкости)
Mn = qnl2/8 = 6,6×182 : 8 = 267,3 кН×м.
3. Изгибающий момент от нормативной постоянно действующей нагрузки Mng = 4,6×182/8 = 186,3 кН×м.
4. Момент от собственной массы конструкции Mcbn = 2,7×182/8 = 109 кН×м.
5. Момент от нормативной постоянной и длительной (30 % снеговой) нагрузки
Mn = (4,6 + 0,3)2×182/2 = 210,6 кН×м.
6. Момент от нормативной кратковременной нагрузки Mn = 2×182/8 = 81 кН×м.
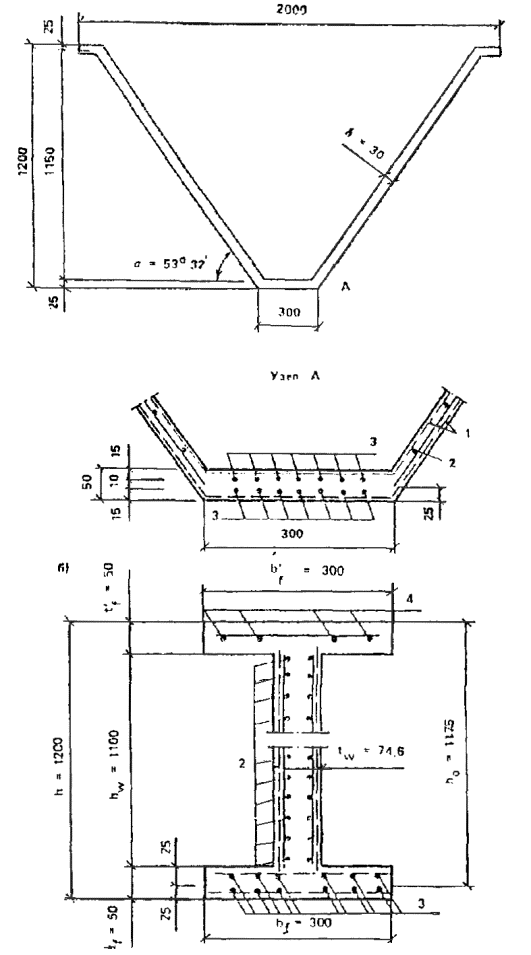
Рис. 44. Сечение армоцементной складки покрытия пролетом 18 м с предварительно напряженной арматурой
а - поперечное сечение складки; б - расчетное сечение; 1 - тканая сетка № 10-1 по ГОСТ 3826-82*; 2 - сварная сетка из проволоки Æ 5 Вр-I; 3 - напрягаемая арматура Æ 6 Вр-II
7. Максимальная поперечная сила на опоре от расчетной нагрузки
Q = ql/2 = 8,1×18 : 2 = 72,1 кН.
8. То же от нормативной нагрузки Qn = 6,6×18/2 = 59,4 кН.
Расчетные данные для подбора сечения
Принимаем, что складка изготовлена из тяжелого мелкозернистого бетона по прочности на сжатие класса В40 группы А, подвергнутого тепловой обработке. Марка по морозостойкости F100.
Прочностные характеристики бетона: модуль упругости Eb = 24500 МПа; Rb = 20 МПа; Rbt = 1,25 МПа для предельных состояний первой группы при γb2 = 0,9 (см. табл. 7); Rb, ser = 29 МПа; Rbt, ser = 2,1 МПа для расчетных предельных состояний второй группы (см. табл. 6).
Для напрягаемой арматуры 12 Æ 6 Вр-II, расположенной в нижней полке: Rs = 980 МПа для предельных состояний первой группы; Rs, ser = 1175 МПа для предельных состояний второй группы.
Площадь напрягаемой арматуры 12 Æ 6 Вр-II Ap = 340 мм2.
Для арматуры из сварных сеток в стенках из проволоки Æ 3 Вр-I по ГОСТ 6727-80* As = 71 мм2, Rs = 375 МПа, Rsω = 270 МПа, Es = 170000 МПа.
Для тканых сеток № 10-1 по ГОСТ 3826-82* (табл. 11) Rm = 245 МПа, Em = 150000 МПа, Rmω = 206 МПа.
Нижняя растянутая полка армируется предварительно напряженными стержнями 12 Æ 6 Вр-II (As = 340 мм2) и двумя ткаными сетками № 10-1.
Стенки армируются одним слоем сетки из проволоки Æ 3 Вр-I с шагом 100 мм, Asω = 71 мм2 и двумя слоями тканой сетки № 10-1.
Верхняя полка содержит один слой сетки из проволоки Æ 3 Вр-I с шагом 100 мм, A's = 28 мм2 в два слоя тканой сетки № 10-1.
Расчет по предельным состояниям первой группы
Расчет по прочности сечений, нормальных к продольной оси элемента. Для расчета приводим сечение элемента к двутавровому. Приведенная толщина стенки двутаврового сечения
tω1 = tωn/sinβ = 30 : (0,8042×2) = 74,6 мм,
где tω - толщина стенки, мм; n - число наклонных стенок; β - угол наклона стенки к горизонтали, град.
Коэффициент армирования верхней сжатой полки:
сварной сеткой из 4 проволок Æ 3 Вр-I A's = 28 мм2:
μs = A's/(b'ft'f) = 28 : (300×50) = 0,0019;
двумя слоями тканой сетки № 10-1
μ'm = 2A'm/t'f = 2×0,071 : 50 = 0,00284;
стенки толщиной 30 мм - двумя слоями тканой сетки № 10-1:
μmω = 2Aω/tω = 2×0,071 : 30 = 0,0047;
сеткой из проволоки Æ 3 Вр-I с шагом 100 мм Asω = 71 мм2:
μsω = Asω/(tωhω) = 71 : (30×1000) = 0,00284;
нижней растянутой полки - двумя слоями тканой сетки № 10-1:
μmf = 2Am/tf = 2×0,071 : 50 = 0,00284;
предварительно напряженной арматурой
μsf = As/(bftf) = 340 : (300×50) = 0,0227.
Приведенные коэффициенты армирования:
сжатой верхней полки
μ'mf = μ'm + μsRs/Rm = 0,0029 + 0,0019×375 : 245 = 0,0057;
стенки
μmωt = μsωRs/Rm + μmω = 0,0047 + 0,0024×375 : 245 = 0,0084;
нижней растянутой полки
μmf1 = μmf + μsfRs/Rm = 0,00284 + 0,0227×980 : 245 = 0,0936.
Расчет по прочности сечений, нормальных к оси элемента
Граничное значение относительной высоты сжатой зоны бетона ξ = x/h определяется из условия равновесия и граничного значения относительной высоты сжатой зоны, определяемого по формуле (8):
ξn = ω/[1 + σs(1 - ω/1,1)/σsc, u] = 0,54 : [1 + 790,6(1 - 0,54 : 1,1) : 500] = 0,306,
где ω - характеристика сжатой зоны бетона для армоцементных конструкций группы А определяется по формуле (9)
Rb = 20 МПа; ω = 0,7 - 0,008Rb = 0,7 - 0,008×20 = 0,54;
σs - напряжение в предварительно напряженной арматуре Вр-II с учетом первых и вторых потерь. σs = σsp2 = 790,6 МПа.
σsc, u = 500 МПа в соответствии с п. 3.12 СНиП 2.03.01-84.
Находим границу сжатой зоны бетона для двутаврового сечения из условия (15):
Rc1Afc > Rmμmf1Af + Rmμmω1Aωt,
где
Rcf1 = Rb + Rmcμmf1;
Acf = b'ft'f; Acω = (x - t'f)tω;
Aft = bftf; Aωt = (h - x - tf)tω;
Aω = hωtω; Rcω1 = Rb + Rmcμmω1.
После подстановки полученных величин в формулу (15) получаем, (20 + 245×0,0057)300×50 < 245×0,0936×300×50 + 245×0,0084×1100×74,6, 320,9 кН < 512,8 кН. Это значит, что граница сжатой зоны находится в ребре. В этом случае высота сжатой зоны бетона x находится из условия (18)
Rcf1Afc + Rcω1Acω = Rmμmf1At + Rmμmω1Amωt.
После подстановки значение x равно:
(20 + 0,0057×245)300×50 + (20 + 245×0,0084)(x - 50)74,6 = 245×0,0936×300×50 + 245×0,0084(1200 - x - 50)74,6; x = 157 мм.
Определяем условие ξ = x/h = 157/1200 = 0,131 < ξR = 0,306.
Находим по формуле (21) сумму моментов внутренних сил вычисленных относительно центра тяжести растянутой полки:
M = (20 + 245×0,0057)300×50[1200 - (50 + 50)/2] + (20 + 245×0,0084)(157 - 50)74,6[1200 - (157 - 50)/2] - 245×0,0084(1200 - 157 - 50)50 = 552×104 = 552 кН×м.
Так как 552 кН×м > 320,9 кН×м, следовательно, прочность нормального сечения обеспечена.
Расчет по прочности сечений, наклонных к продольной оси элементов
Проверяем условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами по формуле (57):
Q < 0,3φω1φb1Rbbhω1,
где φω1 = 1 + 5Em/Ebμmω1 = 1 + 5×150000/245000×0,0084 = 1,025;
γb = 1 - 0,01Rb = 1 - 0,01×20 = 0,8.
После подстановки получаем: Q = 72,1 кН < 0,3×1,025×20×74,6×1100 = 505000 Н.
Следовательно, прочность по сжатому бетону между наклонными трещинами обеспечена.
Расчет по прочности на поперечную силу выполняем по условию (60):
Q ≤ Qm + Qb,
где Q - поперечная сила, определяемая внешней нагрузкой по одну сторону от рассматриваемого наклонного сечения, т.е. на расстоянии от опоры 112,5 см, равная 63,08 кН.
Поперечная сила, воспринимаемая поперечными проволоками сетки по формуле (61), равна:
Qm = qmωaq,
где aq - проекция наклонной трещины под углом 45°.
aq = 1200 - 50 = 1150 мм = 1,15 м;
μmωt - коэффициент приведенного армирования стенки при расчете на поперечную силу, равный
μmωt = μ'm + μsωtRsω/Rm = 0,0047 + 0,00284×270 : 206 = 0,0084,
qmω = Rmωμmωttω/sin(90° - β) = 206×0,0084×74,6 : 0,8042 = 160,5 Н×мм,
где β - угол наклона к вертикальной оси элемента.
Поперечная сила, воспринимаемая поперечными проволоками сетки, равна:
Qm = 160,5×1150 = 184595 Н = 184,6 кН.
Поперечная сила, воспринимаемая бетоном сжатой зоны в наклонном сечении, определяемая по формуле (64),
Qb = 0,75Rbttωh2ω/aq = 0,75×1,25×74,6×11002 : 1150 = 73,5 кН.
Q = 63,8 кН < 184,6 + 73,5 = 258,1 кН.
Следовательно, прочность сечения по наклонной трещине на действие поперечной силы обеспечена.
Расчет по предельным состояниям второй группы
Расчет по образованию трещин, нормальных к продольной оси элемента.
Для определения пластического момента сопротивления приведенного сечения вычисляем коэффициенты:
приведенного армирования с учетом модулей упругости сетки и бетона
α = Em/Eb = 150000 : 24500 = 6,12;
стержневой арматуры и сетки для верхней полки и стенки Es/Em = 170000/150000 = 1,13;
для нижней растянутой полки Ep/Em = 200000/150000 = 1,33.
Приведенные коэффициенты армирования
μ'mf(E) = μ'm + μsEs/Em = 0,0019×1,13 + 0,00284 = 0,005;
μmf1(E) = μmf + μsEs/Em = -0,00284 + 0,0227×1,33 = 0,0331;
μmω1(E) = μmω1 + μsEs/Em = 0,0047 + 0,0024×1,13 = 0,0074.
Приведенная площадь сечения
Ab = b'ft'f(1 + αμ'mf(E)) + tωhω(1 + αμmω1(E)) + bftf(1 + αμmf1(E)) = 300×50(1 + 6,12×0,005) + 74,6×1100(1 + 6,12×0,0074) + 300×500(1 + 6,12×0,033) = 119160 мм2.
Статический момент приведенной площади сечения относительно нижней грани
Sb = b'ft'f(1 + αμmt(E))(h - t'f/2) + tωhω(1 + μmω(E))(h - t'f - hω/2) + bftf(1 + αμmf1(E))tf/2 = 300×50(1 + 6,12×0,005)(1200 - 50 : 2) + 74,6×1100(1 + 6,12×0,0074)(1200 - 1100 - 50) + 300×50(1 + 6,12×0,0033)50 : 2 = 7,07×107 мм3.
Расстояние от центра масс до нижней грани
yc = Sb/Ab = 7,07×107 : 119160 = 588 мм.
Момент инерции сечения относительно центра массы приведенного сечения
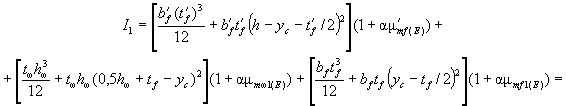
= [300×503 : 12 + 300×50(1200 - 588 - 50 : 2)2](1 + 6,12×0,0057) + [74,6×11003 : 12 + 1100×74,6(0,5×1100 + (50 - 588)2](1 + 6,12×0,0074) + [300×503 : 12 + 300×50(588 - 50 : 2)2](1 + 6,12×0,0033) = 1,916×109 мм4.
В соответствии со СНиП 2.03.01-84 предварительное напряжение в арматуре назначаем из условия
σsp + P ≤ Rs, ser,
где
P = 0,05σsp,
σsp = Rs, ser/1,05 = 1175 : 1,05 = 1119 МПа.
В соответствии с п. 1.38:
потери предварительного напряжения, возникающие от релаксации напряжений стали
σ1 = (0,22σsp/Rs, ser - 0,1)σsp = (0,22×1119 : 1175 - 0,1)1119 = 123 МПа,
потери от температурного перепада при Δt = 65°
σ2 = 1,25Δt = 1,25×65 = 81,2 МПа;
потери от деформации анкеров при расстоянии между упорами 20 м
σ3 = ΔtEs/l = 2×20×104 : 20000 = 20 МПа.
и потери от быстронатекающей ползучести бетона, подвергнутого тепловой обработке,
σ6 = 40σbp/0,85Rbp - коэффициент для бетона, подвергнутого тепловой обработке.
Принимаем значение Rbp при 70 %-ной прочности Rbp = 0,8×40 = 28 МПа, при α = 0,25 + 0,025Rbr = 0,95.
Предварительное напряжение на уровне центра тяжести арматуры определяется с учетом первых потерь σ1 + σ2 + σ3 = 123 + 81 + 20 = 224 МПа; σsp - (σ1 + σ2 + σ3) = 1119 - 224 = 895 МПа.
Усилие обжатия P за вычетом потерь по формуле (1) равно:
P = γspAsp[σsp - (σ1 + σ2 + σ3)] = 1×340×895 = 306000 Н.
ecp = yc - ap = 588 - 25 = 563 мм.
Напряжения в бетоне от преднапряжения равны:
σbp = P/Ab + P1ecp/I1 = 306000 : (1,916×102) + 303000×563 : (1,916×109) = 7,5 МПа.
Суммарная величина первых потерь σ1 + σ2 + σ3 + σ6 = 123 + 81 + 20 + 8 = 232 МПа. Преднапряжение с учетом первых потерь σsp1 = 1119 - 232 = 887 МПа. Усилие обжатия P1 с учетом первых потерь
P1 = γspAsp[σsp - (σ1 + σ2 + σ3)] = 1×340(1119 - 232) = 301,6 кН.
Вторые потери по табл. 3 равны:
от усадки мелкозернистого бетона σ8 = 52 МПа;
от ползучести мелкозернистого бетона при α = 0,85
σ9 = 150×1,3σbpα/Rbp = 150×1,3×7,5×28 : 0,85 = 44,4 МПа;
при σbp/Rbp = 7,5/28 = 0,26 < 0,75.
Вторые потери, вычисленные по табл. 3, равны:
σ8 + σ9 = 52 + 44,4 = 96,4 МПа.
Напряжения σsp2 с учетом всех потерь равны:
σsp2 = σsp - 232 - (σ8 + σ9) = 1119 - 232 - 96,4 = 790,6 МПа.
Усилие предварительного обжатия с учетом всех потерь при γsn = 1 равно:
P2 = γsnAspσsp2 = 1×340×790,6×104 = 268,8 кН.
Расчет по образованию трещин, нормальных к продольной оси складки
Момент сопротивления для растянутой грани приведенного сечения от внешней нагрузки и от предварительного обжатия соответственно равен:
Wf = I1/yc = 1,916×1010 : 588 = 32584×103 мм3;
W'f = I1/(h - yc) = 1,916×1010 : (1200 - 588) = 31307×103 мм3.
Расстояние от центра масс приведенного сечения до верхних и нижних ядровых точек
r = φWf/Ab;
r' = 0,7Wf/Ab = 0,7×32584×103 : (1191×102) = 19,1 мм;
rf = 0,7W'f/Ab = 0,7×31307×102 : (1191×102) = 18,4 мм.
где φ = 1,6 - σb/Rb, ser = 1,6 - 30 : 29 = 0,5, принимаем φ = 0,7.
Максимальное напряжение в сжатом бетоне, вычисляемое как для упругого тела по приведенному сечению, равно:
σb = P2/Ab + M/Wf = 268,8×104 : 119160 + 267,3×105 : (32584×103) = 0,3 МПа.
Вычисляем момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин в стадии эксплуатации по формуле (67), равный:
Mcrc = RbtWpl + Mshr.
Момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый по формуле (79),
Wpl = [0,292 + 0,75(γ1 + 2μmf1(E)) + 0,75(γ'1 + 2μ'mf(E))]tωh2 = [0,292 + 0,75(0,125 + 2×0,033×6,12) + 0,75(0,251 + 2×0,033×6,12)]74,6×12002 = 76497×103 мм3,
где
γ1 = (bf - tω)tf/(tωh) = (300 - 74,6)50 : (74,6×1200) = 0,125;
γ'1 = 2(b'f - tω)tf/(tωh) = 2(300 - 74,6)50 : (74,6×1200) = 0,251.
Момент, вызванный усадкой Mshr относительно верхней ядровой точки, вычисляем из следующей зависимости:
Mshr = P2(r' + lcp),
где расстояние от равнодействующего усилия до центра тяжести приведенного сечения равно:
lcp = yc - an = 588 - 25 = 563 мм;
an = tf/2.
Тогда момент от усадки
Mshr = 265047(19,1 + 563) = 199,84×106 Н×мм.
После подстановки в формулу (67) момент трещинообразования
Mcrc = 2,1×76497×103 + 268805(563 + 19,1) = 36,5×106 Н×мм = 365 кН×м.
Так как Mn = 267,3 кН м < Mcrc = 365 кН×м, следовательно, в эксплуатационной стадии работы складки трещин в ней не будет.
Поэтому расчет на раскрытие трещин не производится. Определяем возможность образования трещин в верхней зоне, растянутой в стадии изготовления и монтажа.
Момент сопротивления в этом случае относительно верхней растянутой грани с учетом неупругих деформаций бетона по формуле (79) равен:
W'crc = [0,292 + 0,75(γ1 + 2μ'mf(E)) + 0,75(γ'1 + 2μmf1(E))]tωh2 = [0,292 + 0,75(0,125 + 2×0,005×6,12) + 0,075(0,251 + 2×0,033×6,12)]74,6×12002 = 49624×103 мм3,
где γ1 = (b'f - t'ω)t'f/(tωh) = (300 - 74,6)50 : (74,6×1200) = 0,125;
γ'1 = 2(bf - tω)tf/(tωh) = 2(300 - 74,6)50 : (74,6×1200) = 0,251.
Момент от предварительного напряжения в верхней зоне сечения за вычетом нормативного момента от собственного веса Mn = 109700 кН×м равен:
Mp1 = P1/(lcp + rf) - Mn = 306000(563 - 18,1) - 109700 = -3,34 кН×м.
Так как момент от предварительного напряжения в верхней зоне меньше Rbt, serWcrc = 1,8×49624×10 = 89,3 кН×м, при Rbt, ser = 1,8 МПа и при Rbp = 0,7×40 = 28 МПа (по интерполяции). Следовательно, трещины в верхней зоне не будут раскрываться.
Расчет по образованию трещин, наклонных к продольной оси складки
Проверяем, образуются ли трещины в пределах зоны передачи напряжения. Длина зоны передачи напряжений (по СНиП 2.03.01-84) равна
lp = (ωpσsp/Rbp + λp)d = (0,25×892 : 32 + 10)6 = 102 мм,
где σsp = σsp1 = 892 МПа, Rbp = 0,8×40 = 32 МПа, d - диаметр проволоки 6 мм.
Так как зона передачи предварительного напряжения находится в пределах опоры, рассматриваем сечение при lx/lp = 1.
Напряжения на уровне центра тяжести приведенного сечения при y = 0 и P = P2 равны:
σ'x = P2/Ab = 265047 : (1191×102) = 2,2 МПа.
Сжимающее напряжение при вычислении σmt и σmc принимаем со знаком «минус». Для вычисления касательных напряжений τxy определяем статический момент части сечения, расположенной выше оси, проходящей через центр тяжести, относительно этой оси, который равен:
S'b = b'ft'f(1 + αμ'mf(E))(h - t'f/2 - yc) + 0,5tω(hω + tf - yc)2(1 + αμmω(E)) = 300×50(1 + 6,12×0,005)(1200 - 50 : 2 - 588) + 0,5×74,6(1100 + 50 - 588)2(1 + 6,12×0,0074) = 21388×103 мм3.
Скалывающие напряжения при максимальном значении поперечной силы равны:
τ = QS'b/(I1tω) = 6,38×21388 : (1,916×103×74,6) = 0,71 МПа.
Напряжение в бетоне σx на уровне центра тяжести (при y = 0) зависит от усилия обжатия, вычисленного с учетом потерь. При отсутствии поперечной предварительно напряженной арматуры σyn = 0.
Местные сжимающие напряжения σyM в месте приложения опорной реакции
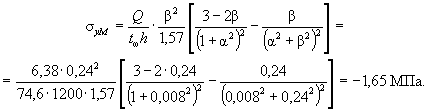
где α = x/h = 100 : 1200 = 0,08;
β = yc/h = 58,8 : 1200 = 0,24.
Главные сжимающие и растягивающие напряжения равны:
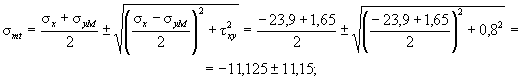
σmc = -0,37 + 0,88 = +0,51 МПа;
σmt = -0,37 - 0,88 = -1,25 МПа.
Тогда σmc = 0,51 МПа < Rb, ser = 0,5×22,5 = 11,25 МПа; σmt = -1,25 МПа < Rbt, ser = 1,8 МПа.
Таким образом, трещиностойкость наклонных сечений обеспечена.
Расчет прогибов складки
Жесткость складки Bf1 при кратковременном действии нагрузки по формуле (96)
Bf1 = 0,85EbI1 = 0,85×24500×1,916×1010 = 39,9×1013 Н×мм2.
Жесткость Bf2 при учете продолжительного действия нагрузки по формуле (101)
Bf2 = 0,85Bf1 = 39,9×1013×0,85 = 33,9×1013 Н×мм2.
Кривизна от кратковременного действия нагрузки по формуле (99)
ρ1 = Mn/Bf1 = -267×106 : (33,9×1013) = 7,12×10-7 мм-1.
Кривизна от постоянных и длительно действующих нагрузок по формуле (100)
ρ2 = Mnφb2/Bf2 = 210,6×106×2,6 : (33,9×1013) = 16×10-7 мм-1.
Коэффициент, учитывающий влияние ползучести бетона при влажности воздуха 40 %, принимаем равным 2,0 (п. 4.16). Кривизна от выгиба складки от действия предварительного обжатия по формуле (102)
ρ3 = P2lcp/Bf1 = 268805×563 : (39,9×1013) = 3,79×10-7 мм-1.
Кривизна от выгиба складки вследствие усадки и ползучести от предварительного обжатия по формуле (103)
ρ4 = (Σb - Σ'b)/h = 60,2×10-5 - 33,8×10-5 : 1200 = 2,2×10-7 мм-1.
Для вычисления деформаций εb, вызванных усадкой и ползучестью бетона под действием усилия предварительного обжатия, определяем напряжения в бетоне на уровне крайнего сжатого волокна, которые равны:
σ'bp = P1/A - Plcp(h - yc)/I1 - Mn(h - yc)/I1 = 303000 : (1191,6×1012) - 303000×563(1200 - 588) : (1,916×1010) - 109,7×106(1200 - 588) : (1,916×1010) = -633 МПа.
Растягивающие напряжения в бетоне, потери от быстропротекающей ползучести равны нулю: σ6 = 0; σ9 = 0, тогда σb = σ'b = 67,6 МПа. Деформации сжатия бетона равны:
ε'b = σ'b/Es = 67,6 : 200000 = 33,8×10-5;
εb = σbp2/Es = (σ6 + σ8 + σ9)/Es = 8 + 67,6 + 44,8 : (2×105) = 60,2×10-5.
Полная кривизна изгибаемой складки, в которой трещины не раскрываются, равна:
ρtot = ρ1 + ρ2 - ρ3 - ρ4 = 7,1×10-7 - 3,73×10-7 + 16×10-7 - 2,2×10-7 = 17,1×10-7 мм-1.
Полный прогиб складки при l0 = 18000 - 200 = 17800 мм по формуле (117) равен:
f = Sρtotl20 = 0,104×17,1×10-7×178002 = 56,6 мм.
Коэффициент S = 5/48 = 0,104 принимаем по табл. 15. Полученный прогиб складки составляет от пролета f/l0 = 56,6/17800 = 1/314 < [1/250], т.е. прогиб складки меньше допустимого.
ПРИЛОЖЕНИЕ 3
Пример расчета плиты-складки подвесного потолка*
* Пример расчета плиты-складки подвесного потолка разработан в НИИСКе (канд. техн. наук В.Д. Галич, инж. Т.В. Борисова).
Дано. Плита складчатая шириной 2,4 м, длиной 5,8 м, высотой 0,3 м (рис. 1), изготовленная из мелкозернистого бетона группы А, класса бетона по прочности на сжатие В40. Конструкция армируется двумя ткаными сетками № 10-1 (ГОСТ 3826-82*) по всему сечению разделительной сварной сеткой из проволочной арматуры класса Вр-I (ГОСТ 6727-80*) Æ 3 мм с шагом 200 мм в продольном направлении панели и Æ 4 мм с шагом 100 мм в поперечном. В продольных бортовых ребрах дополнительно устанавливаются стержни из горячекатаной арматуры периодического профиля класса А-III (ГОСТ 5781-82*) Æ 12 и Æ 16 мм в каждом ребре. Панель-складка эксплуатируется в отапливаемом помещении с относительной влажностью воздуха до 60 % и при отсутствии возможности систематического увлажнения конструкции конденсатом. В соответствии с условиями эксплуатации и принятым армированием панель относится ко 2-й категории трещиностойкости.
Рис. 1. Сечение складки подвесного потолка
а - фактическое; б - приведенное; в - схема усилий и эпюра напряжений
Нагрузки
Данные по виду распределенных нагрузок, их величинам и коэффициентам перегрузки, принятым в соответствии со СНиП 2.01.07-85, приведены в таблице.
|
Нагрузки, Н/м |
|||
|
вид |
нормативная |
коэффициент надежности |
расчетная |
|
Постоянные |
|
|
|
|
Собственная масса панели-складки 11500/2,4×5,8 |
826 |
1,1 |
909 |
|
Масса акустической облицовки |
80 |
1,2 |
96 |
|
Временные длительные |
|
|
|
|
Масса сплинкерной сетки, светильников |
250 |
1,2 |
300 |
|
Итого длительно действующие |
1156 |
- |
1305 |
|
Кратковременные |
|
|
|
|
Дополнительная нагрузка к массе оборудования |
700 |
1,3 |
910 |
|
Итого временные |
700 |
- |
910 |
|
Полная нагрузка |
1856 |
- |
2215 |
Плита складчатая должна воспринимать сосредоточенную технологическую нагрузку (давление колеса тележки на площадку 10 ´ 10 см) величиной 3000 Н с коэффициентом надежности по перегрузке.
1.2. Расчетная сосредоточенная нагрузка
P = 3000×1,2 = 3600 Н.
Определение усилий
Складка в целом рассчитывается как однопролетная шарнирно опертая балка пролетом 5,7 м (рис. 2).
Определяем моменты от следующих сочетаний нагрузок:
1. Действие полной распределенной расчетной нагрузки (рис. 2)
M = (q + q)bL2/8 = (1305 + 910)2,4×5,72 : 8 = 21599 Н×м.
Рис. 2. Расчетная схема складки подвесного потолка
а - схема нагрузок; б - расчетная нагрузка; в - расчетная схема
2. Действие части расчетной распределенной нагрузки и временной расчетной сосредоточенной
M = qbL2/8 + pL/4 = 1305×2,4×5,72 : 8 + 3600×5,7 : 4 = 17850 Н×м.
Так как решающим является первое сочетание, то для этого случая определяем все остальные усилия:
момент от полной нормативной нагрузки
Mn = (qn + qn)bL2/8 = (1156 + 700)2,4×5,72 : 8 = 18090 Н×м;
момент от длительно действующей части нормативной нагрузки
Mn = qnbL2/8 = 1156×2,4×5,72 : 8 = 11267 Н×м;
расчетная перерезывающая сила (на опоре)
Q = (q + q)bL/2 = (1305 + 910)2,4×5,7 : 2 = 15150 Н.
Характеристики материалов
Бетон мелкозернистый группы А, подвергнутый тепловой обработке при атмосферном давлении, класс бетона по прочности на сжатие В40: расчетное сопротивление бетона сжатию для предельных состояний первой группы Rb = 22,5 МПа; то же для предельных состояний второй группы Rb, ser = 29 МПа; расчетное сопротивление бетона растяжению для предельных состояний первой группы Rbt = 1,4 МПа; то же для предельных состояний второй группы Rbt, ser = 2,1 МПа; начальный модуль упругости при растяжении и сжатии Eb = 2,4×104 МПа.
Арматура - сетки тканые № 10-1 ГОСТ 3826-82*; расчетное сопротивление продольных проволок и поперечных проволок растяжению при расчете нормальных наклонных сечений на действие изгибающего момента Rm = 245 МПа; то же поперечных проволок при расчете наклонных сечений на действие поперечной силы Rmω = 206 МПа; расчетное сопротивление сжатию Rmc = 235 МПа; модуль упругости Em = 1,5×105 МПа.
Сетки сварные армируются из проволоки класса Вр-I диаметром 3 мм; расчетное сопротивление растяжению при расчете нормальных и наклонных сечений на действие изгибающего момента Rs = 375 МПа; то же при расчете наклонных сечений на действие поперечной силы Rsω = 305 МПа; расчетное сопротивление сжатию Rsc = 375 МПа; расчетное сопротивление для расчета по предельным состояниям второй группы Rs, ser = 410 МПа; модуль упругости Es = 1,7×105 МПа.
Стержневая арматура класса А-III диаметром более 10 мм (название характеристики см. выше):
Rs = 365 МПа; Rsω = 295 МПа; Rsc = 365 МПа; Rs, ser = 410 МПа; Es = 2×105 МПа.
РАСЧЕТ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
Расчет по прочности сечения, нормального к продольной оси
Для расчета фактическое сечение элемента приводим к двутавровому (см. рис. 1). Толщина стенки двутаврового сечения равна:
tω = δn/sinβ = 2,2 : 0,42578 = 9,4 см.
Ширина сжатой полки b'f, вводимая в расчет в соответствии с. п. 3.10. При отсутствии поперечных ребер и при t'f1 = 2 см < 0,1h = 0,1; b'f = 2×6t'f + tω = 2×6×2 + 9,4 = 33,4 см.
Вычисляем коэффициент сетчатого армирования
μm = 0,0071×2 : 2 = 0,0071.
Коэффициент приведенного армирования равен:
для сжатой полки
μ'mf1 = μm + μsRsc/Rmc = 0,0071 + 0,00213×375 : 245 = 0,0103;
μs = As, tot = 2×0,071 : (2×3,34) = 0,00213;
для стенки μmω1 = μ'mf1 = 0,0105;
для растянутой полки тканую и сварную сетку приводим к сетчатой с коэффициентом армирования, равным:
μm1 = μmf1 + μsfRs/Rm = 0,0071 + 0,000355×375 : 245 = 0,0076;
μsf = 3×0,071/40×15 = 0,000355;
усилия от стержневой арматуры учитываем отдельно.
Сечение рассчитываем в соответствии с п. 3.5. Граничное значение высоты сжатой зоны по формуле (8) равно:
ξR = ω/[1 + σs(1 - ξn/1,1)/400],
где ω = 0,7 - 0,008Rb = 0,7 - 0,008×22,5 = 0,520; σs = Rs = 365 МПа.
После подстановки в формулу (8) предельное отношение высоты сжатой зоны
ξR = 0,52/1 + 365/400(1 - 0,52/1,1) = 0,35.
Высота сжатой зоны x из условия (22)
Rcf1Acf + Rcω1Acω = Rmμmf1Atf + Rmμmω1Atω + RsAs,
где Rsf1 = Rb + RmcμEmf1 = 22,5 + 245×0,0105 = 24,96 МПа;
Rcω1 = Rb + Rmcμmω1 = 22,5 + 245×0,0105 = 24,96 МПа;
Acf = b'ft'f = 33,4×2 = 66,8 см2;
Atf = bftf = 600 см2;
Acω = (x - t'f)tω = (x - 2)9,4 см2;
Atω = (h - x - tf)tω = (15 - x)9,4 см2.
После подстановки полученных величин в формулу (22) высота сжатой зоны равна.
24,96×66,8 + 24,96(x - 2)9,4 = 245×0,0014×600 + (15 - x)9,4 + 365×6,28x = 1432,3/244 = 5 см.
Таким образом, ξ = x/h = 5,8/30 = 0,193 < ξn = 0,35, а нейтральная ось проходит в стенке.
Прочность сечения определится из условия (17)
M ≤ Rcf1Acf(h - t'f/2-a) + Rcω1Acω1[h - (x + 2a + tf)/2 - Rmμmω1Atω[(h - x)/2 - a] - Rmμmf1Abft[(tf - a)/2] = 24,96×66,8(30 - 2 : 2 - 3) + 24,96×9,4[30 - (5,9 + 6 + 2) : 2] - 245×0,0105(15 - 5,9)[(30 - 5,9) : 2 - 3] - 245×0,0014×480[(15 - 3) : 2] = 63291 Н×м,
где Abft = bf(tf - a) = 40(15 - 3) = 480 мм2.
Таким образом, прочность нормального сечения обеспечивается, так как M = 21590 Н×м < 63291 Н×м.
Расчет прочности сечения, наклонного к продольной оси
Проверяем условие (57), обеспечивающее прочность по сжатому бетону между наклонными трещинами (п. 3.24),
Q ≤ 0,3φω1φb1Rbbhω,
где φω1 = 1 + Emμmω1/Eb = 1 + 1,5×105×0,0105 : (2,4×104) = 1,984;
φb1 = 1 - 0,01Rb = 1 - 0,01×22,5 = 0,775; tω = 9,4 см.
После подстановки величин в формулу (57) получаем равенство: 0,3×1,984×775×22,5×9,4×11 = 1073 МПа×см2 = 107300 Н.
Прочность по сжатому бетону между наклонными трещинами обеспечивается, так как Q = 15150 Н < 107300 Н.
Необходимость расчета наклонного сечения по прочности на перерезывающую силу проверяем из условия 0,4×1,4×8,4×27 = 142 МПа×см2 = 14200 Н.
Так как Q = 15150 Н > 14200 Н, то расчет на перерезывающую силу необходимо выполнить. Прочность наклонного сечения должна проверяться из условия (60)
Q ≤ Qm + Qb.
Значение поперечной силы Qm, воспринимаемой поперечными проволоками сетки, пересекающими наклонную трещину, по формуле (61) равно:
Qm = qmωaq.
При угле наклона трещины 45° интенсивность армирования элемента поперечными проволоками сеток в пределах наклонной трещины по формуле (62) равна:
qmω = Rmωμmω1tω/sinβ = 206×0,0105×9,4 : sin 64°48' = 2250 Н×см.
Значение поперечной силы равно Qm = 2250×30 = 67500 Н.
Поперечная сила, воспринимаемая бетоном, определяется по формуле (64)
Qb = 0,75Rbttωh2/aq = 0,75×1,4×9,4×302 : 30 = 29600 Н.
Прочность наклонного сечения на поперечную силу достаточная, так как: Q = 15150 Н < Qm + Qb = 67500 + 29600 = 97100 Н.
РАСЧЕТ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
Расчет по образованию трещин, нормальных к продольной оси
Для определения пластического момента сопротивления приведенного сечения вычисляем:
коэффициенты приведенного армирования с учетом отношений модулей упругости:
сжатой полки
μ'mf1(E) = μm + μsEs/Em = 0,0071 + 0,00213×2×105 : (1,5×105) = -0,00993;
стенки
μmω1(E) = μ'mf1(E) = 0,00993;
растянутой полки (с учетом отношений модулей стержневой арматуры)
μmf1(E) = μmf + μsfEs/Em + AsEs/(bftfEm) = 0,000835 + 0,000355×2×105 : (1,5×105) + 6,28×2×105 : (40,15×1,5×105) = 0,0151.
Отношения модулей упругости равны:
α = Em/Eb = 1,5×105 : (0,24×105) = 6,25;
αs = Es/Eb = 2×105 : (0,24×105) = 8,3.
Приведенная площадь сечения
A1 = b'ft'f(1 + αμ'mf1(E)) + tωhω(1 + αμmω1(E)) + bftf(1 + αμmf1(E)) + αsAs = 100×2(1 + 6,25×0,00993) + 9,4×13(1 + 6,25×0,00993) + 40×15(1 + 6,25×0,00131) + 6,28×8,3 = 988,3 см2.
Статический момент приведенной площади сечения относительно нижней грани
S1 = bft'f(1 + αμmf1(E))(h - t'f/2) + tωhω(1 + αμmω1(E))(h - t'f - hω/2) + bftf(1 + αμmf1(E))tf/2 + αsAs = 212,4(30 - 2 : 2) + 119,8(30 - 2 - 13 : 2) + 604×15 : 2 + 52,1×3 = 13422 см3.
Расстояние от центра массы сечения до нижней грани
ycm = S1/A1 = 13422 : 988,3 = 13,6 см.
Момент инерции сечения относительно центра массы равен:
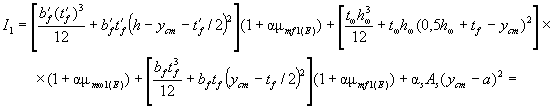
= [100×23 : 12 + 100×2(30 - 13,6 - 2 : 2)2](1 + 6,25×0,00993) + [9,4×133 : 12 + 9,4×13(0,5×13 + 15 + 13,6)2](1 + 6,25×0,00993) + [40×153 : 12 + 40×15(13,6 - 15 : 2)2](1 + 6,25×0,00131) + 6,28×8,3(13 - 3)2 = 101344 см4.
Согласно табл. 13 для двутаврового несимметричного сечения при отношениях δ ≥ bf/b = 100/9,4 = 10,6 и tf/h = 15/30 = 0,5 > 0,3 коэффициент γ = 1,5.
Пластический момент сопротивления приведенного сечения по формуле (80)
Wpl = γW0 = γI1/ycm = 1,5×101344 : 13,6 = 11344 см3.
Изгибающий момент, воспринимаемый сечением, нормальным к продольной оси панели, равен:
Мсrс = 0,75WpiRbt, ser = 0,75×11344×2,1 = 17867 МПа/см3 = 17867 Н < Mn = 18090 Н×м.
Следовательно, в стадии эксплуатации трещины возникают.
Расчет по раскрытию трещин, нормальных к продольной оси
В соответствии с п. 4.9 ширина раскрытия трещин при комбинированном армировании определяется по формуле (85)
acrc =
φφсγmηmσm/Em120(3,5
- 100μmf1)![]() ,
,
где φ = 1 (для изгибаемых элементов); φe = 1 при учете кратковременных и непродолжительного действия постоянных и длительных нагрузок; φс = 1,5 - для бетона группы А при учете продолжительного действия постоянных и длительных нагрузок; γm = 4,5 при μm1 = 0,08 % < 1 %; ηm = 1,1 - для тканых сеток;
μmf1 = 0,0014 + 6,28/40×15×365/235 = 0,0176;
μs = As/(bftf) = 6,28 : (40×15) = 0,0104.
Приведенный модуль упругости по формуле (87)
Em1 = (Emμm + Esμs)/(μm + μs) = (1,5×105×0,0071 + 2×105×0,0104) : (0,0071 + 0,0104) = 1,8×105 МПа.
Диаметр проволочной арматуры при различных диаметрах стержней и проволок сеток по формуле (86)
ds = (n1d21 + n2d22)/(n1d1 + n2d2) = (2×122 + 2×162) : (2×12 + 2×16) = 14,28 мм.
Напряжение в сетке для изгибаемых элементов без предварительного напряжения по формуле (87)
σm = M/Ws1,
где Ws1 - момент сопротивления сечения, приведенного к стальному, вычисляемый по формуле (91):
Ws1 = Is1/1,3ycm.
Для определения положения центральной оси в момент трещинообразования вычисляем статический момент площади приведенного таврового сечения (без полок в растянутой зоне) относительно нижней грани.
S'2 = b'ft'f(1 + αμ'mf(E))(h - t'f/2) + tω(hω + tf)(1 + αμmω(E))(hω + tf /2) + αsAsa = 100×2(1 + 6,25×0,00993)(30 - 2 : 2) + 9,4(13 + 15)(1 + 6,25×0,00131)(13 + 15) : 2 + 6,28×83×3 = 10031 см3.
Приведенная площадь таврового сечения
A'2 = b'ft'f(1 + αμmf(E)) + tω(hω + tf)(1 + αμmω(E)) + AsLs = 100×2(1 + 6,25×0,00993) + 9,4(13 + 15)(1 + 6,25×0,00131) + 6,28×83 = 529 см2.
Приведенная площадь уширений растянутой полки
Arb = (bf - tω)tf(1 + αμmf(E)) = (40 - 9,4)15(1 + 6,25×0,00131) = 463 см2.
Высота сжатой зоны в момент трещинообразования по формуле (78)
h - x = S'r/(A'2 + Arb/2) = 10031 : (529 + 463 : 2) = 13,2 см,
откуда x = h - 13,2 = 30 - 13,2 = 10,8 см. Размеры сечения, приведенного к стальному, равны следующим величинам:
высота сжатой полки (рис. 3)
t'sf1 = μ'mf1(E)t'f + t'fEb/Em1 = 0,00993×2 + 2×2,4×104 : (1,8×105) = 0,286 = 0,3 см;
толщина сжатой стенки
tscω1 = μmω1(E)tω + tωEb/Em1 = 0,00993×9,4 + 9,4×2,4×104 : (1,8×105) = 1,35 см;
толщина растянутой стенки
tstω1 = μmω1(E)tω = 0,00993×9,4 = 0,1 см;
толщина растянутой полки
tsf1 = μmf1(E)tf = 0,0151×15 = 0,227 = 0,23 см.
Так как центры тяжести стальных полок совпадают с центрами тяжести растянутой и сжатой арматуры, то общая высота стального сечения
hs1 = h - (a + a) + 0,5(t'sf1 + tsf1) = 30 - (0,8 + 0,8) + 0,5(0,3 + 0,23) = 29 см.
Рис. 3. Сечение, приведенное к стальному
а - расчетное сечение; б - сечение, приведенное к стальному
Высота сжатой зоны x1 = x - 0,5t'f = 16,8 - 0,5×2 = 15,8 см.
Площадь стального сечения
Fs1 = b'ft'sf1 + (x1 - t'sf1)tscω1 + (hs1 - x1 - tsf1)tstω1 + bftstω1 = 100×0,3 + (15,8 - 0,3)1,3 + (29 - 15,8 - 0,23)0,1 + 40×0,23 = 60,65 см2.
Статический момент относительно нижней грани сечения
Ss1 = b'ft'sf1(hs1 - 0,5t'sf1) + (x1 - t'sf1)tscω1[hs1 - 0,5(x1 - t'sf1)] + (hs1 - x1 - tsf1)(tstω1[0,5(hs1 - x1 - tsf1) + tsf1] + bftsf1×tsf1/2 = 100×0,3(29 - 0,5×0,3) + (15,8 - 0,3)1,35[29 - 0,5(15,8 - 0,3)] + (29 - 15,8 + 0,23)0,1[0,5(29 - 15,8 - 0,23) + 0,23] + 40×0,23×0,23 : 2 = 1320 см3.
Расстояние до центра тяжести сечения
ycm = Ss1/Fs1 = 1320 : 60,65 = 21,8 см.
Момент инерции
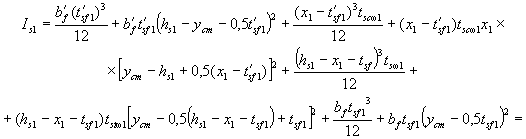
= 100×0,33 : 12 + 100×0,3(29 - 21,8 - 0,5×0,3)2 + (15,8 - 0,3)31,35 : 12 + (15,8 - 0,3)1,35×[21,8 - 29 + 0,5(15,8 - 0,3)2] + (29 - 15,8 - 0,23)30,1 : 12 + (29 - 15,8 - 0,23)0,1[21,8 - 0,5(29 - 15,8 - 0,23) + 0,23]2 + 40×0,233 : 12 + 40×0,23(21,8 - 0,5×0,23)2 = 6555 см4.
Момент сопротивления, приведенного к стальному, равен:
Ws1 = Is1/1,3ycm = 6555 : (1,3×21,8) = 231,3 см3.
Напряжения в растянутой зоне от кратковременного действия полной нагрузки
σm = Mn/Ws1 = 1809000 : 231,3 = 78,2 МПа.
Напряжения от кратковременного действия постоянных к длительных нагрузок
σm = Mnдл/Ws1 = 1126700 : 231,3 = 48,7 МПа.
Для определения ширины кратковременного раскрытия трещин вычисляем величины acrc1, acrc2, acrc3.
Ширина раскрытия трещин от кратковременного действия полной нагрузки
acrc1 =
φφсγmηm(σm/Em1)20(3,5
- 100μmf1)![]() = 1×1×4,5×1×78,2
: (1,8×105)20(3,5
- 100×0,0176)14,28
= 0,164 мм.
= 1×1×4,5×1×78,2
: (1,8×105)20(3,5
- 100×0,0176)14,28
= 0,164 мм.
Ширина раскрытия трещины от кратковременного действия постоянных и длительных нагрузок
acrc2 = 1×1×4,5×1![]() 20(3,5 - 100×1,0176)14,28 = 0,101 мм.
20(3,5 - 100×1,0176)14,28 = 0,101 мм.
Ширина раскрытия трещин от длительного действия постоянных и длительных нагрузок
acrc3 =
1×1,5×4,5×1![]() 20(3,5 - 100×0,0176×14,28)
= 0,152 мм.
20(3,5 - 100×0,0176×14,28)
= 0,152 мм.
Ширина кратковременного раскрытия трещин
acrc = acrc1 - acrc2 + acrc3 = 0,164 - 0,101 + 0,152 = 0,215 = 0,2 мм.
Величина длительной ширины раскрытия трещин acrc3 = 0,152 @ [acrc2] = 0,15 мм.
Таким образом, ширина раскрытия трещин не превышает величин, допускаемых для конструкций, относящихся ко 2-й категории трещиностойкости.
Расчет по образованию трещин, наклонных к продольной оси
Для изгибаемых элементов расчет производим из условий (81):
при σmc ≤ γbcRb, ser, σmt ≤ Rbt, ser;
при σmc > γbcRb, ser,
![]()
γbc - коэффициент условий работы, определяемый по формуле
γbc = 0,8 - αB ≤ 0,5,
где α = 0,02 для мелкозернистых бетонов;
В - класс бетона 40 МПа; γbc = 0,8 - 0,02×40 = 0; принимаем γbc = 0,5.
Расчет производим на уровне центра тяжести приведенного сечения и в месте примыкания сжатой полки к стенке по формуле (83)
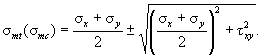
Статический момент части сечения, расположенной выше оси, проходящей через центр тяжести всего сечения (рис. 47) относительно этой оси, равен:
Sr = b'ft'f(1 + αμmf1(E))(h - ycm - 0,5t'f) + tωhω(1 + αμmf1(E))(h - ycm - 0,5hω - t'f ) + bf(tf - ycm)(1 + αμmf1(E))0,5(tf - ycm) = 100×2(1 + 6,25×0,00993)(30 - 13,6 - 0,5×2) + 9,4×13(1 + 6,25×0,00993)(30 - 13,6 - 0,5×1,3 - 2) + 40(15 - 13,6)(1 + 6,25×0,00131)0,5(15 - 13,6) = 4281 см3.
Касательные напряжения на уровне центра тяжести сечения
τxy = QSr/(Irb) = 15150×4281 : (101344×40) = 0,16 МПа.
На оси, проходящей через центр тяжести сечения, главные растягивающие напряжения равны:
σmc = τxy = 0,16 МПа; < Rbt, ser = 2,1 МПа,
а главные сжимающие напряжения
σmc = -τxy = -0,16 МПа < γb6Rb, ser = 0,5×29 = 14,5 МПа.
Следовательно, трещиностойкость по наклонному сечению обеспечена.
Расчет деформации
Прогиб изгибаемого элемента с постоянным сечением определяем по формуле (117)
f = mρtotl2,
где по табл. 15 m = 5/48; пролет l = 5,7 м;
полное значение кривизны изгибаемого элемента по формуле (106)
ρtot = ρ5 - ρ6 + ρ7.
Величина ρ5, определяемая по формуле (107), равна
ρ5 = Mcrc/Bf1 + (Mn - Mcrc)/Bf3,
где Mcrc = 17867 Н×м; Mn = 18090 Н×м; Bf1 = 0,85EbIr1 = 0,85×2,4×104×101344 = 2,067×109 МПа×см4; Bf3 = kEbIr1 = 0,08×2,4×104×101344 = 0,165×109 МПа×см4, K = 0,08, μm1 = 0,99 % < 1,5 %; тогда
ρ5 = 1786700/2,061×1011 + (1809000 - 1786700)/0,165×1011 = 0,997×10-5 см-1.
Значение ρ6 по формуле (112)
ρ6 = Mcer/Bf3 = 1126700 : (0,165×1011) = 6,828×10-5 см-1,
где Mcer = 11267 Н×м, Bf3 = 0,165×109 МПа×см4. Значение ρ7 по формуле (113)
ρ7 = Mcer/B'f3 = 1126700 : (0,132×1011) = 8,536×10-5 см-1,
где B'f3 = 0,8, Bf3 = 0,8×0,165×109 = 0,132×109 МПа×см4. Полная кривизна по формуле (106)
ρtot = (0,997 - 6,828 + 8,536)10-3 = 2,705×10-5 см-1.
Прогиб по формуле (117)
f = 5/48×2,705×10-5×5702 = 0,916 см.
Так как f = 0,916 см < 1/250l = 1/250×570 = 2,28 см, то жесткость панели достаточна.
ПРИЛОЖЕНИЕ 4
Расчет плиты-оболочки в поперечном направлении *
* Пример расчета плиты-оболочки в поперечном направлении разработан НИИСКом (канд. техн. наук В.Д. Галич, инж. Т.В. Борисова).
Дано: Размеры сечения, общие данные и нагрузки приведены в примере расчета панели-складки в целом.
Определение усилий
Статический расчет в поперечном направлении производим с учетом следующих предпосылок:
1. При соотношении пролетов l1/l2 = 5,7/2,4 = 2,375 рассматриваемая отнесена к длинным.
2. В соответствии с требованием Руководства по проектированию железобетонных тонкостенных пространственных конструкций покрытий и перекрытий (М.: Стройиздат, 1979) при расчете на равномерно распределенную нагрузку принимаем расчетную схему и виде трехпролетной плиты шириной 1 м с соответствующими поправочными коэффициентами на внутренние усилия.
3. При расчете на сосредоточенную силу также принимаем расчетную схему в виде трехпролетной плиты шириной 1 м. Эта предпосылка основана на исследовании работы железобетонных плит в предельном состоянии под действием сосредоточенной нагрузки (Дубинский А.М. Расчет несущей способности железобетонных плит и оболочек - Киев. Будивельник, 1976).
Расчетные схемы панели-складки в поперечном направлении прияты в соответствии с изложенными выше предпосылками.
Расчетный момент в поперечном направлении определяем из рассмотрения следующих сочетаний нагрузок:
1. Постоянные и временные длительные (именуемые далее постоянными), а также временные, распределенные на трех пролетах.
2. Постоянные и временные, распределенные на двух смежных пролетах.
3. Постоянные и временные, распределенные на среднем пролете.
4. Постоянные и временная, сосредоточенная в середине среднего пролета.
Моменты определяем с помощью табл. 14.18 - 14.20 для неравнопролетных плит и балок (Улицкий И.И. и др. Железобетонные конструкции: Расчет и конструирование. - Киев: Будивельник, 1972) и поправочных коэффициентов табл. 5 Руководства по проектированию железобетонных тонкостенных пространственных конструкций покрытий и перекрытий (М.: Стройиздат, 1979).
Сочетание 1 (рис. 1)
Момент на опоре
Mb = Mc = -K2N1/K3 + L2N2/K3;
K2 = K1 = 2(l2 - l3) = 2(1 + 0,35) = 2,7;
K3 = K1K2 - l22 = 2,7×2,7 - 12 = 6,29;
N1 = N2 = (q1 + q1)(l31 + l32)/4 = (1305 + 910)(0,353 + 13) : 4 = 578 Н;
Mb = N1(l2/K3 - K2/K3) = 578(1 : 6,29 - 2,7 : 6,29) = -156 Н×мм.
При отношении высоты торцевого элемента h1 к высоте складки (h) h1/h = 15/30 = 0,5 принимаем по линейной интерполяции поправочный коэффициент для опорного момента 1,833.
Таким образом, опорный момент Mb = (-156)1,833 = -286 Н×мм.
Момент в пролете
M2 = (q2 + q2)l22/8 - Mb = (1305 + 910)12 : 8 - 156 = 121 Н мм.
Рис. 1. Расчетные схемы складки подвесного потолка при расчете в поперечном направлении
а - схема для определения моментов на опорах; б - схема для определения момента в пролете
Сочетание 2
Моменты на опорах равны:
Mb = -K2N1/K3 + l2N2/K3;
Mc = l2N1/K3 - K1N2/K3.
где K1 = K2 = 2,7; K3 = 6,29 (см. выше); N1 = 578 (см. выше).
N2 = (q2 + q2)l32l33q3/4 = (1305 + 910)13 + 1305×0,353 : 4 = 568 Н;
Mb = -2,7/6,29×578 + 1/6,29×568 = -158 Н×мм;
Mc = 1/6,29×578 - 2,7/6,29×568 = -152 Н×мм.
С учетом поправочного коэффициента (см. выше): Mb = (-158)1,833 = -290 Н×мм; Mc = (-152)1,833 = -279 Н×мм. Момент в пролете
M2 = (q2 + q2)L22/8 - (Mb + Mc)/2 = (1305 + 910)12 : 8 - (158 + 152) : 2 = 122 Н×мм.
Сочетание 3
Моменты на опорах
Mb = Mc = -K2N1/K3 + L2N2/K3,
где K2 = 2,7; K3 = 6,29;
N1 = N2 = [q1l31 + (q2 + q2)L32]/4 = 1305×0,353 + (1305 + 910)13 : 4 = 568 Н;
Mb = Mc = -2,7/6,29×568 + 1/6,29×568 = -154 Н×мм.
С учетом поправочного коэффициента Mb = Mc = (-154)1,833 = -290 Н×мм. Момент в пролете
M2 = (q2 + q2)l22/8 - Mb = (1305 + 910)12 : 8 - 154 = 123 Н×мм.
Сочетание 4
Моменты на опоре от равномерно распределенной нагрузки
Mb = Mc = -K2N1/K3 + l2N2/K3,
где K2 = 2,7; K3 = 6,29;
N1 = N2 = (q1l31 + q2l32)/4 = (1305×0,353 + 1305×13) : 3 = 340 Н;
Mb = Mc = -2,7/6,29×340 + 1/6,29×340 = -92 Н×мм.
Момент от сосредоточенной нагрузки Mb = Mc = -K2/K3N1, где K2 = 2,7; K3 = 6,29;
N1 = 3PL22/8 = 3×3600×0,352 : 8 = 165 Н;
Mb = Mc = -2,7/6,29×165 = -71 Н м.
Суммарный опорный момент
ΣMb = ΣMc = -92 + (-71) = -163 Н×мм.
Суммарный опорный момент с учетом поправочного коэффициента
ΣMb = ΣMc = (-163)1,833 = -300 Н×мм.
Момент в пролете (с учетом перераспределения усилий)
M2 = q2L22/8 + Pl/6 - ΣMb = 1305×1 : 8 + 3600×1 : 6 - 163 = 600 Н×мм.
Таким образом, решающей нагрузкой при расчете плиты-оболочки в поперечном направлении является сосредоточенная нагрузка, а расчетный момент под силой в середине средней грани равен 600 Н×мм. По этому моменту проверяем сечение армоцементной складки.
Момент от полной нормативной нагрузки
M2 = 1156×12/8 + 3000×1/6 - (92/1,1 + 71/1,2) = 501 Н×мм.
Момент от длительно действующей части нормативной нагрузки
Mncer = 1156×12/8 = 144 Н×мм.
Расчет по прочности сечения, нормального к продольной оси
Вычисляем коэффициент приведенного армирования. Сечение армировано двумя сетками № 10-1 и сварной соткой 200/100/3/4 (рис. 2)
μm1 = μm + μsRsc/Rmc = 0,0071×2 : 2 + 0,0063×375 : 235 = 0,0171,
где μs = As, tot/4 = 10×0,126 : 2×100 = 0,0063.
Сечение рассчитываем в соответствии с п. 3.5.
Граничное значение высоты сжатой зоны по формуле (8)
ξR = ω/[1 + σs(1 - ω/1,1)/400],
где ω = 0,7 - 0,008Rb = 0,7 - 0,008×22,5 = 0,32; σs = Rm = 235 МПа;
![]()
Высота сжатой зоны x из условия (11)
x = Rmμm1h/(Rc1 + Rmμm1) = 235×0,0171×2 : (26,5 + 235×0,00171) = 0,263 см,
где Rc1 = Rb + Rmμm1 = 22,5 + 235×0,0171 = 26,5 МПа. Так как ξ = x/h = 0,263/2 = 0,131 < ξR = 0,194, несущая способность сечения, определяемая по формуле (10), равна:
M ≤ Rmμm1Abth/2,
где Abt = (h - x)b = (2 - 0,263)100 = 174 см2; M = 245×0,0171×174×2/2 = 699 МПа/см2 = 700 Н×мм. Таким образом, прочность сечения обеспечивается, так как M = 600 Н×мм < 700 Н×мм.
Расчет на продавливание
Расчет на продавливание от действия сил, равномерно распределенных на ограниченной площади, производим из условия
P ≤ kPmμm1bcph.
При определении величин, входящих в условие, принимаем, что сосредоточенная нагрузка передается на площадке 10 ´ 10 см и продавливание происходит по боковой поверхности пирамиды, наклонные грани которой образуют с горизонтом 45° (рис. 3).
Рис. 2. Горизонтальная грань складки подвесного потолка
а - схема армирования в продольном направлении; б - схема армирования в поперечном направлении; в - схема усилий и эпюра напряжений в поперечном направлении; г - сечение, приведенное к стальному, в поперечном направлении
Рис. 3. Схема пирамиды продавливания
При определении коэффициента армирования, приведенного к сетке, в растянутой зоне учитываем армирование полки плиты-оболочки в продольном направлении. Это армирование состоит из сварной сетки, в продольном направлении которой стержни имеют меньший диаметр и расположены с большим шагом.
Коэффициент армирования
μm1 = μm + μsRc/Rm = 0,0071 + 0,001775×375 : 235 = 0,0099,
где
μs = As, tot/A = 5×0,71 : (2×100) = 0,001775.
Коэффициент K принимаем для тяжелых бетонов равным 1.
Среднее арифметическое параметров верхнего и нижнего основания пирамиды продавливания равно: Bcp = 4(10 + 14)/2 = 48 см.
Нагрузка, воспринимаемая боковой поверхностью пирамиды продавливания, равна: 1,235×0,0099×48,2 = 223 МПа = 22300 Н/м, что больше P = 3600 Н, следовательно, прочность на продавливание обеспечена.
Расчет по образованию трещин, нормальных к продольной оси элемента
В соответствии с п. 4.3 момент инерции относительно центра тяжести приведенного сечения
I1 = bh3/12 = 100×23 : 12 = 66 см4.
Момент сопротивления сечения
W0 = I1/ycm = 66 : 1 = 66 см3.
Пластический момент сопротивления приведенного сечения по формуле (80) равен: Wpl = γW0 = 1,75×66 = 115,5 см3.
Момент, воспринимаемый сечением, нормальным к продольной оси по формуле (67), равен: Mcrc = 0,75WplRbt, ser = 0,75×66×2,1 = 104 Н×мм < Mn = 501 Н×мм. Следовательно, трещины будут возникать.
Расчет по раскрытию трещин, нормальных к продольной оси
В соответствии с п. 4.8 ширина раскрытия трещин по формуле (84)
acrc = ηmφcσmSm/Em1,
где η = 3,5; φc = 1 при учете кратковременных и непродолжительного действия постоянных и длительных нагрузок; φc = 1,5 для бетона группы А при учете продолжительного действия постоянных и длительных нагрузок Sm = 10 мм.
Приведенный модуль упругости арматуры по формуле (87)
Em1 = (Emμm + Esμs)/(μm + μs) = (1,5×105×0,0071 + 1,7×105×0,0063)(0,0071 + 0,0063) = 1,59×105 МПа.
Напряжение σm для изгибаемых элементов без предварительного напряжения определяем по формуле (89)
σm = M/Ws1.
Момент сопротивления сечения, приведенного к стальному по формуле (91), равен:
Ws1 = Is1/1,3ys.
Для определения размеров сечения, приведенного к стальному, определяем положение нейтральной оси по формуле
x = h – Sr/F'r.
Приведенная площадь сечения
F'r = Fb + Fm + Em/Eb + F'mEm/Eb + FsEs/Eb = 100×2 + 0,71×15×104 : (2,4×104) + 0,71×15×104 : (2,4×104) + 1,26×17×104 : (2,4×104) = 217,8×102 мм2.
Статический момент относительно растянутой грани
Sr = 0,5hFb + 0,4FmEm/Eb + 1,6E'mEm/Eb + 0,8FsEs/Eb = 0,5×2×200 + 0,4×4,44 + 1,6×4,44 + 0,8×8,9 = 216×103 мм3.
Высота сжатой зоны
x = 2 - 216/217,8 = 1,01×10 мм.
Размер сечения, приведенного к стальному (рис. 2), равен:
высота сжатой зоны
hs1 = μm1(E)x + Ebx/Em1 = 0,0142×1 + 24×104×1 : (15,9×104) = 0,165×10 мм.
Коэффициент армирования
μm1(E) = μm + μsEs/Em = 0,0071 + 0,0063×1,7×105 : (1,5×105) = 0,0142×10 мм.
Высота растянутой зоны
hs1 = μm1(E)(h - x) = 0,0142×1 = 0,014×10 мм.
Для вычисления геометрических характеристик совмещаем верх сжатой зоны с верхней гранью расчетного сечения и растянутую зону с центром тяжести растянутой тканой сетки (см. рис. 49).
Вычисляем геометрические характеристики сечения, приведенного к стальному:
площадь
Fs1 = h's1b + hs1b = 0,165×100 + 0,014×100 = 17,9×102 мм2;
статический момент относительно нижней грани сечения
Ss1 = h's1b(h - h's1/2) = 0,165×100(1,6 - 0,165 : 2) = 25×103 мм3;
расстояние до центра тяжести
ycm = Ss1/Fs1 = 25 : 17,9 = 1,4×10 мм;
момент инерции
Is1 = (h's1)3/12 + h's1b(h - ycm - h's1/2)2 + hs1b(ycm - hs1/2)2 = 0,1653×100 : 12 + 0,165×100(1,6 - 1,4×0,165 : 2)2 + 0,0142×100(1,4 - 0,0142 : 2)2 = 3,015×104 мм4.
Момент сопротивления сечения, приведенного к стальному по формуле (97), равен:
Ws1 = Is1/1,3ycm = 3,015 : (1,3×1,4×10) = 1,66×103 мм3.
Напряжение в растянутой зоне от кратковременного действия полной нагрузки по формуле (89)
σm = Mn/Ws1 = 50100 : 1,66 = 302 МПа;
от кратковременного действия постоянных и длительных нагрузок
σm = Mnser/Wm1 = 14400 : 1,66 = 86,7 МПа.
Для определения ширины кратковременного раскрытия трещин вычисляем acrc1, acrc2, acrc3.
Ширина раскрытия трещин от кратковременного действия полной нагрузки
acrc1
= 3,5×1![]() 10 = 0,066 мм.
10 = 0,066 мм.
Ширина раскрытия трещин от кратковременного действия постоянных и длительных нагрузок
acrc2
= 3,5×1![]() 10 = 0,019 мм.
10 = 0,019 мм.
Ширина раскрытия трещин от длительного действия постоянных и длительных нагрузок
acrc3
= 3,5×1,5![]() 10 = 0,028 мм.
10 = 0,028 мм.
Кратковременная ширина раскрытия трещин по формуле (92)
acrc = acrc1 - acrc2 + acrc3 = 0,066 - 0,019 + 0,028 = 0,075 < acrc1 = 0,2 мм.
Величина длительного раскрытия трещин acrc3 = 0,028 мм < [acrc2] = 0,15 мм. Таким образом, ширина раскрытия трещин не превышает величин, допускаемых в соответствии с табл. 1 для конструкций, относящихся ко 2-й категории трещиностойкости.
Расчет по деформациям
Прогиб изгибаемого элемента с постоянным сечением по формуле (117)
f = mρtotL2,
где по табл. 15 m = (8 + 5)0,362/(2 + 0,362)48 = 0,0866; L = 1000 мм;
K = ql/P = 1305×1 : 3600 = 0,362.
Полное увеличение кривизны элемента по формуле (106)
ρtot = ρ5 - ρ6 + ρ7.
Кривизна ρ5 по формуле (107)
ρ5 = Mcrc/Bf1 + (Mn - Mcrc)/Bf3,
где Mcrc = 104 Н×м; Mn = 501 Н×м. Жесткость по формуле (96)
Bf1 = 0,85E1I1 = 0,85×2,4×104×66 = 134,6×104 МПа×см4.
Жесткость по формуле (108)
Bf3 = kEbI1 = 0,16×2,4×104×66 = 25,3×104 МПа×см4.
где k = 0,16 при μm1 = 1,71 % > 1,5 %. После подстановки в формулу (107) кривизна ρ5 равна:
ρ5 = 10400/134,6×106 + (50100 - 10400)/25,3×106 = 1,64×10-3 см-1.
Кривизна ρ6 по формуле (112)
ρ6 = Mcer/Bf3 = 14400 : (25,3×106) = 0,57×10-3 см-1.
Кривизна ρ7 по формуле (113)
ρ7 = Mcer/B'f3 = 14400 : (20,24×106) = 0,71×10-3 см-1,
где жесткость B'f3 = 0,8Bf3 = 0,8×25,3×104 = 20,24×104 МПа×см4. Полная кривизна по формуле (106) ρtot = (1,647 - 0,57 + 0,71)10-3 = 1,787×10-3 см-1. Прогиб по формуле (117) f = 0,0866×1,787×10-3×1002 = 1,55 см. Прогиб с учетом перераспределения усилий f = 4/6×1,55 = 1 см. Это составляет 1/170 полного пролета складки в поперечном направлении и меньше 1/150 пролета для второстепенных элементов перекрытий.
ПРИЛОЖЕНИЕ 5
Пример расчета трехшарнирного свода пролетом 12 м из армоцементных элементов волнистого профиля
Исходные данные. Пролет свода 12 м, стрела подъема в ключе 6 м, ширина свода 2 м. Свод используется для покрытия неотапливаемого здания, относится ко II категории трещиностойкости.
Свод изготовлен из мелкозернистого бетона класса по прочности на сжатие В30 группы А, марка по морозостойкости F150, марка по водонепроницаемости W6.
Нормативные сопротивления бетона для предельных состояний I группы (табл. 6) равны: Rbn = 22 МПа - осевое сжатие; Rbtn = 1,8 МПа - осевое растяжение.
Расчетные сопротивления бетона для предельных состояний I группы (табл. 7) равны: Rb = 17 МПа; Rbt = 1,2 МПа.
Коэффициенты условий работы бетона равны: γb1 = 0,9 (табл. 9); γb5 = 0,85 (табл. 9).
Расчетные сопротивления бетона для предельных состояний II группы (табл. 6) равны. Rb, ser = 22 МПа; Rbt, ser = 1,8 МПа.
Начальный модуль упругости мелкозернистого бетона при сжатии и растяжении определяем по табл. 10: Eb = 23×103 МПа.
Волнистый свод армируется: двумя слоями тканой сетки № 8-0,7 (ГОСТ 3826-82*) по всей длине, двумя слоями тканой сетки № 10-1 (ГОСТ 3826-82*) в полках.
Расчетные сопротивления сеток для предельных состояний I группы (табл. 11) равны:
Rm = 245 МПа - растяжение продольных проволок (при расчете по изгибающему моменту);
Rmω = 206 МПа - растяжение поперечных проволок (при расчете по поперечной силе);
Rmc = 245 МПа - сжатие.
Начальный модуль упругости сеток принимается по п. 2.25 Em = 15×104 МПа.
Нормативное сопротивление растяжению для предельных состояний I группы Rsn = 390 МПа.
Расчетные сопротивления для предельных состояний I группы равны растяжению: Rs = 335 МПа - для расчета по изгибающему моменту; Rsω = 285 МПа - для расчета по поперечной силе; Rsc = 355 МПа - на сжатие.
Расчетное сопротивление растяжению для предельных состояний II группы равно: Rs, ser = 390 МПа.
Начальный модуль упругости стержневой арматуры Es = 2×105 МПа.
Расчетная схема принята в виде трехшарнирной арки волнистого постоянного сечения пролетом 12 м и высотой 6 м.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СВОДА (рис. 1)
Сбор нагрузок
1. От собственного веса qпcb = 1350/8,917 = 151,4 кг/м = 1514 Н/м, qcb = 151,4×1,1 = 167 кг/м = 1670 Н/м.
2. Снеговая нагрузка для III снегового района при n = 1,4:
а) равномерно распределенный снег c1 = l/(8f) = 12/(8×6) = 0,25 < 0,4, следовательно, c1 = 0,4; p = p0cn×2 = 100×0,4×1,4×2 = 112 кг/м = 1120 Н/м;
б) неравномерный снег f/c = 6/12 = 1/2 > 1/8, следовательно, c2 = 2,2; p = p0cn×2 = 100×2,2×1,4×2 = 616 кг/м = 6160 Н/м.
3. Ветровая нагрузка II ветровой район, n = 1,2f/l = 0,5, следовательно, c2 = -1,2; c3 = -0,4; c1 = 0,7.
Расчетные ветровые давления:
q1 = 35×0,7×1,2 = 29,4 кг/м2 = 294 Н/м2;
q2 = 35×1(-1,2)1,2 = -50,4 кг/м2 = 504 Н/м2;
q3 = 35×1(-0,4)1,2 = -16,8 кг/м2 = -168 Н/м2.
4. Подвесное оборудование
P = (500 + 100)1,2 = 720 кг = 7200 Н.
Рис. 1. Геометрическая характеристика свода
IV. РАСЧЕТ АРМОЦЕМЕНТНОГО СВОДА ШИРИНОЙ 2 м
В соответствии со статическим расчетом для подбора сечения принято следующее сочетание усилий: M = 11,33 кН×м; N = -40 кН; Q = 3,82 кН.
Для расчета на действие поперечной силы принимаем Q = 12,62 кН, действующую в опорном сечении (точка 0).
Приводим поперечное сечение свода (рис. 2) к двутавровому (рис. 3):
δ = 18 + 21,2/2 = 19,6 мм; β = 26°; sin(90 - β) = sin(90 - 64°) = 0,4384;
tω = 2δ/sin(90° - β) = 2×19,6 : 0,4384 = 89,4 мм - толщина стенки.
Принимаем tω = 90 мм:
Aω = tωhω = 90×230 = 20700 мм2 - площадь стенки;
Abfc = b'ft'f = 300×35 = 10500 мм2 - площадь сечения сжатой полки;
Рис. 2. Поперечное сечение волны арки
1 - арматура верхней и нижней полки стержневая Æ 6 А-III; 2 - тканые сетки верхней и нижней полки (два слоя № 10-1); 3 - два слоя тканой сетки стенки № 10-1
Рис. 3. Расчетное сечение свода приведенное
1 - стержневая арматура верхней и нижней полки (1 Æ А-III); 2 - два слоя тканой сетки стенки № 10-1
Abft = bftf = 300×35 = 10500 мм2 - площадь сечения растянутой полки;
Ab = Aω + Abfc + Abft = 20700 + 10500 + 10500 = 41700 мм2 - площадь бетона в поперечном сечении.
Расчет по предельным состояниям I группы
Вычисляем коэффициенты армирования: коэффициент приведенного армирования растянутой полки
μmf1 = μmf + μsfRs/Rm;
где μmf - коэффициент сетчатого армирования растянутой полки;
μmf = μmf1 + μmf2 = Am1/tf + Am2/tf = 2×0,00385×102×0,115 : 35 + 2×0,00785×102×0,091 : 35 = 0,00661,
где μmf1 = Am1/tf - коэффициент сетчатого армирования растянутой полки сеткой № 8-0,7; μmf2 = Am2/tf - то же, сеткой № 10-1, где Am1, Am2 - площадь сечения сеток на единицу длины в растянутой полке соответственно № 8-0,7, № 1 (см. прил. 2 СНиП 2.03.03-85); Am1 = 0,00385×102×0,115 = 0,0442 мм2/мм; Am2 = 0,00785×102×0,091 = 0,0714 мм2/мм; μsf = As/Abft = 4×0,283×102/35×300 = 0,01078 - коэффициент армирования растянутой полки стержневой арматурой, где As - площадь сечения стержневой арматуры, As = 4×0,283×102 = 113,2 мм2.
Коэффициент приведенного армирования верхней растянутой полки μmf1 = 0,00661 + 0,01078×355/245 = 0,0222. Коэффициент приведенного армирования сжатой полки μ'mf1.
Так как армирование симметричное, μ'mf1 = μmf1 = 0,0222, где μ = 0,01973 - коэффициент приведенного армирования стенки;
μmω = Amω/tω = 4×0,00385×102×0,115 : 39,9 = 0,0045,
где Amω - площадь сечения сеток на единицу длины в стенке.
Эксцентриситет продольной сжимающей силы от всей расчетной нагрузки
e0 = M/N = 1130000 : 40000 = 298 мм > ea,
где ea - случайный эксцентриситет, обусловленный не учтенными в расчете факторами (п. 3.15).
Значение ea принимается равным:
ea = la/600 = 8,917 : 600 = 0,015 м = 15 мм,
где la - длина части элемента между точками закрепления;
ea = h/30 = 300 : 30 = 10 мм;
h - высота сечения элемента.
Принимаем e0 = 1048 мм. Учет влияния прогиба элемента (п. 3.16), формула (29)
η = 1/(1 - N/Ncr).
Условная критическая сила
Ncrt
= 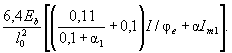
Момент инерции бетонного сечения относительно центра масс бетонного сечения
![]()
Момент инерции всей арматуры относительно центра масс бетонного сечения
Im1 = EsIs/Em + Imf1 + Imf,
где Is, Imf1, Imf - моменты инерции соответственно стержневой арматуры, сетчатой арматуры верхней полки, сетчатой арматуры нижней полки, равные:
Imf1 = Imf = 2×105/15×104×2×113,2(150 - 35/2)2 + 2×0,00661×10500(150 - 35/2)2 = 7736630 мм4.
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, равен:
φe = 1 + βM1e/M1, при β = 1,3.
Моменты внешних сил относительно оси M1 и M1e, проходящей через растянутую грань сечения от действия полной нагрузки и от действия постоянной и длительной нагрузки, равны;
M1 = полная + N/(h0 - a')/2 = 11,33 + 10,81(0,3 - 0,018)/2 = 11,33 + 1,52 = 12,85 кН×м;
M1e = 0,2 + 0,3×5,93 + (8,22 + 0,3×6,89)(0,3 - 0,018)/2 = 0,2 + 1,78 + 1,45 = 3,43 кН×м.
После подстановки коэффициенты равны:
φe = 1 + 3,43/12,85×1,3 = 1,35;
α1 = e0/h = 104,8/300 = 3,49 > α1min = 0,02515,
где α1min = 0,5 - 0,01l0/h - 0,01Rb = 0,5 - 0,01×10344/300 - 0,01×17×0,9×0,85 = 0,5 - 0,3448 - 0,13005 = 0,02515. Расчетная длина l0 = 0,58la = 0,58×8917 = 5172 мм. Принимаем α1 = 3,49. Отношение модуля упругости сетчатой арматуры Em и бетона Eb равно:
α = Em/Eb = 15×104 : (23×103) = 6,52.
Критическая сила
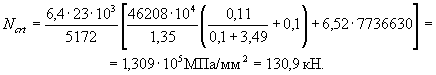
Коэффициент увеличения эксцентриситета η = 1/(1 - 40/130,9) = 1,44.
Эксцентриситет расчетной силы с коэффициентом, учитывающим влияние продольного изгиба, равен: ec = e0×η = 29,8×1,44 = 43 см.
Для определения, по какому случаю следует рассчитывать внецентренно сжатое сечение, определяем предельное отношение x/h. Предельное отношение x/h по формуле (8)
ξR = ω/[1 + σs(1 - ω/1,1)/σsc, u].
Характеристика сжатой зоны для внецентренно сжатого сечения по формуле (9) ω = 0,5 - 0,008Rb = 0,5 - 0,008×17×0,9×0,85 = 0,396. Напряжение в арматуре σs = Rs = 355 МПа; предельное напряжение в арматуре сжатой зоны σsc, u = 500 МПа (СНиП 2.03.01-84, п. 3.12)
После подстановки величин в формулу (8) получим ξn = 0,396/1 + 355/500(1 - 0,396/1,1) = 0,27. Эксцентриситет продольной силы N относительно нижней растянутой грани
et = ec + ycm = 43 + 15 = 58 см.
Эксцентриситет продольной силы N относительно сжатой полки
e' = et - h + tf/2 = 58 - 30 + 1,5 : 2 = 29,5 см.
Коэффициент γ1 по формуле (48)
γ1 = (et - h)(b'ft'f - tωt'f) - tω(t'f)2/2 + b'f(t'f)2/2 = (58 - 30)(30×3,5 - 9×3,5) - 9×3,52 : 2 + 3×3,52 : 2 = 2023,2.
Коэффициент γ2 по формуле (48)
γ2 = γ1μmω + b'ft'f(μmc1 - μmω)e' = 0,0071×2023,2 + 30×3,5(0,0222 - 0,0071)33,2 = 66,8.
Коэффициент γ3 по формуле (49)
γ3 = tωμmω(het - h2/2 - tfet + t2f/2) + bftfμmf1(et - tf/2) = 9×0,0071(30×58 - 30 : 2 - 3,5×58 + 3,52 : 2) + 30×3,5×0,0222(58 - 35 : 2) = 201.
После подстановки полученных величин в формулу (47) получим
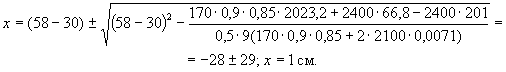
Поскольку отношение высоты сжатой зоны x/h = 0,033 < ξR = 0,27; x = 10 мм, t'f = 35 мм, прочность внецентренно сжатого сечения по формуле (33) равна:
N'e ≤ Rmμmω1Aω(hω + tf)/2 + Rmμmf1At[h - (tf + t'f)/2] = 245×0,0071×20700(230 + 35) : 2 + 245×0,0222×10500×300 - (35 + 35) : 2 = 19930000 Н×мм.
Прочность сечения N = 19930000/295 = 67500 Н = 67,5 кН. Прочность сечения обеспечена, так как N = 67,5 > 40 кН.
Расчет по прочности сечений, наклонных к продольной оси элемента, производится по сжатому бетону между трещинами по формуле (57):
Q ≤ 0,3φω1φb1Rbbhω.
Коэффициент, учитывающий влияние поперечных и продольных проволок сеток по формуле (58), равен:
φω1 = 1 + 5Emμmω1/Eb = 1 + 5×15×104 : (23×103×0,002) = 1,065.
Коэффициент приведенного армирования стенки при расчете на поперечную силу по формуле (63)
μmω1 = Amω/(tωhω) + Asω(Rsω/(hωtωRmω) = 0,002.
Поперечные стержни, пересекающие наклонную трещину, отсутствуют. Коэффициент φb1 по формуле (59) φb1 = 1 - 0,01Rb = 1 - 0,01×17×0,9×0,85 = 0,987. Максимальная поперечная сила в опорном сечении Q = 12,62 кН.
После подстановки величин в формулу (57) получим 0,3φω1φb1Rbbhω = 0,3×1,065×0,987×17×0,9×0,85×90×230 = 82278 МПа/мм2 = 82,3 кН > Q = 12,62 кН, т.е. условие выполнено.
Расчет прочности сечений, наклонных к продольной оси, выполняем по формуле (60).
Поперечная сила, воспринимаемая поперечными проволоками сетки, пересекающих наклонную трещину, по формуле (61). Проекции наклонной трещины (угол наклона трещины принимается равным 45°) aq = 230 мм.
Интенсивность армирования элемента поперечными проволоками сеток в пределах наклонной трещины по формуле (62)
qmω = Rmωμmω1tω/sin(90 - β) = 206×0,002×90 : 0,4384 = 84,6 МПа = 8460 Н/м.
Угол наклона стенки к вертикальной оси сечения β = 64°; sin(90 - 64) = sin 26 = 0,4384. Поперечная сила Qm = 8460×0,23 = 1946 Н = 1,95 кН.
Поперечная сила, воспринимаемая бетоном сжатой зоны в наклонном сечении для внецентренно сжатого элемента по формуле (64), равна:
Qb = 0,75Rbttωh2ω/aq = 0,75×1,2×0,9×0,85×90×2302 : 230 = 14300 МПа×мм2 = 14,3 кН.
Прочность по наклонному сечению по формуле (60) Q = 12,62 < Qm + Qb = 1,95 + 14,3 = 16,25 кН. Условие выполнено.
Расчет по предельным состояниям II группы
Расчет внецентренно сжатого элемента по образованию нормальных трещин производим из условия (66): Mn ≤ Mcrc.
Момент внешних сил по формуле (71)
Mn = N(ec - rn).
Момент, воспринимаемый нормальным сечением при образовании трещин по формуле (67), равен:
Mcrc = Rbt, serWcrc ± Mshr.
Коэффициенты приведенного армирования с учетом отношения модулей упругости равны:
μmf1(E) = μ'mf1(E) = μmf + μsfEs/Em = 0,00661 + 0,01078×20×104 : (15×104) = 0,021;
μmω = μmω(E) = 0,002.
Приведенная площадь сечения
A1 = b'ft'f(1 + αμ'mf1(E)) + bftf(1 + αμmf1(E)) + tωhω(1 + αμmω(E)) = 2×300×35(1 + 6,52×0,021) + (1 + 6,52×0,002)90×230 = 44900 мм2.
Так как армирование симметричное, ycm = 150 мм. Момент инерции сечения относительно центра масс приведенного сечения
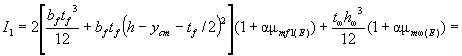 2[300×352 : 12 + 300×35(300
- 150 - 35 : 2)2](1 + 6,52×0,021)
+ 90×2303
: 12(1 + 6,52×0,002) = 51404×104
мм4.
2[300×352 : 12 + 300×35(300
- 150 - 35 : 2)2](1 + 6,52×0,021)
+ 90×2303
: 12(1 + 6,52×0,002) = 51404×104
мм4.
Момент сопротивления сечения W1 = I1/ycm = 51404×104/150 = 3427×103 мм3. Расстояние от центра масс приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется по формуле
rn = φW1/A1,
где 0,7 ≤ φ = 1,6 - σb/Rb, ser ≤ 1. Максимальное напряжение в сжатом бетоне, вычисляемое как для упругого тела по приведенному сечению, равно:
σb = N/A1 + M/W1 = 10,81 : 44900 + 11,33 : (3427×103) = 0,0274×10-2 кН/мм2 = 27,4 МПа;
φ = 1,6×27,4/22 = 0,655 < 0,7.
Принимаем φ = 0,7; rn = 0,7×3427×103/44900 = 53,4 мм.
Момент относительно ядровой точки Mn = N(ec - rn) = 10,81(11,42 - 53,4) = 11710 кН×мм = 11,77 < кН×м.
Момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона по формуле (79)
Wcrc = [0,292 + 0,75(γ1 + 2αμmf1(E)) + 0,75 (γ2 + 2αμ'mf1(E))]tωh2 = (0,292 + 0,75(0,272 + 2×0,021×6,52) + 0,075(0,544 + 2×0,021×6,52)90×3002 = 6172200 мм3,
где
γ1 = (bf - tω)tf/(tωh) = (300 - 90)35 : (90×300) = 0,272;
γ2 = 2(b'f - tω)t'f(tωh) = 2(300 - 90)35 : (90×300) = 0,544;
α = Em/Eb = 6,52.
Момент усилия Nshr, вызванного усадкой армоцемента, относительно той же оси, что и для определения M:
Mshr = Nshr(ecp + rn).
Усилие усадки по формуле (60)
Nshr = σshr(μmf1(E)Acf + μmf1(E)Aωt + μmf1(E)Aft).
Напряжение в сетке, вызванное усадкой бетона σshr, равное 45 МПа (для мелкозернистого бетона группы А класса В30, подвергнутого тепловой обработке), равно:
Nshr = 45(0,021×10500 + 0,021×10500 + 0,002×20700) = 21700 МПа/мм2 = 21,7 кН.
Эксцентриситет силы Nshr относительно центра масс приведенного сечения по формуле (70)
ecp = (μmf1(E)Aftyt + μmω1(E)Aωtyt - μ'mf1(E)Acfyc)/(μmf1(E)Aft + μmω1(E)Aωt + μ'mf1(E)Acf),
где yt = yc; yω = 0, следовательно, ecp = 0; yt, yω, yc - расстояния от центра масс приведенного сечения до центров масс сечений соответственно растянутой полки, вертикальной стенки и сжатой полки.
Момент от усадки Mshr = Nshrrn = 21,7×53,4 = 1159 кН×мм = 1,16 кН×м.
Момент, воспринимаемый сечением при образовании трещин по формуле (67), равен: Mcrc = 1,8×6172200×10 - 1,16 = 9,9 кН×м, так как Mn = 11,77 кН×м > Mcrc = 9,9 кН×м.
Рис. 4. Сечение свода, приведенное к стальному
Трещины в бетоне раскрываются. Ширину раскрытия трещин, нормальных к продольной оси элемента, при комбинированном армировании определяем по формуле (85)
acrc =
φφeηmγm(σm/Em)20(3,5
- 100μmt1)![]() ,
,
φ = 1 - внецентренно сжатый элемент, φe = 1 - при кратковременных нагрузках и кратковременном действии нагрузок; φe = 1,5 - при длительном действии нагрузок для мелкозернистого бетона группы А; γ = 1,5, так как μωt > 2 %; ηm = 1, так как сетки тканые.
Приведенный модуль упругости арматуры по формуле (87)
Em1 = (Emμm + Esμs)/(μm + μs) = (15×104×0,00661 + 2×105×0,01078) : (0,00661 + 0,01078) = 18,1×104 МПа.
Для вычисления ширины раскрытия трещины приводим сечение к стальному (рис. 4).
Для определения положения нейтральной оси в момент трещинообразования вычисляем статический момент площади таврового сечения (без полок в растянутой зоне) относительно нижней грани.
Статический момент сечения
Sтb = b'ftf(h - t'f/2)(1 + αμ'mf1(E)) + [tω(hω - tf)(hω + tf/2)](1 + αμmω1(E)) = 300×35(300 - 35 : 2)(1 + 6,52×0,021) + [90(230 + 35)(230 + 35) : 2](1 + 6,52×0,002) = 6573700 мм3.
Приведенная суммарная площадь таврового сечения
Aт1 = b'ft'f(1 + αμ'mf1(E)) + tω(hω + tf)(1 + αμmω1(E)) = 300×35(1 + 6,52×0,021) + 90(230 + 35)(1 + 6,52×0,002) = 36100 мм2.
Приведенная площадь уширений растянутой полки
Aym = (bf - tω)(1 + αμmf1(E))tf = (300 - 90)(1 + 6,52×0,021)35 = 8360 мм2.
Высоту сжатой зоны в момент трещинообразования определяем по формуле (78)
h - x = Sтb1/(Aт1 + A1ym/2) = 6573700 : (36100 + 8360 : 2) = 163,2 мм;
x = h - 163,2 = 300 - 163,2 = 136,8 мм = 137 мм.
Момент инерции сжатой зоны сечения относительно нулевой линии
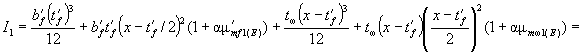 300×353 : 12 + 300×35(137
- 35 : 2)2(1 + 6,52×0,021) + 90(13,7 - 35)3 : 12 +
90(137 - 35)[(137 - 35) : 2]2(1 + 6,52×0,002)
= 203942800 мм4.
300×353 : 12 + 300×35(137
- 35 : 2)2(1 + 6,52×0,021) + 90(13,7 - 35)3 : 12 +
90(137 - 35)[(137 - 35) : 2]2(1 + 6,52×0,002)
= 203942800 мм4.
Статический момент растянутой части сечения относительно нулевой линии равен:
St1 = bftf(h - x - tf/2)(1 + αμmf1(E)) + tω(hω + tf - x)2(1 + αμmω1(E))/2 = 300×35(300 - 137 - 35 : 2)(1 + 6,52×0,021) + 90(230 + 35 - 137)2(1 + 6,52×0,002) : 2 = 2483820 мм3.
Момент сопротивления приведенного сечения с учетом неупругих деформаций растянутого бетона по формуле (76)
W1 = 2I1/(h - x) + S1 = 2×203942800 : 163 + 2483820 = 4986190 мм3.
Расстояние от центра масс до ядровой точки
r = W1/A1 = 4986190 : 44900 = 111,1 мм.
Размеры сечения, приведенного к стальному (рис. 4):
tsf1 = μmf1(E)tf = 0,021×35 = 0,74 мм;
tsωt1 = μmω1(E)tω = 0,002×90 = 0,18 мм;
t'sf1 = μ'mf1(E)t'f + t'fEb/Em = 0,021×35 + 35×23×103 : (15×104) = 6,1 мм;
t'sωc1 = μmω1(E)tω + tωEb/Em = 0,002×90 + 90×23×103 : (15×104) = 14 мм;
hs = h - (t'f + tf)/2 = 300 - (35 + 35) : 2 = 265 мм;
x1 = x - t'f/2 = 137 - 35 : 2 = 119,5 мм.
Расстояние до центра масс сечения, приведенного к стальному, равно:
yc = S1/A1 = [b'ft'sf1h1 + tsωc1x1(h1 - x1/2) + tsωt1(h1 - x1)2/2]/[b'ft'sf1 + t'sωc1x1 + tsωt1(h1 - x1) + bftsf1] = [300×6,1×265 + 1,4×119,5(265 - 119,5 : 2) + 0,18(265 - 119,5)2 : 2] : [300×6,1 + 1,4×119,5 + 0,18(265 - 119,5) + 300×0,74] = 221 мм.
Момент инерции сечения, приведенного к стальному, равен:
Is1 = b'ft'sf1(h1 - yc)2 + tsωc1x31/12 + tsωc1x1(h1 - x1/2 - yc)2 + tsωt1(h1 - x1)3/12 + tsωt1(h1 - x1)[yc - (h1 - x1)/2]2 + bftsf1y2c = 300×6,1(265 - 221)2 + 1,4×119,53 : 12 + 1,4×119,5(265 - 119,5 : 2 - 221)2 + 0,18(265 - 119,5)3 : 12 + 0,18(265 - 119,5)[221 - (265 - 119,5) : 2]2 + 300×0,74×2212 = 1741×104 мм4.
Момент сопротивления сечения, приведенного к стальному по формуле (91), равен:
Ws1 = Is1/1,3yc = 1741×104 : (1,3×221) = 60,6×103 мм3.
Напряжение в арматуре по формуле (90) σm = Ntot(ec tot ± r)/Ws1. Равнодействующая продольной силы равна N, так как усилие предварительного обжатия равно нулю.
Ширина непродолжительного раскрытия трещин определяется по формуле (92)
acrc = acrc1 - acrc2 + acrc3.
Для определения ширины раскрытия трещин от непродолжительного действия всей нагрузки acrc1 по формуле (85) вычисляем: при Mн1 = 8,75 кН×м, Nн1 = -35,81 кН; ec = 8,75/35,81 = 0,244 м = 244 мм; ec, tot = e0η = 244×1,44 = 351,4 мм;
σm1 = N(ec, tot - r)/Ws1 = 35,81(351,4 - 111,1) : (60,6×103) = 141,9 МПа.
Ширина раскрытия трещин по формуле (85)
acrc1 =
1×1×1,5×1![]() 20(3,5 - 100×0,02)
20(3,5 - 100×0,02)![]() = 0,064 мм.
= 0,064 мм.
Ширина раскрытия трещин от постоянных и длительных нагрузок при их непродолжительном действии равна: M2 = 6,45 кН×м; N2 = 28,90 кН.
Эксцентриситет ec = M2/N2 = 6,45/29,9 = 0,223 м = 223 мм; ec, tot = 223×1,44 = 321 мм.
Напряжение σm2 = 28,9(321 - 111,1)/60,6×103 = 100 МПа;
acrc2 =
1×1×1,5×1![]() 20×1,5
20×1,5![]() = 0,014 мм.
= 0,014 мм.
Ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок равна: acrc3 = 1,5acrc2 = 1,5×0,044 = 0,06 мм.
Кратковременное раскрытие трещин равно:
acrc = acrc1 - acrc2 + acrc3 = 0,064 - 0,044 + 0,06 = 0,08 мм.
Кратковременное раскрытие трещин не превышает допустимого раскрытия по табл. 1: acrc = 0,08 < [acrc1] = 0,1 мм.
Длительное раскрытие трещин равно допускаемому длительному раскрытию трещин (табл. 1) при применении оцинкованной сетки.
ПРИЛОЖЕНИЕ 6
Примеры технологии изготовления армоцементных конструкций
Изготовление армоцементных плит-оболочек методом стационарного виброштампования
Сравнительно небольшие в плане армоцементные конструкции площадью до 20 м2 с развитыми ребрами и сложным армированием оболочки, например, панели-оболочки подвесного потолка, целесообразно изготавливать методом стационарного виброштампования в двойной опалубке, разработанным в НИИСКе Госстроя СССР. Плита подвесного потолка представляет собой пологую длинную цилиндрическую оболочку, ограниченную по длине торцевыми диафрагмами, а по ширине - бортовыми элементами, вытянутыми в горизонтальном направлении. Такое очертание и размеры вызваны технологическими и эксплуатационными требованиями к устройству проходного чердака.
* Технологию изготовления и конструкцию армоцементных плит-оболочек разработали в НИИСКе (канд. техн. наук В.Д. Галич, В.Н. Овчар).
Плита-оболочка (рис. 1) имеет следующие размеры: длина 5,79 м, ширина 2,31 м, высота 0,3 м, толщина плиты 20 мм и армируется частыми сетками сварной сеткой и сварными каркасами. Плита изготавливается из мелкозернистого бетона группы А или Б, нижняя поверхность плиты окрашивается паронепроницаемой масляной или синтетической краской. Поле плиты-оболочки армируется пакетом, состоящим из одной сварной и двух тканых сеток. Проектное положение тканых сеток обеспечивалось применением разделительных сварных сеток. Бортовые элементы армируются пространственными каркасами, диафрагмы - плоскими каркасами. Для съема изделий с матрицы и последующих монтажных операций в торцах панелей-оболочек предусмотрены потайные петли. В бортовых элементах предусмотрены также закладные изделия для приварки к полкам ригелей и для крепления к панелям светильников.
Арматурные каркасы ребер свариваются на шаблоне в пространственный каркас. Защитный слой фиксируют скрутками, оставляемыми при вязке пакета сеток, предварительной раскладкой подстилающего слоя бетонной смеси, фиксаторами конструктивных сеток.
Формы оснастки состоят из комплекта металлических матриц и пуансонов. Доборные плиты половинной ширины могут размещаться по две в матрице с клиновой извлекаемой после формования перегородкой. Отверстия в плитах образуют вкладышами на матрицах. В верхних частях формы предусматривают участки для удаления избытка бетонной смеси.
Мелкозернистую бетонную смесь равномерно распределяют по матрице. Для получения ровной верхней поверхности при укладке необходимо дополнительное уплотнение смеси вибропрофилером. Поверх смеси устанавливают пуансон и пригруз, обеспечивающий удельное давление порядка 10-2 МПа.
Виброштампование на площадке с частотой 50 Гц и амплитудой не менее 0,4 мм производит до полной посадки пуансона на матрицу, но не менее 90 с. Затем снимают пригруз, удаляют избыток смеси, выдавленный сквозь центральную прорезь пуансона, а форму с изделием помещают в пропарочную камеру. Режим тепловой обработки в двойной опалубке аналогичен кассетному производству.
На посту распалубки, после снятия пуансона, плита-оболочка с помощью траверсы извлекается из формы-матрицы и укладывается в штабель с прокладками по углам. Транспортируют плиту в контейнерах с откидными опорами.
Трехгранная складчатая плита подвесных потолков (рис. 2) более удобна для прохода по ним в устройства световых проемов. Средняя горизонтальная грань плиты-складки имеет ширину 1 м. Опалубочные размеры плиты приняты в соответствии с технологическими требованиями изготовления виброштампованием.
Плита-складка имеет форму и размеры: длина 5,8 м, ширина 2,4 м, высота 0,3 м, толщина оболочки 20 мм, угол наклона боковых граней около 23°.
Вид арматурных элементов плиты-складки, классы стали и бетона аналогичны описанным выше для плиты-оболочки.
Рис. 1. Плита-оболочка подвесного потолка
а - опалубочный чертеж; б - деталь установки монтажной петли; в - схема армирования торцевого ребра
Рис. 2. Плитка-складка подвесного потолка
а - опалубочный чертеж; б - схема армирования
Изготовление методом скользящего виброштампования
Армоцементные конструкции панелей-перегородок шириной до 3 м плоские (рис. 3) или криволинейные, с развитыми окаймляющими ребрами, подкрепленные иногда невысокими поперечными ребрами, а также плиты-оболочки покрытий сводчатые (рис. 4) целесообразно изготавливать методом скользящего виброштампования (вибропрофилирования).
В зависимости от размеров эти конструкции изготавливают на стендовых или агрегатно-поточных технологических линиях, соответственно в неподвижных или перемещаемых формах, а формующие машины либо их рабочие органы перемещаются по направляющим форм или поста формования.
Конструкции армоцементных перегородок разработаны для применения в одноэтажных и многоэтажных промышленных зданиях.
Панели могут устанавливаться вертикально и горизонтально. При вертикальной раскладке, которая является основным решением, нижний конец панели закрепляется в полу, а верхний опирается на железобетонный или металлический прогон, прикрепляемый к колоннам или покрытию (перекрытию).
Наибольшее распространение получили ребристые одинарные панели перегородок. Разработаны перегородки шириной 1 и 1,5 м по два типоразмера для каждой ширины.
Перегородки шириной 1 м имеют размеры (рис. 3): 1-й типоразмер - общая высота 2,5 - 7,2 м, высота продольных ребер - 100 мм, высота поперечных ребер, расположенных с шагом 1,5 м, - 40 мм; 2-й типоразмер - общая высота 7,3 - 12 м, высота продольных ребер - 200 мм, поперечные ребра - такие же. Толщина полки везде 20 мм.
Перегородки шириной 1,5 м имеют размеры: 1-й типоразмер - общая высота 2,5 - 7,2 м, высота продольных ребер - 120 мм, высота поперечных треугольных ребер, расположенных с шагом 1,5 м, - 40 мм; 1-й типоразмер - общая высота 7,4 - 12 м, высота продольных ребер - 200 мм, поперечные ребра - такие же. Толщина полки везде 20 мм.
Изготовление панелей перегородок производится методом скользящего виброштампования, при котором тканая сетка полок укладывается в проектное положение в процессе формования изделий без дополнительных фиксаторов.
Для съема панелей с формы в продольных ребрах предусматриваются монтажные трубки. Для соединения панелей друг с другом по высоте в продольных ребрах предусмотрены закладные пластины, приваренные к арматурным элементам поперечных ребер.
Для армирования полки панелей применяется тканая сетка № 10-1 (ГОСТ 3826-82*); продольные ребра армируются плоскими сварными каркасами из стали класса А-III (для продольных стержней) и класса В-I (для поперечных стержней); поперечные ребра армируются отдельными стержнями из стали класса В-I.
Бетон панелей перегородок мелкозернистый группы А или Б класса В30.
Для универсальных складских сводчатых зданий сельскохозяйственного назначения пролетами 18, 21 и 24 м и стрелой подъема соответствию 0,7 и 6 м разработаны армоцементные плиты-оболочки (рис. 4). Плиты представляют собой пологую короткую цилиндрическую оболочку, наружная поверхность которой описана по дуге радиусом 14,69 м. По длинным сторонам плита обрамлена продольными ребрами постоянной высоты, по короткой - наклонными торцевыми ребрами. Тонкостенная армоцементная полка толщиной 15 мм подкреплена поперечными ребрами, расположенными с шагом 1 м. Размеры плиты-оболочки: длина 12700 мм, ширина 2980 мм, стрела подъема 1730 мм. Продольные ребра имеют трапецеидальное сечение, ширина понизу 50 мм; торцевые ребра имеют толщину 10 мм; поперечные ребра - трапецеидальные, высота их 120 мм, ширина понизу 30 мм, поверху 70 - 110 мм. Для организации водоотвода с кровли внизу предусмотрен слив.
Для армирования полки плиты оболочек применяется тканая сетка № 10-1 (ГОСТ 3826-82*); для армирования поперечных ребер - отдельные стержни из арматуры класса А-III, торцевых и продольных ребер - плоские каркасы с продольной арматурой из стали класса А-III и поперечной арматурой из стали класса В-I.
Крупноразмерные плиты-оболочки сводов покрытий формуют машиной МПП-4 - самоходным порталом с двумя рабочими органами для раздельного формования продольных ребер и армоцементной оболочки (рис. 5) со скоростью 1,3 м/мин.
Рис. 5. Схема формования армоцементных плит-оболочек сводов
1 - портал; 2 - вертикально-подвижная каретка; 3 - бункер накопитель; 4 - натяжной механизм; 5 - рулонодержатель; 6 - фиксатор армирующей сетки; 7 - вибробункер; 8 - скользящий виброштамп; 9 - тележка рабочего органа
Бетонная смесь из накопительных бункеров поступает в раздаточные, разжижается вибрированием и подается в ребра или оболочку. Постоянное расстояние между бункерами, предотвращающее расслоение смеси, поддерживается автоматической следящей системой. В продольных ребрах смесь уплотняется вибраторами, прижимаемыми и скользящими по бортам формы, в поперечных - навесными. В оболочке смесь уплотняется скользящим виброштампом (вибропрофилером) с одновременным армированием тканой проволочной сеткой. Сетка из четырех рулонов шириной по 1 м, закрепленная на самоходном портале, натягивается фрикционным механизмом и фиксируется поддерживающими ее снизу стержнями гребенки в уплотненной бетонной смеси, а в конце формования отрезается дисковой плитой. Поверхность оболочки заглаживают вибропрофилером при поднятой гребенке на повышенной скорости (до 10 м/мин).
Оптимальные параметры формования: жесткость мелкозернистой бетонной смеси 4 - 5 м, частота вибрации ребер 50 Гц, оболочки - 100 Гц, амплитуда колебаний 0,15 - 0,25 м, длительность формования до 50 мин.
На свежеотформованную поверхность оболочки наносится кровля (мастичная или рулонная) или временное изоляционное укрытие, например полиэтиленовая пленка.
Режим тепловой обработки 3 + 3 + 3 ч при максимальной температуре 85 °С.
По окончании тепловой обработки плиты-оболочки распалубливают, кровлю окрашивают в 2 слоя светозащитной краской БТ-177 или ХП-799. Плиты складируют на стеллажах с опиранием в четвертях пролета и перевозят на специально оборудованных устройствах с опиранием в восьми точках.
Изготовление плоских ребристых панелей перегородок отличается укладкой натягиваемой армирующей сетки между пониженным торцевым бортом и верхним фиксатором, а также заглаживанием плоской поверхности вращающимся валиком.
Изготовление сводчатых армоцементных конструкций послойным формованием *
* Технологию изготовления и конструкцию армоцементных сводов разработали в ЛенЗНИИЭПе (кандидаты техн. наук Б.А. Миронков, С.П. Панарин, инж. Г.М. Абраменкова).
В ЛенЗНИИЭПе накоплен опыт разработки технологии изготовления элементов волнистых сводов пролетами 12 - 40 м методом послойного формования (рис. 6).
Изготовление элементов осуществляется на нагреваемых металложелезобетонных формах-матрицах. Элементы сводов пролетами 18 м имеют длину дуги 13,5 м, ширину 2 м, стрелу подъема 1,71 м, высоту поперечного сечения волны 0,4 м. Толщина плиты элемента 20 мм, а в местах размещения стержневой арматуры толщина плиты равна 35 мм. Армирование таких элементов состоит из двух слоев тканых сеток и продольных стержней, размещенных между сетками. Конструктивная схема механизированной установки, на которой осуществляется изготовление элементов с совмещением процессов армирования элементов двумя слоями сеток и продольной стержневой арматурой, приведена на рис. 6. Установка состоит из металлоконструкций формовочного поста, формовочных тележек и тяговой лебедки для перемещения тележки.
Рис. 6. Конструктивная схема установки для послойного формирования элементов сводов
1 - рельсы формовочного поста; 2 - форма, 3 - формовочные тележки; 4 - стержневая арматура; 5 - распределительная планка
Изготовление элементов осуществляется за одни рабочий проход формовочных тележек, связанных между собой жесткими тягами. Первая тележка укладывает слой бетона, уплотняет и укладывает арматурную сетку. Такой армированный слой равен половине толщины оболочки. На этот слой укладываются арматурные стержни, пропускаемые между формующими тележками. Вторая формовочная тележка так же как первая, раскладывает слой бетонной смеси и слой арматурной сетки.
Тележки перемещаются по рельсовому пути, кривизна которого соответствует кривизне продольной нейтральной оси изделий. Съемные формы устанавливаются и фиксируются на опорах формовочного поста.
Формовочные тележки имеют одинаковую конструкцию и состоят из портала, формующего устройства и трех съемных барабанов для тканой сетки. Формующий орган оборудован высокочастотными пневматическими вибраторами с частотой 167 Гц и шлейфом - скользящей опалубкой для предохранения бетонной смеси от оплывания с наклонных поверхностей формы в процессе формования. Скорость перемещения тележек 1 м/мин. Формование армоцементного элемента осуществляется в такой последовательности:
на опоры формовочного поста устанавливается форма, смазанная и очищенная от бетона с продольными бортами, в которых зафиксированы закладные детали для крепления временных поперечных стяжек;
формовочные тележки с заполненным бетоном основными бункерами наезжают на форму и останавливаются в таком положении, при котором задняя кромка шлейфа совмещается с торцом формы;
тканые сетки, пропущенные в щель между вибробалкой и приемным бункером, закрепляются в специальном устройстве у торца формы, а приемный бункер заполняется бетонной смесью; после предварительной виброобработки смеси в течение 1 мин осуществляется формование первого слоя элемента;
при подходе второй формовочной тележки к форме обе тележки останавливаются, в направляющие ролики второй формовочной тележки заправляется продольная стержневая арматура, загнутые концы которой прикрепляются с помощью инвентарных крючков к зажимному устройству, а сами стержни укладываются на первую формовочную тележку;
продолжается формование первой тележкой до положения, при котором задняя грань шлейфа второй тележки дойдет до торца формы, после чего тележки останавливаются, тканая сетка второй тележки закрепляется, приемный бункер заполняется бетоном; после предварительного уплотнения включается лебедка и осуществляется процесс формования элемента до выхода тележек за границы формы;
форма с отформованным элементом снимается с формовочного поста и переносится краном на пост изготовления торцевых бортов (рис. 7); термообработка изделий осуществляется путем контактного нагрева на форме.
Рис. 7. Опорные узлы сводчатых зданий из армоцементных элементов
а - стык элементов в шелыге свода; б - стык элемента свода с фундаментной балкой; 1 - армоцементный элемент свода; 2 - бетонный шарнир на диафрагме; 3 - деревянный нащельник; 4 - фундаментная балка; 5 – фундамент
Технология формования элементов волнистых сводов больших пролетов (рис. 8) имеет свои особенности, заключающиеся в том, что в качестве основной продольной арматуры применяются стержни большого диаметра 16 - 20 мм, а в поперечном направлении устанавливается стержневая арматура диаметром 5 - 6 мм с шагом 150 - 200 мм.
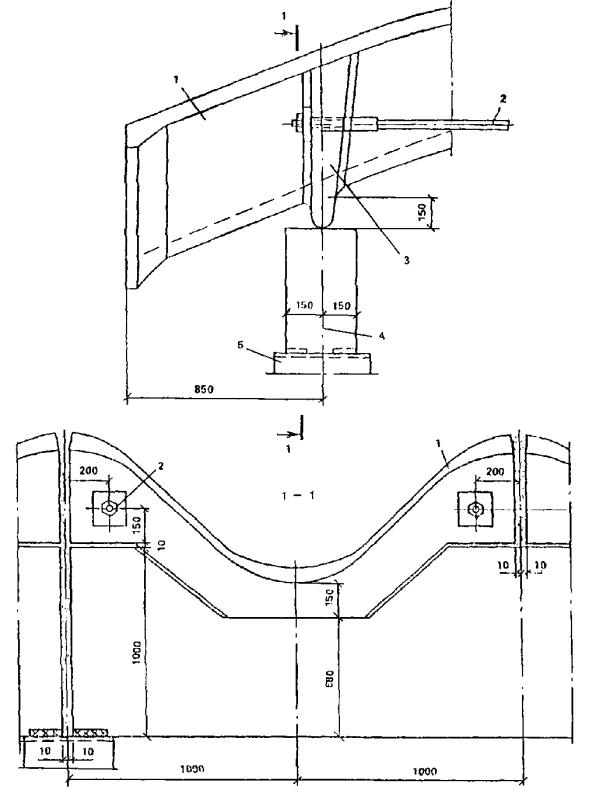
Рис. 8. Узел опирания большепролетных сводчатых покрытий из армоцементных элементов на подстропильные балки
1 - армоцементный элемент свода; 2 - металлическая затяжка; 3 - торцевая диафрагма элемента; 4 - подстропильная балка; 5 - фундамент
Часто кроме основной арматуры, располагаемой в гребнях волн, устанавливается дополнительная продольная арматура на наклонных участках сечения. Тканые сетки размещаются, как обычно, с внутренней и наружной стороны по сечению элемента. Традиционные способы изготовления, когда бетонирование осуществляется после ручной связки каркаса на форме и последующего бетонирования, не обеспечивают защитного слоя бетона и характеризуются большой трудоемкостью работ.
Элементы сборного свода пролетом 40 м имеют длину 13,9 м. В продольном направлении нейтральная ось элемента представляет дугу с радиусом 28,9 м. В поперечном сечении элемент имеет ширину 1,98 м, высоту сечения 0,5 м и стержневое армирование. Поперечная арматура состоит из 92 стержней с шагом 0,15 мм.
Изготовление элементов осуществляется способом послойного формования за два рабочих хода одной формовочной тележки в такой последовательности:
на пост устанавливается и фиксируется форма;
на ходовую раму тележки ставится формующий модуль I, предназначенный для укладки и уплотнения слоя бетона, армированного одной сеткой;
формуется первый слой, причем в процессе движения формовочной тележки с нее снимается заранее заготовленные гнутые стержни поперечной арматуры и вручную раскладываются на свежеотформованный слой бетона согласно отметкам на продольных бортах;
с ходовой рамы тележки снимается модуль I и тележка перегоняется в исходное положение;
на форму подаются стержни продольной арматуры, загибаются коротыши поперечной фиксирующей арматуры и ставятся закладные детали;
на ходовую раму тележки ставится формовочный модуль II, предназначенный для укладки и уплотнения второго слоя;
формуется последний слой элемента, армированный одним слоем тканой сетки;
форма откатывается с поста формования, в свежеотформованном изделии протыкаются отверстия диаметром 20 мм для последующего крепления затяжки, изделие укрывается пленкой и теплоизолирующим матом и проходит цикл термообработки;
на готовое изделие устанавливаются стяжки, изделие снимается с формы и укладывается на инвентарные поставки.
В случае формования утеплителя на тележку устанавливается модуль III и осуществляется его укладка за третий ход.
Снижение трудоемкости арматурных работ и отказ от вязки стержневого арматурного каркаса достигнуты путем использования простого устройства для одновременного гнутья нескольких поперечных стержней и разработки способа фиксации продольной арматуры. Фиксация 22 стержней продольной арматуры обеспечивалась приваркой вертикальных коротышек к 10 стержням поперечной арматуры (рис. 9). Поперечные стержни, уложенные равномерно на первый отформованный слой элемента, и являются основой, на которую укладываются продольные стержни. После раскладки продольной арматуры коротыши-фиксаторы загибаются.
Рис. 9. Расположение арматуры в армоцементных элементах
а - расположение стержневой арматуры в армоцементных элементах волнистых сводов; б - схема фиксации продольной арматуры; 1 - элемент свода; 2 - поперечная арматура Æ 6 А-III
По степени механизации арматурных работ и совмещения их с процессом формования элементов данная технология изготовления армоцементных сводов находится на более высоком уровне, чем технология изготовления аналогичных железобетонных элементов.
Изготовление вибролитьем структурных армоцементных плит *
* Технологию изготовления конструкции структурных армоцементных плит разработали в ЛенЗНИИЭПе (кандидаты техн. наук Б.А. Миронков, С.М. Панарин, инж. Т.С. Максим).
Изготовление вибролитьем структурных армоцементных плит по технологии ЛенЗНИИЭПа осуществляется из мелкозернистого бетона в двойные металлические формы. В настоящее время организовано производство типовых структурных армоцементных плит двух размеров: плит перекрытий с пирамидами высотой 1050 мм и размером в плане 1500 ´ 1500 мм; плит перекрытий с пирамидами высотой 900 мм и размером в плане 1500 ´ 1500 мм.
Изготовление структурных армоцементных плит осуществляется следующим образом.
В цехе организовано производство пирамидальных элементов в блоке по 4 шт. размером 3000 ´ 3000 мм (рис. 10) и армоцементных плоских плит для верхнего пояса структуры.
Изготовление армоцементных плит выполняется в стальных металлических формах по поточно-агрегатной технологии с пропариванием бетона в камерах.
Рис. 10. Схема бетонирования монтажного блока структурного покрытия
а - направления выпуска пара; б - направления перемещения конденсата
Блоки из пирамидальных элементов (ПЭ) размером 3000 ´ 3000 мм изготавливаются по поточно-агрегатной технологии с использованием двойных металлических термоформ. Форма состоит из двух частей: нижней части со стальными сердечниками для образования пирамид, паровой рубашкой и системой подачи пара в нее и верхней части - крышки для образования ребер и верхней опалубочной поверхности блока ПЭ.
На предварительно смазанную нижнюю часть надевается стальной пространственный арматурный каркас блока ПЭ, который изготавливают на специальном стенде. Затем устанавливают крышку, одновременно фиксируя арматурный каркас и закладные блока ПЭ. Верхняя крышка снабжена четырьмя загрузочными насадками для подачи пластичной мелкозернистой смеси из бадьи, оборудованной четырьмя вибраторами марки ПВ-24. Такой арматурно-опалубочный блок подается на вибростол и закрепляется на нем. Непрерывно производится заполнение полости формы и уплотнение бетона. Заполнение полости формы и уплотнение бетона производится при непрерывной подаче мелкозернистого бетона.
Масса блока ПЭ 6 т. Бетон применяют состава 1 : 3 из цемента марки 500 при модуле крупности песка 2,5 - 2,8 и жесткости смеси 10 - 20 с по малому конусу.
Изготовление складчатых армоцементных конструкций
При изготовлении армоцементных складчатых элементов широкое распространение получил прием последующего погиба элементов из свежеотформованного плоского листа (рис. 11).
Достоинство такого технологического приема заключается в простоте формования тонкого плоского армоцементного листа с использованием освоенных бетоноукладчиков, оборудованных виброкатком, и др.
В качестве формы могут применяться как металлические, так и комбинированные, бетонные формы с металлической окантовкой. Технология формования армоцементных складок методом гнутья разработана и освоена в НИИЖБ в заводских условиях.
Складчатые элементы применяют следующих размеров (рис. 12): длина до 8 м, ширина 1 - 1,5 м, толщина 15 - 25 мм. Стержневая арматура, обычная или предварительно напряженная, размещается соответственно между специально уложенными слоями тканых сеток.
Изготовление складок осуществляется по стендовой технологии на стальных листогибочных поддонах, установленных один за другим между рельсами формовочной машины. Возможно также изготовление гнутоформованных складок на агрегатно-поточной схеме.
Рис. 11. Схема изготовления складчатых армоцементных элементов с применением вибропрогиба
а - отформование плоского листа на листогибочном поддоне; б - установка вкладыша-пригруза; в - сгиб листа до складки; 1 - армоцементный лист; 2 - поворотная плоскость поддона; 3 - неподвижная плоскость поддона; 4 - поворотная плоскость вкладыша; 5 - неподвижная плоскость вкладыша; 6 - вибратор вкладыша
Для изготовления складки на очищенную и смазанную поверхность листогибочного поддона укладывается готовый арматурный пакет и натягивается продольная арматура. Армоцементная плита бетонируется при перемещении формовочной установки, оборудованной виброуплотняющим и заглаживающим устройством, вдоль форм со скоростью около 1 м/мин. Для формования плиты применяется мелкозернистая бетонная смесь состава класса В30 - 40, отношение цемента к песку около 2, водоцементное отношение В/Ц = 0,36 - 0,4, жесткость - 40 - 60 с. Фиксация сеток в проектном положении достигается их креплением к продольной, предварительно натянутой арматуре и прокладкой под арматурным пакетом поперечных стержней, извлекаемых в процессе формования. Для получения надежного сечения на поперечный изгибающий момент в месте погиба укладывается не менее четырех узких полос тканых сеток, отгибаемые борта целесообразно армировать 1 - 2 слоями тканых сеток с диагональным расположением проволок тканой сетки.
Отформованный армоцементный лист гнется с помощью бортов, которые поворачиваются домкратами по линиям сгиба.
Вибропрогиб может выполняться также с помощью шарнирного вибровкладыша (см. рис. 11), который укладывается на отформованный армоцементный лист перед погибом. Вибровкладыш должен быть утепленным, плотно уложенным на поверхность бетона. Вкладыш снимается после окончания термообработки. Рабочую поверхность вибровкладыша следует покрыть полимерным составом.
Рис. 12. Складчатая армоцементная крыша
а - фрагмент крыши жилого дома; б - фрагменты покрытия железнодорожных платформ; в - фрагмент монтажа складчатых панелей; 1 - складки; 2 – прогон
Термообработка складки после погиба ведется подачей пара во внутреннюю полость формы. Форма должна иметь сверху мягкое укрытие.
После окончания термообработки и освобождения боковых стенок изделия от формы по торцам устанавливаются временные стяжки для предохранения от возможного раскрытия боковых граней элемента (и образования трещин в месте прогиба) при съеме и транспортировке.
СОДЕРЖАНИЕ