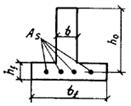
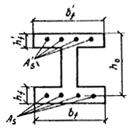
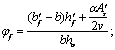|
|||||||||||||||
Все документы, представленные в каталоге, не являются их официальным изданием и предназначены исключительно для ознакомительных целей. Электронные копии этих документов могут распространяться без всяких ограничений. Вы можете размещать информацию с этого сайта на любом другом сайте.
ЦЕНТРАЛЬНЫЙ ОРДЕНА ТРУДОВОГО
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ КРАСНОГО
ЗНАМЕНИ
И ПРОЕКТНО-ЭКСПЕРИМЕНТАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ ПРОМЫШЛЕННЫХ ИНСТИТУТ БЕТОНА
ЗДАНИЙ И СООРУЖЕНИЙ И ЖЕЛЕЗОБЕТОНА
(ЦНИИпромзданий) ГОССТРОЯ СССР (НИИЖБ)
ГОССТРОЯ СССР
ПОСОБИЕ
по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов
без предварительного напряжения
арматуры
(к СНиП 2.03.01-84)
Утверждено
приказом ЦНИИпромзданий
Госстроя СССР
от 30 ноября 1984 г. № 106а
Рекомендовано к изданию решением секции несущих конструкций научно-технического совета ЦНИИпромзданий Госстроя СССР.
Содержит требования СНиП 2.03.01-84 к проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры; положения, детализирующие эти требования; приближенные способы и примеры расчета, а также рекомендации, необходимые для проектирования.
Для инженеров-проектировщиков, а также студентов строительных вузов.
Табл. 59, ил. 134.
При пользовании Пособием следует учитывать утвержденные изменения строительных норм и правил и государственных стандартов, публикуемые в журнале „Бюллетень строительной техники", „Сборнике изменений к строительным нормам и правилам" Госстроя СССР и информационном указателе „Государственные стандарты СССР" Госстандарта.
ПРЕДИСЛОВИЕ
Пособие содержит положения по проектированию бетонных и железобетонных конструкций промышленных и гражданских зданий и сооружений из тяжелых и легких бетонов, выполняемых без предварительного напряжения арматуры.
В Пособии приведены требования СНиП 2.03.01-84 к проектированию упомянутых бетонных и железобетонных конструкций; положения, детализирующие эти требования; приближенные способы расчета, а также дополнительные рекомендации, необходимые для проектирования. Номера пунктов, таблиц и приложений СНиП 2.03.01-84 указаны в скобках.
В каждом разделе Пособия даны примеры расчета элементов наиболее типичных случаев, встречающихся в практике проектирования.
Материалы для проектирования редко встречающихся ненапрягаемых конструкций (например, данные для арматуры, упрочненной вытяжкой; расчет элементов с арматурой классов A-IV, A-V и A-VI, имеющей условный предел текучести; расчет элементов на выносливость и т.п.) в настоящее Пособие не включены, а приведены в „Пособии по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов" (М., ЦИТП Госстроя СССР, 1986).
В Пособии не приведены особенности проектирования конструкций статически неопределимых и сборно-монолитных, с жесткой арматурой, а также некоторых сооружений (труб, силосов и др.), в частности не рассмотрены вопросы, связанные с определением усилий в этих конструкциях. Эти вопросы освещаются в соответствующих Пособиях и Рекомендациях.
Единицы физических величин, приведенные в Пособии, соответствуют „Перечню единиц физических величин, подлежащих применению в строительстве". При этом силы выражаются в ньютонах (Н) или в килоньютонах (кН); линейные размеры — в мм (в основном для сечений элементов) или в м (для элементов или их участков); напряжения, сопротивления, модули упругости — в мегапаскалях (МПа); распределенные нагрузки и усилия — в кН/м или Н/мм. Поскольку 1 МПа = 1 Н/мм2, при использовании в примерах расчета формул, включающих величины в МПа (напряжения, сопротивления и т. п.), остальные величины приводятся только в Н и мм (мм2).
В таблицах нормативные и расчетные сопротивления и модули упругости материалов приведены в МПа и в кгс/см2.
В Пособии использованы буквенные обозначения и индексы к ним в соответствии с СТ СЭВ 1565-79. Основные буквенные обозначения применяемых величин приведены в прил. 5. Поскольку для индексов используются только буквы латинского алфавита, соответствующие этим индексам поясняющие слова приняты не русские, а, как правило, английские. В связи с этим в прил. 5 приведены также все примененные индексы и соответствующие им русские поясняющие слова.
Пособие разработано ЦНИИпромзданий Госстроя СССР (инженеры Б.Ф. Васильев, И.К. Никитин, А.Г. Королькова; канд. техн. наук Л.Л Лемыш) и НИИЖБ Госстроя СССР (доктора техн. наук А.А. Гвоздев, Ю.П. Гуща, А.С. Залесов; кандидаты техн. наук Е.А. Чистяков, П.К. Руллэ, Н.М. Мулин, Л.Н. Зайцев, В.В. Фигаровский, Н.Г. Матков, Н.И. Катин, А.М. Фридман, Н.А. Корнев, Т.А.Кузмич) с участием НИЛ ФХММ и ТП Главмоспромстройматериалов (д-р техн. наук С.Ю. Цейтлин; кандидаты техн. наук Э.Г. Ратц, Я.М. Якобсон; инж. Е.З. Ерманок), КГБ Мосоргстройматериалов (канд. техн. наук B.C. Щукин; инженеры В.Л. Айзинсон, Е.М. Травкин, Б.И. Фельцман), ДИСИ Минвуза УССР (д-р техн. наук В.М. Баташов), Гипростроммаша Минстройдормаша СССР (инженеры Л.А. Волков, М.А. Соломович, Т.П. Заневская) и ЦНИИЭП жилища Госстроя СССР (канд. техн. наук Н.С. Стронгин; инж. Е.М. Сурманидзе).
Отзывы и замечания просим присылать по адресам:
127238, Москва, Дмитровское шоссе, 46, ЦНИИпромзданий;
109389, Москва, 2-я Институтская, 6, НИИЖБ.
1. ОБЩИЕ РЕКОМЕНДАЦИИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Рекомендации настоящего Пособия распространяются на проектирование бетонных и железобетонных конструкций, выполняемых без предварительного напряжения арматуры из тяжелого, мелкозернистого и легкого бетонов и эксплуатируемых при систематическом воздействии температур не выше 50°С и не ниже минус 70°С.
Примечания: 1. Рекомендации Пособия не распространяются на проектирование бетонных и железобетонных конструкций гидротехнических сооружений, мостов, транспортных тоннелей, труб под насыпями, покрытий автомобильных дорог и аэродромов.
2. Термины „бетоны тяжелые", „бетоны мелкозернистые" и „бетоны легкие" применяются в соответствии с ГОСТ 25192-82.
Легкие бетоны могут быть плотной и поризованной структур, поэтому в Пособии для краткости используются термины „легкий бетон" — для обозначения легких бетонов плотной структуры и „поризованный бетон" — для обозначения легких бетонов поризованной структуры с межзерновыми пустотами в уплотненной бетонной смеси свыше 6 %.
1.2. Вид легких и поризованных бетонов, а также область их применения приведены в прил. 1.
1.3. Бетонные и железобетонные конструкции зданий и сооружений, предназначенные для работы в условиях агрессивной среды и повышенной влажности, рекомендуется проектировать с учетом требований СНиП 2.03.11-85.
1.4 (1.4). Элементы сборных конструкций должны отвечать условиям механизированного изготовления на специализированных предприятиях.
Целесообразно укрупнять элементы сборных конструкций, насколько это позволяют грузоподъемность монтажных механизмов, условия изготовления и транспортирования.
1.5 (1.5). Для монолитных конструкций следует предусматривать унифицированные размеры, позволяющие применять инвентарную опалубку, а также укрупненные пространственные арматурные каркасы.
1.6 (1.6). В сборных конструкциях особое внимание должно быть обращено на прочность и долговечность соединений.
Конструкции узлов и соединений элементов должны обеспечивать с помощью различных конструктивных и технологических мероприятий надежную передачу усилий, прочность самих элементов в зоне стыка, а также связь дополнительно уложенного бетона в стыке с бетоном конструкции.
1.7 (1.7). Бетонные элементы применяются:
а) преимущественно в конструкциях, работающих на сжатие при малых эксцентриситетах продольной силы, не превышающих значений, указанных в п. 3.4;
б) в отдельных случаях в конструкциях, работающих на сжатие с большими эксцентриситетами, а также в изгибаемых конструкциях, когда их разрушение не представляет непосредственной опасности для жизни людей и сохранности оборудования (элементы, лежащие на сплошном основании, и др.).
Примечание. Конструкции рассматриваются как бетонные, если их прочность в стадии эксплуатации обеспечивается одним бетоном.
1.8 (1.8). Расчетная зимняя температура наружного воздуха принимается как средняя температура воздуха наиболее холодной пятидневки в зависимости от района строительства согласно СНиП 2.01.01.82. Расчетные технологические температуры устанавливаются заданием на проектирование.
Влажность воздуха окружающей среды определяется как средняя относительная влажность наружного воздуха наиболее жаркого месяца в зависимости от района строительства согласно СНиП 2.01.01-82 или как относительная влажность внутреннего воздуха помещений отапливаемых зданий.
1.9. Численные значения приведенных в настоящем Пособии расчетных характеристик бетона и арматуры, предельно допустимых величин ширины раскрытия трещин и прогибов применяются только при проектировании. Для оценки качества конструкций следует руководствоваться требованиями соответствующих государственных стандартов и технических условий.
ОСНОВНЫЕ РАСЧЕТНЫЕ ТРЕБОВАНИЯ
1.10 (1.10). Бетонные и железобетонные конструкции должны удовлетворять требованиям расчета по несущей способности (предельные состояния первой группы) и по пригодности к нормальной эксплуатации (предельные состояния второй группы).
а) Расчет по предельным состояниям первой группы должен обеспечивать конструкции от:
хрупкого, вязкого или иного характера разрушения (расчет по прочности с учетом в необходимых случаях прогиба конструкции перед разрушением);
потери устойчивости формы конструкции или ее положения;
усталостного разрушения (расчет на выносливость конструкций, находящихся под воздействием многократно повторяющейся нагрузки — подвижной или пульсирующей);
разрушения под совместным воздействием силовых факторов и неблагоприятных влияний внешней среды (периодического или постоянного воздействия агрессивной среды, действия попеременного замораживания и оттаивания и т. п.).
б) Расчет по предельным состояниям второй группы должен обеспечивать конструкции от:
чрезмерного раскрытия трещин (расчет по раскрытию трещин);
чрезмерных перемещений — прогибов, углов перекоса и поворота, колебаний (расчет по деформациям).
Расчет бетонных конструкций по предельным состояниям второй группы, а также на выносливость может не производиться.
Примечания: 1. Расчет на действие многократно повторяющейся нагрузки, в том числе на выносливость, выполняется в соответствии с рекомендациями „Пособия по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов" (М., ЦИТП Госстроя СССР, 1986).
2. Расчеты на устойчивость формы или положения конструкции, а также на совместное воздействие силовых факторов и неблагоприятных влияний внешней среды выполняются по соответствующим нормативным документам или Пособиям.
1.11 (1.11). Расчет по предельным состояниям конструкции в целом, а также отдельных ее элементов должен, как правило, производиться для всех стадий — изготовления, транспортирования, возведения и эксплуатации, при этом расчетные схемы должны отвечать принятым конструктивным решениям.
1.12 (1.12). Значения нагрузок и воздействий, коэффициентов «надежности по нагрузке gf, коэффициентов сочетаний, а также подразделение нагрузок на постоянные и временные должны приниматься в соответствии с требованиями СНиП 2.01.07-85.
Значения нагрузок необходимо умножать на коэффициенты надежности по назначению, принимаемые согласно „Правилам учета степени ответственности зданий и сооружений при проектировании конструкций"1 , утвержденным Госстроем СССР.
Нагрузки, учитываемые при расчете по предельным состояниям второй группы (эксплуатационные), следует принимать согласно пп. 1.15 и 1.17. При этом к длительным нагрузкам относится также часть полного значения кратковременных нагрузок, оговоренных в СНиП 2.01.07-85, а вводимую в расчет кратковременную нагрузку следует принимать уменьшенной на величину, учтенную в длительной нагрузке (например, если снеговая нагрузка для III района составляет s = 1000 Н/м2, то снеговая длительная нагрузка будет равна s = 0,3 х 1000 = 300 Н/м2, а снеговая кратковременная нагрузка — s = 1000 – 300 = 700 Н/м2).
Коэффициенты сочетаний относятся к полному значению кратковременных нагрузок.
Для не защищенных от солнечной радиации конструкций, предназначенных для работы в климатическом подрайоне IVA согласно СНиП 2.01.01-82, при расчете должны учитываться температурные климатические воздействия.
1.13 (1.13). При расчете, элементов сборных конструкций на воздействие усилий, возникающих при их подъеме, транспортировании и монтаже, нагрузку от веса элемента следует вводить с коэффициентом динамичности, равным:
при транспортировании ......... 1,60
„ подъеме и монтаже ..........1,40
В этом случае следует учитывать также коэффициент надежности по нагрузке.
1.14 (1.15). Усилия в статически неопределимых железобетонных конструкциях от нагрузок и вынужденных перемещений (вследствие изменения температуры, влажности бетона, смещения опор и т.п.), а также усилия в статически определимых конструкциях при расчете их по деформированной схеме следует, как правило, определять с учетом неупругих деформаций бетона и арматуры и наличия трещин.
1 См.: Бюллетень строительной техники, 1981, № 7.
Для конструкций, методика расчета которых с учетом неупругих свойств железобетона не разработана, а также для промежуточных стадий расчета с учетом неупругих свойств железобетона усилия в статически неопределимых конструкциях допускается определять в предположении их линейной упругости.
1.15 (1.16). Ширина непродолжительного и продолжительного раскрытия трещин для элементов, эксплуатируемых в условиях неагрессивной среды, не должна превышать величин, приведенных в табл. 1.
Элементы, указанные в поз. 1 а табл. 1, можно проектировать без предварительного напряжения лишь при специальном обосновании.
Таблица 1 (1, 2)
|
Условия работы |
Предельно допустимая ширина, мм, |
|
|
конструкций |
непродолжительного acrc1 |
продолжительного acrc2 |
|
1. Элементы, воспринимающие давление жидкостей или газов при сечении: а) полностью растянутом |
0,2 |
0,1 |
|
б) частично сжатом
|
0,3 |
0,2 |
|
2. Элементы, воспринимающие давление сыпучих тел
|
0,3 |
0,2 |
|
3. Элементы, эксплуатируемые в грунте при переменном уровне грунтовых вод
|
0,3 |
0,2 |
|
4. Прочие элементы
|
0,4 |
0.3 |
Примечание. Под непродолжительным раскрытием трещин понимается их раскрытие при совместном действии постоянных, длительных и кратковременных нагрузок, под продолжительным — только постоянных и длительных нагрузок. При этом коэффициент надежности по нагрузке принимается равным единице.
1.16 (1.19). Для железобетонных слабоармированных элементов, характеризующихся тем, что их несущая способность исчерпывается одновременно с образованием трещин в бетоне растянутой зоны, площадь сечения продольной растянутой арматуры должна быть увеличена по сравнению с требуемой из расчета по прочности не менее чем на 15 %.
Такое увеличение армирования рекомендуется производить при выполнении условия
![]()
где Mcrc — момент трещинообразоьания, определяемый согласно п. 4.2 с заменой значения Rbt,ser на 1,2 Rbt,ser;
Мu — момент, соответствующий исчерпанию несущей способности и определяемый согласно пп. 3.15—3.80; для внецентренно сжатых и растянутых элементов значения Мu определяются относительно оси, проходящей через ядровую точку, наиболее удаленную от растянутой зоны (см. п. 4.2).
Это требование может не распространяться на элементы, лежащие на сплошном основании.
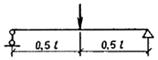
1.17 (1.20). Прогибы элементов железобетонных конструкций не должны превышать предельно допустимых значений, устанавливаемых с учетом следующих требований:
а) технологических (условия нормальной работы кранов, технологических установок, машин и т. п.);
б) конструктивных (влияние соседних элементов, ограничивающих деформации; необходимость выдерживания заданных уклонов и т. п.);
в) эстетических (впечатление людей о пригодности конструкции).
Значения предельно допустимых прогибов приведены в табл. 2.
Таблица 2 (4)
|
Элементы конструкций |
Предельно допустимые прогибы |
|
1. Подкрановые балки при кранах: ручных |
l_ 500 |
|
электрических
|
l_ 600 |
|
2. Перекрытия с плоским потолком и элементы покрытия (кроме указанных в поз. 4) при пролетах, м: l < 6 |
l_ 200 |
|
|
3 см |
|
l >7,5
|
l_ 250 |
|
3. Перекрытия с ребристым потолком и элементы лестниц при пролетах, м : l < 5 |
l_ 200 |
|
5 £ l £ 10
|
2,5 см |
|
l >10
|
400 |
|
4. Элементы покрытий сельскохозяйственных зданий производственного назначения при пролетах, м: l < 6 |
l_ 150 |
|
6 £ l £ 10
|
4 см |
|
l > 10
|
250 |
|
5. Навесные стеновые панели (при расчете из плоскости) при пролетах, м: l < 6 |
l_ 200 |
|
|
3 см |
|
l > 7,5
|
250 |
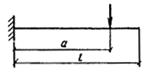
Обозначение, принятое в табл. 2: l — пролет балок или плит; для консолей принимается значение l, равное удвоенному вылету консоли.
Расчет по деформациям должен производиться при ограничении: технологическими или конструктивными требованиями — на действие постоянных, длительных и кратковременных нагрузок; эстетическими требованиями — на действие постоянных и длительных нагрузок. При этом принимается gf = 1,0.
При действии постоянных, длительных и кратковременных нагрузок прогиб балок или плит во всех случаях не должен превышать 1/150 пролета и 1/75 вылета консоли.
Значения предельно допустимых прогибов могут быть увеличены на высоту строительного подъема, если это не ограничивается технологическими или конструктивными требованиями.
Если в нижележащем помещении с гладким потолком имеются расположенные поперек пролета элемента l постоянные перегородки (не являющиеся опорами) с расстоянием между ними lp, то прогиб элемента в пределах расстояния lp (отсчитываемый от линии, соединяющей верхние точки осей перегородок) может быть допущен до 1/200 lp, при этом предельный прогиб всего элемента должен быть не более 1/500 l.
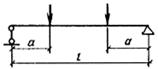
1.18 (1.20). Для не связанных с соседними элементами конструкций плит перекрытий, лестничных маршей, площадок и т. п. должна производиться дополнительная проверка по зыбкости: добавочный прогиб от кратковременно действующей сосредоточенной нагрузки 1000 Н при наиболее невыгодной схеме ее приложения должен быть не более 0,7 мм.
1.19 (1.22). Расстояния между температурно-усадочными швами, как правило, должны устанавливаться расчетом. Расчет допускается не производить, если при расчетной температуре наружного воздуха минус 40 °С и выше расстояние между температурно-усадочными швами не превышает значений, приведенных в табл. 3. Для каркасных зданий и сооружений без мостовых опорных кранов при наличии в рассматриваемом направлении связей (диафрагм жесткости) значения, указанные в табл. 3, допускается умножать на коэффициент, равный:
но не менее единицы,
где dDt — коэффициент, принимаемый равным ![]() для отапливаемых зданий и
для отапливаемых зданий и ![]() — для
неотапливаемых зданий и
сооружений (здесь Dtw, Dtc —
расчетные изменения температуры, °С,
определяемые в соответствии со СНиП 2.01.07-85, e —
относительное удлинение горизонтальных элементов от вертикальных нагрузок. Допускается принимать для железобетонных элементов e =
1 · 10–4,
для стальных e = 3 · 10–4);
— для
неотапливаемых зданий и
сооружений (здесь Dtw, Dtc —
расчетные изменения температуры, °С,
определяемые в соответствии со СНиП 2.01.07-85, e —
относительное удлинение горизонтальных элементов от вертикальных нагрузок. Допускается принимать для железобетонных элементов e =
1 · 10–4,
для стальных e = 3 · 10–4);
![]() (здесь l — длина колонны между
точками закрепления, h — высота сечения колонны в рассматриваемом направлении);
(здесь l — длина колонны между
точками закрепления, h — высота сечения колонны в рассматриваемом направлении);
![]() (здесь jext — влажность наружного воздуха, %,
в наиболее жаркий месяц года, принимаемая в соответствии
со СНиП 2.01.01-82).
(здесь jext — влажность наружного воздуха, %,
в наиболее жаркий месяц года, принимаемая в соответствии
со СНиП 2.01.01-82).
При учете коэффициента d расстояния между температурно-усадочными швами должны быть не более 150 м для отапливаемых зданий из сборных конструкций, 90 м — для отапливаемых зданий из сборно-монолитных и монолитных конструкций; для неотапливаемых зданий и сооружений указанные значения следует уменьшать на 20 %.
Таблица 3
|
Конструкции |
Наибольшие расстояния, м, между температурно-усадочными швами, допускаемые без расчета, для конструкций, находящихся |
||
|
|
внутри отапливаемых зданий или в грунте |
внутри неотапливаемых зданий |
|
|
1. Бетонные: а) сборные |
40 |
35 |
30 |
|
б) монолитные: при конструктивном армировании |
30 |
25 |
20 |
|
20 |
15 |
10 |
|
|
2. Железобетонные: а) сборно-каркасные: одноэтажные |
72 |
60 |
48 |
|
многоэтажные |
60 |
50 |
40 |
|
б) спорно-монолитные и монолитные: каркасные |
50 |
40 |
30 |
|
сплошные |
40 |
30 |
25 |
Примечание. Для железобетонных каркасных зданий (поз. 2) значения расстояния между температурно-усадочными швами определены при отсутствии связей или ори расположении связей в середине температурного блока.
1.20. При расчете перекрытая по всем предельным состояниям вес перегородок, расположенных вдоль пролета плит, учитывается следующим образом:
а) нагрузка от веса глухой жесткой перегородки (например, железобетонной сборной, выполняемой из горизонтальных элементов, железобетонной или бетонной монолитной, каменной и т. п.) прикладывается сосредоточенно на расстоянии 1/12 длины перегородки от ее краев;
б) при наличии в жесткой перегородке одного проема, целиком расположенного в пределах одной половины перегородки, нагрузка от веса меньшего простенка (включая вес половины надпроемной части перегородки) прикладывается сосредоточенно на расстоянии 1/3 ширины этого простенка от края перегородки, а нагрузка от веса остальной части перегородки — на расстоянии 1/12 длины этой части перегородки от краев проема и перегородки; при ином расположении проема нагрузка прикладывается на расстоянии 1/18 длины соответствующих частей перегородки от их краев;
в) при наличии в жесткой перегородке двух проемов и более нагрузка от веса перегородки прикладывается сосредоточенно по центрам участков, опирающихся на перекрытие;
г) для прочих перегородок 60 % их веса принимается распределенным по длине перегородки (на участках между проемами), а 40% — в виде сосредоточенных сил, приложенных в соответствии с подпунктами „а" — „в".
1.21. Распределение местной нагрузки между элементами сборных перекрытий, выполняемых из многопустотных или сплошных плит, при условии обеспечения качественной заливки швов между плитами производится с учетом рекомендаций:
а) при расчете по всем предельным состояниям принимается следующее распределение нагрузки от веса перегородок, расположенных вдоль пролета равных по ширине плит:
если перегородка расположена в пределах одной плиты, на эту плиту передается 50 % веса перегородки, а по 25 % ее веса передается на две смежные плиты;
если перегородка опирается на две соседние плиты, вес перегородки распределяется поровну между ними;
б) при расчете по предельным состояниям второй группы местные сосредоточенные нагрузки, расположенные в пределах средней трети пролета плиты, распределяются на ширину, не превышающую длины пролета; при расчете по прочности такое распределение сосредоточенных нагрузок может быть допущено лишь при условии соединения смежных плит по длине шпонками, проверяемыми расчетом (см. п. 3.115).
Примечание. Если перекрытие образовано двумя плитами, опертыми по трем сторонам, при расположении перегородки в пределах одной плиты на эту плиту передается 75 % веса перегородки; в этом случае нагрузка от веса перегородки на перекрытие передается, согласно п. 1.20, при расположении перегородки как вдоль, так и поперек плиты.
2. МАТЕРИАЛЫ ДЛЯ БЕТОННЫХ
И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
БЕТОН
2.1 (2.3). Для бетонных и железобетонных конструкций следует предусматривать бетоны следующих классов и марок:
а) классов по прочности на сжатие:
тяжелый бетон — В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30; В35; В40; В45; В50; В55; В60;
мелкозернистый бетон групп:
А — естественного твердения или подвергнутый тепловой обработке при атмосферном давлении на песке с модулем крупности свыше 2,0 — В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30; В35; В40;
Б — то же, с модулем крупности 2,0 и менее — В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30;
В — подвергнутый автоклавной обработке — В15; В20; В25; В30; В35; В40; В45; В50; В55; В60;
легкий бетон при марках по средней плотности:
D800, D900 — В2,5; В3,5; В5; В7,5*;
D1000, D1100 — В2,5; В3,5; В5; В7,5; В10; В12,5*;
D1200, D1300 — В2,5; В3,5; В5; В7,5; В10; В12,5; В15*;
D1400, D1500 — В3,5; В5; В7,5; В10; В12,5; В15; В20*; В25*; В30*;
D1600, D1700 — В5; В7,5; В10; В12,5; В15; В20; В25*; В30*; В35*;
D1800, D1900 — В10; В12,5; В15; В20; В25*; В30*; В35*; В40*;
D2000 — B20; B25; В30; В35*; В40*;
поризованный бетон при марках по средней плотности:
D800, D900, D1000, — B2,5; В3,5; В5; В7,5;
D1100, D1200, D1300
D1400 — В3,5; В5; В7,5;
б) марок по морозостойкости:
тяжелый и — F50; F75; F100; F150;
мелкозернис- F200; F300; F400; F500;
тый бетоны
легкий бетон — F25; F35; F50; F75; F100; F150; F200; F300;
поризован- — F15; F25; F35; F50;
в) марок по водонепроницаемости — W2; W4; W6; W8; W10; W12;
г) марок no средней плотности:
легкий бетон — D800; D900; D1000; D1100; D1200; D1300; D1400; D1500; D1600; D1700; D1800; D1900; D2000;
поризован- D800; D900; D1000; D1100;
ный бетон D1200; D1300; D1400.
_____________
* Данный класс легкого бетона на природных заполнителях, шлаковой пемзе и аглопорите может применяться лишь при согласовании с заводом-изготовителем.
Примечания : 1. Для конструкций, прочность на растяжение которых имеет главенствующее значение, устанавливаются классы бетона по прочности на осевое растяжение Bt согласно СНиП 2.03.01-84.
2. Термины „класс бетона" и „марка бетона" см. ГОСТ 25192-82.
3. Из поризованного бетона по настоящему Пособию могут проектироваться только внецентренно сжатые бетонные и железобетонные элементы.
2.2 (2.4). Возраст бетона, отвечающий его классу по прочности на сжатие, назначается при проектировании исходя из возможных реальных сроков загружения конструкции проектными нагрузками, способа возведения, условий твердения бетона.
При отсутствии этих данных класс бетона устанавливается в возрасте 28 сут.
Значение отпускной прочности бетона в элементах сборных конструкций следует назначать в соответствии с ГОСТ 13015.0—83 и стандартами на конструкции конкретных видов.
2.3 (2.5). Для железобетонных конструкций не допускается применять:
тяжелый и мелкозернистый бетоны класса по прочности на сжатие ниже В7,5;
для однослойных конструкций — легкий бетон класса по прочности на сжатие В2,5.
Рекомендуется принимать класс бетона по прочности на сжатие:
для железобетонных сжатых стержневых элементов — не ниже В15;
для сильнонагруженных железобетонных сжатых стержневых элементов (например, для колонн, воспринимающих значительные крановые нагрузки, и для колонн нижних этажей многоэтажных зданий) — не ниже B25;
для тонкостенных железобетонных конструкций, а также для стен зданий и сооружений, возводимых в скользящей и переставной опалубках, — не ниже В15.
Для бетонных сжатых элементов не рекомендуется применять бетон класса выше В30.
2.4 (2.8). Для замоноличивания стыков элементов сборных железобетонных конструкций класс бетона следует устанавливать в зависимости от условий работы соединяемых элементов, но принимать не ниже В7,5.
2.5 (2.9). Марки бетона по морозостойкости и водонепроницаемости бетонных и железобетонных конструкций в зависимости от режима их эксплуатации и значений расчетных зимних температур наружного воздуха в районе строительства должны приниматься:
для конструкций зданий и сооружений (кроме наружных стен отапливаемых зданий) — не ниже указанных в табл. 4;
для наружных стен отапливаемых зданий — не ниже указанных в табл. 5.
Таблица 4 (9)
|
Условия работы конструкций |
Марка бетона, не ниже |
||||||
|
|
расчетная зимняя |
||||||
|
характеристика режима |
температура наружного воздуха, °С |
для конструкций (кроме наружных стен отапливаемых зданий) зданий и сооружений класса по степени ответственности |
|||||
|
|
|
I |
II |
III |
I |
II |
III |
|
1. Попеременное замораживание и оттаивание: а) в водонасыщенном состоянии |
Ниже минус 40 |
F300 |
F200 |
F150 |
W6 |
W4 |
W2 |
|
(например, конструкции, расположенные в сезоннооттаивающем слое грунта в районах |
Ниже минус 20 до минус 40 включ. |
F200 |
F150 |
F100 |
W4 |
W2 |
Не нормируется |
|
вечной мерзлоты) |
Ниже минус 5 до минус 20 включ. |
F150 |
F100 |
F75 |
W2 |
Не нормируется |
|
|
|
Минус 5 и выше |
F100 |
F75 |
F50 |
|||
|
б) в условиях эпизодического водонасыщения (например, надземные конструкции, постоянно |
Ниже минус 40 |
F200 |
F150 |
F100 |
W4 |
W2 |
Не нормируется |
|
подвергающиеся атмосферным воздействиям) |
Ниже минус 20 до минус 40 включ. |
F100 |
F75 |
F50 |
W2 |
Не нормируется |
|
|
|
Ниже минус 5 до минус 20 включ. |
F75 |
F50 |
F35* |
Не нормируется |
||
|
|
Минус 5 и выше |
F35* |
F25* |
То же
|
|||
|
в) в условиях воздушно-влажностного состояния при отсутствии эпизодического водонасыщения |
Ниже минус 40 |
F150 |
F100 |
F75 |
W4 |
W2 |
Не нормируется |
|
(например, конструкции, постоянно подвергающиеся воздей- |
Ниже минус 20 до минус 40 включ. |
F75 |
F50 |
F35* |
|||
|
Ниже минус 5 до минус 20 включ. |
F50 |
F35* |
F25* |
То же
|
|||
|
атмосферных осадков) |
Минус 5 и выше |
F35* |
F25* |
F15** |
|
||
|
2. Возможное эпизодическое воздействие температуры ниже 0 °С: а) в водонасыщенном состоянии |
Ниже минус 40 |
F150 |
F100 |
F75 |
„ |
||
|
(например, конструкции, находящиеся в грунте или под водой) |
Ниже минус 20 до минус 40 включ. |
F75 |
F50 |
F35 |
|
||
|
|
Ниже минус 5 до минус 20 включ. |
F50 |
F35* |
F25* |
|
||
|
|
Минус 5 и выше |
F35* |
F25* |
Не нормируется |
|
||
|
б) в условиях воздушно-влажно- |
Ниже минус 40 |
F75 |
F50 |
F35* |
„ |
||
|
Ниже минус 20 до минус 40 включ. |
F50 |
F35* |
F25* |
„
|
|||
|
ваемых зданий в периоды строительства и монтажа) |
Ниже минус 5 до минус 20 включ. |
F35* |
F25* |
F15** |
|
||
|
|
Минус 5 и выше |
F25* |
F15** |
Не нормируется |
|
||
_____________
* Для тяжелого и мелкозернистого бетонов марки по морозостойкости не нормируются.
** Для тяжелого, мелкозернистого и легкого бетонов марки по морозостойкости не нормируются.
Примечания: 1. Марки бетона по морозостойкости и водонепроницаемости для конструкций сооружений водоснабжения и канализации, а также для свай и свай-оболочек следует назначать согласно требованиям соответствующих нормативных документов.
2. Расчетные зимние температуры наружного воздуха принимаются согласно указаниям п. 1.8.
Таблица 5 (10)
|
Условия работы конструкций |
Минимальная марка бетона по морозостойкости наружных стен отапливаемых зданий из бетонов |
||||||
|
относительная влажность |
расчетная зимняя температура |
||||||
|
внутреннего воздуха |
наружного воздуха, °С |
||||||
|
помещения jint, % |
|
I |
II |
III |
I |
II |
III |
|
1. jint > 75 |
Ниже минус 40 |
F100 |
F75 |
F50 |
F200 |
F150 |
F100 |
|
|
Ниже минус 20 до минус 40 включ. |
F75 |
F50 |
F35 |
F100 |
F75 |
F50 |
|
|
Ниже минус 5 до минус 20 включ. |
F50 |
F35 |
F25 |
F75 |
F50 |
Не нормируется |
|
|
Минус 5 и выше |
F35 |
F25 |
F15* |
F50 |
||
|
2. 60 < jint £ 75 |
Ниже минус 40 |
F75 |
F50 |
F35 |
F100 |
F75 |
F50 |
|
|
Ниже минус 20 до минус 40 включ. |
F50 |
F35 |
F25 |
F50 |
Не нормируется |
|
|
|
Ниже минус 5 до минус 20 включ. |
F35 |
F25 |
F15* |
He нормируется |
||
|
|
Минус 5 и выше |
F25 |
F15* |
He нормируется
|
|||
|
3. jint £ 60 |
Ниже минус 40 |
F50 |
F35 |
F25 |
F75 |
F50 |
Не нормируется |
|
|
Ниже минус 20 до минус 40 включ. |
F35 |
F25 |
F15* |
He нормируется |
||
|
|
Ниже минус 5 до минус 20 включ. |
F25 |
F15* |
He нормируется
|
|||
|
|
Минус 5 и выше |
F15* |
Не нормируется
|
||||
_____________
* Для легких бетонов марки по морозостойкости не нормируются.
Примечания: 1. При наличии паро- и гидроизоляции конструкций из тяжелых, мелкозернистых и легких бетонов их марки по морозостойкости, указанные в настоящей таблице, снижаются на одну ступень.
2. Расчетная зимняя температура наружного воздуха принимается согласно указаниям п. 1.8.
2.6 (2.10). Для замоноличивания стыков элементов сборных конструкций, которые в процессе эксплуатации или монтажа могут подвергаться воздействию отрицательных температур наружного воздуха, следует применять бетоны проектных марок по морозостойкости и водонепроницаемости не ниже принятых для стыкуемых элементов.
2.7. Для легких бетонов марки по средней плотности назначаются в соответствии с табл. 6.
Нормативные и расчетные характеристики бетона
2.8 (2.11). Нормативными сопротивлениями бетона являются сопротивление осевому сжатию призм (призменная прочность) Rbn и сопротивление осевому растяжению Rbtn.
Нормативные сопротивления бетона Rbn и Rbtn в зависимости от класса бетона В даны в табл. 7.
2.9 (2.11, 2.13). Расчетные сопротивления бетона для предельных состояний первой группы Rb и Rbt определяются путем деления нормативных сопротивлений на коэффициенты надежности по бетону, принимаемые равными: при сжатии gbc = 1,3; при растяжении gbt = 1,5.
Расчетные сопротивления бетона Rb и Rbt снижаются (или повышаются) путем умножения на коэффициенты условий работы бетона gbi, учитывающие характер действия нагрузки, условия работы конструкции, способ ее изготовления, размеры сечения и т. п.
Расчетные сопротивления бетона для предельных состояний второй группы Rb,ser и Rbt,ser принимаются равными нормативным сопротивлениям и вводятся в расчет с коэффициентом условий работы бетона gbi = 1,0.
Таблица 6
|
Класс легкого |
Марки по средней плотности для
|
||||
|
бетона по прочности на сжатие |
керамзитобетона, шунгизитобетона |
шлакопемзобетона, шлакобетона |
бетона на природных пористых заполнителях |
||
|
В2,5 |
D800-D1000 |
D100-D1400 |
D800-D900 |
D800-D1200 |
D1000-D1200 |
|
В3,5 |
D800-D1100 |
D1100-D1500 |
D900-D1300 |
D1100-D1300 |
|
|
B5 |
D800-D1200 |
D1200-D1600 |
D800-D1100 |
D1200-D1400 |
|
|
B7,5 |
D900-D1300 |
D1300-D1700 |
D900-D1200 |
D1100-D1500 |
D1300-D1500 |
|
B10 |
D1000-D1400 |
D1400-D1800 |
D1000-D1300 |
D1200-D1600 |
D1400-D1600 |
|
В12,5 |
D1000-D1400 |
D1400-D1800 |
D1000-D1400 |
D1200-D1600 |
D1400-D1600 |
|
В15 |
D1200-D1700 |
D1600-D1800 |
D1300-D1600 |
D1500-D1700 |
D1600-D1800 |
|
В20 |
D1300-D1800 |
D1700-D1900 |
D1600-D1800 |
D1700-D1900 |
|
|
B25 |
D1300-D1800 |
D1800-D1900 |
— |
D1700-D1900 |
D1700-D1900 |
|
B27,5 |
D1400-D1800 |
D1900-D2000 |
— |
D1800-D2000 |
D1800-D2000 |
|
B30 |
D1500-D1800 |
— |
— |
D1900-D2000 |
D1900-D2000 |
|
B35 |
— |
— |
— |
— |
|
|
B40 |
D1700-D1900 |
— |
— |
— |
— |
_____________
* Допускается применять при условии получения экономии цемента по сравнению с применением бетона класса B30 и неснижения других технико-экономических показателей конструкции.
Таблица 7 (12)
|
Вид сопротивления |
Бетон |
Нормативные сопротивления бетона Rbn и Rbtn и расчетные сопротивления для предельных состояний второй группы Rb,ser и Rbt,ser, МПа (кгс/см2), при классе бетона по прочности на сжатие |
|||||||
|
|
|
В2,5 |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
B15 |
B20 |
|
Сжатие осевое |
Тяжелый, |
1,9 |
2,7 |
3,5 |
5,5 |
7,5 |
9,5 |
11,0 |
15,0 |
|
(призменная прочность) Rbn и Rb,ser |
мелкозернистый и легкий |
(19,4) |
(27,5) |
(35,7) |
(56,1) |
(76,5) |
(96,9) |
(112) |
(153) |
|
Растяжение |
Тяжелый, |
0,29 |
0,39 |
0,55 |
0,70 |
0,85 |
1,00 |
1,15 |
1,40 |
|
осевое Rbtn и Rbt,ser |
мелкозернистый1 и легкий на мелком плотном заполнителе |
(2,96) |
(4,00) |
(5,61) |
(7,14) |
(8,67) |
(10,2) |
(11,7) |
(14,3) |
|
|
Легкий на |
0,29 |
0,39 |
0,55 |
0,70 |
0,85 |
1,00 |
1,10 |
1,20 |
|
|
мелком пористом заполнителе2 |
(2,96) |
(4,00) |
(5,61) |
(7,14) |
(8,67) |
(10,2) |
(11,2) |
(12,2) |
|
Сжатие осевое |
Тяжелый, |
18,5 |
22,0 |
25,5 |
29,0 |
32,0 |
36,0 |
39,5 |
43,0 |
|
(призменная прочность) Rbn и Rb,ser |
мелкозернистый и легкий |
(189) |
(224) |
(260) |
(296) |
(326) |
(367) |
(403) |
(438) |
|
Растяжение |
Тяжелый, |
1,60 |
1,80 |
1,95 |
2,10 |
2,20 |
2,30 |
2,40 |
2,50 |
|
осевое Rbtn и Rbt,ser |
мелкозернистый1 и легкий на мелком плотном заполнителе |
(16,3) |
(18,4) |
(19,9) |
(21,4) |
(22,4) |
(23,5) |
(24,5) |
(25,5) |
|
|
Легкий на мел- |
1,35 |
1,50 |
1,65 |
1,80 |
— |
— |
— |
— |
|
|
ком пористом заполнителе2 |
(13,8) |
(15,3) |
(16,8) |
(18,4) |
|
|
|
|
1 Для мелкозернистого бетона группы Б (см. п. 2.1) значения Rbtn и Rbt,ser уменьшают на 15 %.
2 Для керамзитоперлитобетона на вспученном перлитовом песке значения Rbtn и Rbt,ser уменьшают на 15 %.
Примечание. Для поризованного бетона значения Rbn и Rb,ser принимают такими же, как для легкого бетона, в значения Rbtn и Rbt,ser умножают на коэффициент 0,7.
Расчетные сопротивления бетона в зависимости от класса бетона по прочности на сжатие приведены (с округлением): для предельных состояний первой группы — в табл. 8, второй группы — в табл. 7.
В расчетные сопротивления, приведенные в табл. 8, включен коэффициент условий работы gb2, учитывающий влияние длительности действия нагрузок и условия нарастания прочности бетона во времени; порядок использования в расчете коэффициентов gb2 приведен в п. 3.1.
Расчетные сопротивления бетона, приведенные в табл. 8, в соответствующих случаях следует умножать на коэффициенты условий работы бетона согласно табл. 9.
2.10 (2.14). Значения начального модуля упругости бетона Eb при сжатии и растяжении принимаются по табл. 11.
Для бетонов, подвергающихся попеременному замораживанию и оттаиванию (см. поз. 1 табл. 4), значения Eb, указанные в табл. 11, следует умножать на коэффициент условий работы gb6, принимаемый по табл. 10.
2.11 (2.15). Коэффициент линейной температурной деформации abt при изменении температуры от минус 40 до плюс 50 °С в зависимости от вида бетона принимается равным:
для тяжелого, мелкозернистого бетонов и легкого бетона на мелком плотном заполнителе — 1·10–5 °С–1;
для легкого бетона на мелком пористом заполнителе — 0,7·10–5 °С–1;
для поризованного бетона — 0,8·10–5 °С–1.
2.12 (2.16). Начальный коэффициент поперечной деформации бетона v (коэффициент Пуассона) принимается равным 0,2 для всех видов бетона, а модуль сдвига бетона G — равным 0,4 соответствующих значений Eb, указанных в табл. 11.
2.13.
Для определения массы железобетонной или бетонной
конструкции плотность бетона принимается равной, кг/м3: для тяжелого бетона — 2400, мелкозернистого — 2200, легкого и
поризованного —марке бетона по средней плотности D, умноженной: для бетонов
класса В12,5 и выше — на 1,05, для бетонов класса В10
и ниже — 1 + w/100 (где
w — весовая влажность бетона при эксплуатации, %, определенная согласно СНиП II-3-79**;
допускается w принимать равной 10 %). При расчете конструкций в стадиях
изготовления и транспортирования плотность легких и поризованных
бетонов определяется с учетом отпускной объемной влажности w по формуле ![]() где w =
15 и 20 % соответственно
для легкого и поризованного бетонов класса В10
и ниже и w = 10 % для легких бетонов класса В12,5 и выше.
где w =
15 и 20 % соответственно
для легкого и поризованного бетонов класса В10
и ниже и w = 10 % для легких бетонов класса В12,5 и выше.
Плотность железобетона при содержании арматуры 3 % и менее может приниматься превышающей плотность бетона на 100 кг/м3; при содержании арматуры свыше 3 % плотность определяется как сумма масс бетона и арматуры на единицу объема железобетонной конструкции. При этом масса 1 м длины арматурной стали принимается по прил. 4, а масса полосовой, угловой и фасонной стали — по государственным стандартам. При определении массы наружной ограждающей конструкции из легкого бетона класса В10 и ниже следует учитывать повышенную плотность фактурных слоев.
Для определения нагрузки от собственного веса конструкции удельный вес ее, кН/м3, допускается принимать равным 0,01 плотности, кг/м3.
Таблица 8
|
Вид |
Бетон |
Коэффициент |
Расчетные сопротивления бетона для предельных состояний первой группы Rb и Rbt, МПа (кгс/см2), при классе бетона по прочности на сжатие |
|||||||||||||||
|
|
условий работы gb2 |
B2,5 |
B3,5 |
B5 |
B7,5 |
В10 |
B12,5 |
B15 |
В20 |
B25 |
В30 |
B35 |
B40 |
B45 |
B50 |
B55 |
B60 |
|
|
Тяжелый, |
0,9 |
1,3 |
1,9 |
2,5 |
4,0 |
5,4 |
6,7 |
7,7 |
10,5 |
13,0 |
15,5 |
17,5 |
20,0 |
22,5 |
25,0 |
27,0 |
29,5 |
|
|
мелкозернистый |
|
(13,3) |
(19,4) |
(25,5) |
(40,8) |
(55) |
(68,5) |
(78,5) |
(107) |
(133) |
(158) |
(178) |
(204) |
(230) |
(255) |
(275) |
(300) |
|
|
прочность) Rb |
и легкий |
1,0 |
1,5 |
2,1 |
2,8 |
4,5 |
6,0 |
7,5 |
8,5 |
11,5 |
14,5 |
17,0 |
19,5 |
22,0 |
25,0 |
27,5 |
30,0 |
33,0 |
|
|
|
|
(15,3) |
(21,4) |
(28,6) |
(45,9) |
(61,2) |
(76,5) |
(86,7) |
(117) |
(148) |
(173) |
(199) |
(224) |
(255) |
(280) |
(306) |
(336) |
|
|
|
1,1 |
1,6 |
2,3 |
3,1 |
4,9 |
6,6 |
8,2 |
9,4 |
12,5 |
16,0 |
19,0 |
21,5 |
24,0 |
27,5 |
30,5 |
33,0 |
36,5 |
|
|
|
|
(16,3) |
(23,4) |
(32,6) |
(50) |
(67,3) |
(83,5) |
(96) |
(128) |
(163) |
(194) |
(219) |
(245) |
(280) |
(310) |
(334) |
(370) |
|
Растяжение |
Тяжелый, |
0,9 |
0.18 |
0,23 |
0,33 |
0,43 |
0,51 |
0,59 |
0,67 |
0,80 |
0,95 |
1,10 |
1,15 |
1,25 |
1,30 |
1,40 |
1,45 |
1,50 |
|
осевое Rbt |
мелкозернистый1 |
|
(1,84) |
(2,34) |
(3,33) |
(4,39) |
(5,20) |
(6,01) |
(6,83) |
(8,16) |
(9,7) |
(11,2) |
(11,7) |
(12,7) |
(13,3) |
(14,3) |
(14,8) |
(15,3) |
|
|
и легкий на мел- |
1,0 |
0,20 |
0,26 |
0,37 |
0,48 |
0,57 |
0,66 |
0.75 |
0,90 |
1,05 |
1,20 |
1,30 |
1,40 |
1,45 |
1,55 |
1,60 |
1,65 |
|
|
|
(2,04) |
(2,65) |
(3,77) |
(4,89) |
(5,81) |
(6,73) |
(7,65) |
(9,18) |
(10,7) |
(12,2) |
(13,3) |
(14,3) |
(14,8) |
(15,8) |
(16,3) |
(16,8) |
|
|
|
заполнителе |
1,1 |
0,22 |
0,29 |
0,41 |
0,53 |
0,63 |
0,73 |
0,82 |
1,00 |
1,15 |
1,30 |
1,45 |
1,55 |
1,60 |
1,70 |
1,75 |
1,80 |
|
|
|
|
(2,24) |
(2,96) |
(4,18) |
(5,40) |
(6,43) |
(7,45) |
(8,36) |
(10,2) |
(11,7) |
(13,3) |
(14,8) |
(15,8) |
(16,3) |
(17,3) |
(17,8) |
(18,4) |
|
|
Легкий на мел- |
0,9 |
0,18 |
0,23 |
0,33 |
0,43 |
0,51 |
0,59 |
0,66 |
0,72 |
0,81 |
0,90 |
1,00 |
1,10 |
— |
— |
— |
— |
|
|
ком пористом |
|
(1,84) |
(2,34) |
(3,33) |
(4,39) |
(5,20) |
(6,01) |
(6,73) |
(7,34) |
(8,26) |
(9,18) |
(10,2) |
(11,2) |
|
|
|
|
|
|
заполнителе2 |
1,0 |
0,20 |
0,26 |
0,37 |
0,48 |
0,57 |
0,66 |
0,74 |
0,80 |
0,90 |
1,00 |
1,10 |
1,20 |
— |
— |
— |
— |
|
|
|
|
(2,04) |
(2,65) |
(3,77) |
(4,89) |
(5,81) |
(6,73) |
(7,55) |
(8,16) |
(9,18) |
(10,2) |
(11,2) |
(12,2) |
|
|
|
|
|
|
|
1,1 |
0,22 |
0,29 |
0,41 |
0,53 |
0,63 |
0,73 |
0,81 |
0,90 |
1,00 |
1,10 |
1,2 |
1,30 |
— |
— |
— |
— |
|
|
|
|
(2,24) |
(2,96) |
(4,18) |
(5,40) |
(6,43) |
(7,45) |
(8,26) |
(9,18) |
(10,2) |
(11,2) |
(12,2) |
(13,3) |
|
|
|
|
1 Для мелкозернистого бетона группы Б (см. п. 2.1) значения Rbt уменьшают на 15 %.
2 Для керамзитоперлитобетона на вспученном перлитовом песке значения Rbt уменьшают на 15 %.
Примечания: 1. Для поризованного бетона значения gb2 принимают такими же, как для легкого бетона, а значения Rbt умножают на коэффициент 0,7.
2. Условия применения коэффициента условий работы gb2 приведены в п. 3.1.
3. Расчетные сопротивления бетона с коэффициентом условий работы gb2 = 1,0 приняты по табл. 13 СНиП 2.03.01-84.
|
Факторы, обусловливающие введение коэффициента |
Коэффициент условий работы бетона |
|
|
условий работы |
условное обозначение |
численное значение |
|
1. Бетонирование в вертикальном положении (высота слоя бетонирования более 1,5 м) |
gb3 |
0,85* |
|
2. Бетонирование монолитных столбов и железобетонных колонн с наибольшим размером сечения менее 30 см |
gb5 |
0,85 |
|
gb6 |
См. табл. 10 |
|
|
4. Эксплуатация не защищенных от солнечной радиации конструкций в климатическом подрайоне IVA согласно СНиП 2.01.01-82 |
gb7 |
0,85 |
|
5. Бетонные конструкции |
gb9 |
0,90 |
|
6. Бетонные конструкции из тяжелого бетона класса В35 и выше либо из легкого или мелкозернистого бетона класса В25 и выше |
gb10 |
0,3 + w £ 1 (значение w — см. п. 3.14) |
|
7. Бетон для замоноличивания стыков сборных элементов при толщине шва менее 1/5 наименьшего размера сечения элемента и менее 10 см |
gb12 |
1,15 |
_____________
* Для элементов из поризованного бетона gb3 = 0,80.
Примечания: 1. Коэффициенты условий работы бетона по поз. 3—5 должны учитываться при определении расчетных сопротивлений Rb и Rbt, а по остальным позициям — только при определении Rb.
2. Коэффициенты условий работы бетона вводятся независимо друг от друга, но при этом их произведение [включая gb2 (см. п. 3.1)] должно быть не менее 0,45.
АРМАТУРА
2.14 (2.19). В качестве ненапрягаемой арматуры железобетонных конструкций (кроме указанных в п. 2.15):
следует преимущественно применять:
а) стержневую арматуру периодического профиля классов А-III и Ат-IIIC;
б) обыкновенную арматурную проволоку периодического профиля класса Вр-I в сварных сетках и каркасах;
допускается применять:
в) стержневую арматуру периодического профиля класса А-II и гладкую класса А-I для поперечной монтажной и конструктивной арматуры, а также в качестве рабочей продольной, если другие виды арматуры не могут быть использованы;
г) обыкновенную арматурную проволоку класса Вр-I — для вязаных хомутов балок высотой до 400 мм и колонн.
Таблица 10 (17)
|
Условия эксплуатации конструкции |
Расчетная зимняя температура наружного воздуха, |
Коэффициент условий работы бетона gb6 при попеременном замораживании и оттаивании для бетона |
|
|
|
°С |
тяжелого и мелкозернистого |
легкого и поризованного |
|
Попеременное замораживание |
Ниже минус 40 |
0,70 |
0,80 |
|
и оттаивание: |
Ниже минус 20 до минус 40 включ. |
0,85 |
0,90 |
|
а) в водонасыщенном состоянии (см. поз. 1а табл. |
Ниже минус 5 до минус 20 включ. |
0,90 |
1,00 |
|
4) |
Минус 5 и выше |
0,95 |
1,00 |
|
б) в условиях эпизодичес- |
Ниже минус 40 |
0,90 |
1,00 |
|
кого водонасыщения (см. поз. 1б табл. 4) |
Минус 40 и выше |
1,00 |
1,00 |
Примечания: 1. Расчетная зимняя температура наружного воздуха принимается согласно п. 1.8.
2. При превышении марки бетона по морозостойкости по сравнению с требуемой согласно табл. 4 коэффициенты настоящей таблицы могут быть увеличены на 0,05 соответственно каждой ступени превышения, однако не могут быть более единицы.
Арматуру классов A-III, Ат-IIIC, A-II и А-I рекомендуется применять в виде сварных каркасов и сварных сеток.
При обосновании экономической целесообразности допускается применять ненапрягаемую арматуру классов A-IV, A-V и A-VI и их модификаций в качестве сжатой арматуры, а класса A-IV — в качестве растянутой. Кроме того, в качестве растянутой арматуры допускается применять арматуру класса А-IIIв. Проектирование элементов с применением арматуры перечисленных классов выполняется в соответствии с „Пособием по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов" (М., ЦИТП Госстроя СССР, 1986).
В качестве конструктивной арматуры железобетонных конструкций допускается также применять обыкновенную гладкую проволоку класса В-I.
Примечания. 1. В настоящем Пособии используется термин „стержень" для обозначения арматуры любого диаметра, вида и профиля независимо от того, поставляется она в прутках или мотках (бунтах).
2. В обозначение стержневой арматуры класса А-II специального назначения добавляется буква „с" — Ас-II.
Таблица 11 (18)
|
Бетон |
Начальные модули упругости бетона Eb · 10–3, МПа (кгс/см2), при классе бетона по прочности на сжатие |
|||||||||||||||
|
|
B2,5 |
B3,5 |
B5 |
B7,5 |
B10 |
B12,5 |
B15 |
B20 |
B25 |
B30 |
B35 |
B40 |
B45 |
B50 |
B55 |
B60 |
|
Тяжелый: естественного твердения |
— |
9,5 (96,9) |
13,0 (133) |
16,0 (163) |
18,0 (184) |
21,0 (214) |
23,0 (235) |
27,0 (275) |
30,0 (306) |
32,5 (331) |
34,5 (352) |
36,0 (367) |
37,5 (382) |
39,0 (398) |
39,5 (403) |
40,0 (408) |
|
подвергнутый тепловой обработке при атмосферном давлении |
— |
8,5 (86,7) |
11,5 (117) |
14,5 (148) |
16,0 (163) |
19,0 (194) |
20,5 (209) |
24,0 (245) |
27,0 (275) |
29,0 (296) |
31,0 (316) |
32,5 (332) |
34,0 (347) |
35,0 (357) |
35,5 (362) |
36,0 (367) |
|
Мелкозернистый групп: А — естественного твердения |
— |
7,0 (71,4) |
10,0 (102) |
13,5 (138) |
15,5 (158) |
17,5 (178) |
19,5 (199) |
22,0 (224) |
24,0 (245) |
26,0 (265) |
27,5 (280) |
28,5 (291) |
— |
— |
— |
— |
|
подвергнутый тепловой обработке при атмосферном давлении |
— |
6,5 (66,3) |
9,0 (92) |
12,5 (127) |
14,0 (143) |
15,5 (158) |
17,0 (173) |
20,0 (204) |
21,5 (219) |
23,0 (235) |
24,0 (245) |
24,5 (250) |
— |
— |
— |
— |
|
Б — естественного твердения |
— |
6,5 (66,3) |
9,0 (91,8) |
12,5 (127) |
14,0 (143) |
15,5 (158) |
17,0 (173) |
20,0 (204) |
21,5 (219) |
23,0 (235) |
— |
— |
— |
— |
— |
— |
|
подвергнутый тепловой обработке при атмосферном давлении |
— |
5,5 (56,1) |
8,0 (81,6) |
11,5 (117) |
13,0 (133) |
14,5 (148) |
15,5 (158) |
17,5 (178) |
19,0 (194) |
20,5 (209) |
— |
— |
— |
— |
— |
— |
|
В — автоклавного твердения |
— |
— |
— |
— |
— |
— |
16,5 (168) |
18,0 (184) |
19,5 (199) |
21,0 (214) |
22,0 (224) |
23,0 (235) |
23,5 (240) |
24,0 (245) |
24,5 (250) |
25,0 (255) |
|
Легкий и поризованный марки по средней плотности D: 800 |
4,0 (40,8) |
4,5 (45,9) |
5,0 (51,0) |
5,5 (56,1) |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1000 |
5,0 (51,0) |
5,5 (56,1) |
6,3 (64,2) |
7,2 (73,4) |
8,0 (81,6) |
8,4 (85,7) |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1200 |
6,0 (61,2) |
6,7 (68,3) |
7,6 (77,5) |
8,7 (88,7) |
9,5 (96,9) |
10,0 (102) |
10,5 (107) |
|
|
|
|
|
|
|
|
|
|
1400 |
7,0 (71,4) |
7,8 (79,5) |
8,8 (89,7) |
10,0 (102) |
11,0 (112) |
11,7 (119) |
12,5 (127) |
13,5 (138) |
14,5 (148) |
15,5 (158) |
— |
— |
— |
— |
— |
— |
|
1600 |
— |
9,0 (91,8) |
10,0 (102) |
11,5 (117) |
12,5 (127) |
13,2 (135) |
14,0 (143) |
15,5 (158) |
16,5 (168) |
17,5 (178) |
18,0 (184) |
— |
— |
— |
— |
— |
|
1800 |
— |
— |
11,2 (114) |
13,0 (133) |
14,0 (143) |
14,7 (150) |
15,5 (158) |
17,0 (173) |
18,5 (189) |
19,5 (199) |
20,5 (209) |
21,0 (214) |
— |
— |
— |
— |
|
2000 |
— |
— |
— |
14,5 (148) |
16,0 (163) |
17,0 (173) |
18,0 (184) |
19,5 (199) |
21,0 (214) |
22,0 (224) |
23,0 (235) |
23,5 (240) |
— |
— |
— |
— |
Примечания: 1. Группы мелкозернистого бетона приведены в п. 2.1.
2. Для легкого и поризованного бетонов при промежуточных значениях марок по средней плотности начальные модули упругости принимают по линейной интерполяции.
3. Для легкого и поризованного бетонов значения Eb даны при эксплуатационной весовой влажности w, составляющей для бетона класса В12,5 и выше — 5 %, класса B10 и ниже —10 %. Если для бетонов класса B10 и ниже весовая влажность конструкций w, определенная согласно СНиП II-3-79**, существенно превышает 10 %, значения Eb при необходимости можно несколько увеличить, определяя их по табл. 11 при условной марке по средней плотности, равной D (100 + w)/110 (где D — принятая марка по средней плотности).
4. Для тяжелого бетона, подвергнутого автоклавной обработке, значения Eb, указанные в табл. 11 для бетона естественного твердения, следует умножать на коэффициент 0,75.
5. Для не защищенных от солнечной радиации конструкций, предназначенных для работы в климатическом подрайоне IVA согласно СНиП 2.01.01-82, значения Eb, указанные в табл. 11, следует умножать на коэффициент 0,85.
Таблица 12 (прил. 1)
|
|
|
|
|
Условия эксплуатации конструкции при нагрузке |
|||||||||
|
|
|
|
|
статической |
Динамической и многократно повторяющейся |
||||||||
|
Вид арматуры и документы, регламентирующие |
Класс арматуры |
Марка стали |
Диаметр арматуры, |
в отапли- |
На открытом воздухе и в неотапливаемых зданиях при расчетной температуре, °С |
в отапли- |
На открытом воздухе и в неотапливаемых зданиях при расчетной температуре, °С |
||||||
|
ее качество |
|
|
мм |
ваемых зданиях |
до минус 30 в ключ. |
ниже минус 30 до минус 40 включ. |
ниже минус 40 до минус 55 включ. |
ниже минус 55 до минус 70 включ. |
ваемых зданиях |
до минус 30 включ. |
ниже минус 30 до минус 40 включ. |
ниже минус 40 до минус 55 включ. |
ниже минус 55 до минус 70 включ. |
|
Стержневая горячекатаная |
А-I |
Ст3сп3 |
6-40 |
+ |
+ |
+ |
+ |
+1 |
+ |
+ |
– |
– |
– |
|
гладкая, ГОСТ 5781-82 и |
|
Ст3пс3 |
6-40 |
+ |
+ |
+ |
– |
– |
+ |
+ |
– |
– |
– |
|
ГОСТ 380-71 |
|
Ст3кп3 |
6-40 |
+ |
+ |
– |
– |
– |
+ |
+ |
– |
– |
– |
|
|
|
ВСт3сп2 |
6-40 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
|
ВСт3пс2 |
6-40 |
+ |
+ |
+ |
– |
– |
+ |
+ |
+ |
– |
– |
|
|
|
ВСт3кп2 |
6-40 |
+ |
+ |
– |
– |
– |
+ |
+ |
– |
– |
– |
|
|
|
ВСт3Гпс2 |
6-18 |
+ |
+ |
+ |
+ |
+1 |
+ |
+ |
+ |
+ |
+1 |
|
Стержневая горячекатаная |
А-II |
ВСт5сп2 |
10-40 |
+ |
+ |
+ |
+1 |
+1 |
+ |
+ |
+1 |
– |
– |
|
периодического профиля, |
|
ВСт5пс2 |
10-16 |
+ |
+ |
+ |
+1 |
– |
+ |
+ |
+1 |
– |
– |
|
ГОСТ 5781-82 |
|
|
18-40 |
+ |
+ |
– |
– |
– |
+ |
+1 |
– |
– |
– |
|
|
|
18Г2С |
40-80 |
+ |
+ |
+ |
+ |
+1 |
+ |
+ |
+ |
+ |
+1 |
|
|
Ас-II |
10ГТ |
10-32 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
А-III |
З5ГС |
6-40 |
+ |
+ |
+ |
+1 |
– |
+ |
+ |
+1 |
– |
– |
|
|
|
25Г2С |
6-8 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
– |
|
|
|
|
10-40 |
+ |
+ |
+ |
+ |
+1 |
+ |
+ |
+ |
+1 |
– |
|
|
|
32Г2Рпс |
6-22 |
+ |
+ |
+ |
+1 |
– |
+ |
+ |
+1 |
– |
– |
|
Стержневая термомеханически упрочненная периодического профиля, ГОСТ 10884-81 |
Ат-IIIС |
БСт5пс; БСт5сп |
10-22 |
+ |
+ |
+ |
+1 |
– |
+ |
+ |
+1 |
– |
– |
|
Обыкновенная арматурная проволока периодического профиля, ГОСТ 6727-80 |
Вр-I |
— |
3-5 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
_____________
1 Допускается применять только в вязаных каркасах и сетках.
Примечания: 1. В таблице знак „+" означает допускается, знак „–" — не допускается.
2. Расчетная температура принимается согласно указаниям п. 1.8.
3. В данной таблице нагрузки следует относить к динамическим, если доля этих нагрузок при расчете конструкций по прочности превышает 0,1 статической нагрузки; к многократно повторяющимся — нагрузки, при которых требуется расчет конструкций на выносливость.
Таблица 13 (прил. 2)
|
Характеристика |
Расчетная температура, °С |
|||
|
закладных деталей |
до минус 30 включ. |
ниже минус 30 до минус 40 включ. |
||
|
|
марка стали по ГОСТ 380-71 |
толщина проката, мм |
марка стали по ГОСТ 380-71 |
толщина проката, мм |
|
1. Рассчитываемые на усилия от нагрузок: а) статических |
ВСт3кп2 |
4-30 |
ВСт3пс6 |
4-25 |
|
б) динамических и много- |
ВСт3пс6 |
4-10 |
ВСт3пс6 |
4-10 |
|
кратно повторяющихся |
ВСт3Гпс5 |
11-30 |
ВСт3Гпс5 |
11-30 |
|
|
BCT3сп5 |
11-25 |
ВСт3сп5 |
11-25 |
|
2. Конструктивные (не рассчи- |
БСт3кп2 |
4-10 |
БСт3кп2 |
4-10 |
|
тываемые на силовые воздействия) |
ВСт3кп2 |
4-30 |
BCт3кп2 |
4-30 |
Примечания: 1. Расчетная температура принимается согласно указаниям п. 1.8.
2. При применении низколегированной стали, например, марок 10Г2С1, 09Г2С, 15ХСНД, а также при расчетной температуре ниже минус 40 °С выбор марки стали и электродов для закладных деталей следует производить как для стальных сварных конструкций в соответствии с требованиями СНиП II-23-81.
3. Расчетные сопротивления стали указанных марок принимаются согласно СНиП II-23-81.
Таблица 14 (19, 20)
|
Вид и класс арматуры |
Нормативные сопротивления растяжению Rsn и расчетные сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа (кгс/см2) |
Вид и класс арматуры |
Нормативные сопротивления растяжению Rsn и расчетные сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа (кгс/см2) |
|
Стержневая классов: А-I |
235 (2400) |
Проволочная класса Вр-I диаметром, мм: 3 |
410 (4200) |
|
А-II |
295 (3000) |
4 |
405 (4150) |
|
А-П1 и Ат-IIIC |
390 (4000) |
5 |
395 (4050) |
Таблица 15 (22, 23)
|
|
Расчетные сопротивления арматуры для предельных сопротивлений первой группы, МПа (кгс/см2) |
||
|
Вид и класс арматуры |
растяжению |
сжатию Rsc |
|
|
|
продольной Rs |
поперечной (хомутов и отогнутых стержней) Rsw |
|
|
Стержневая классов: А-I |
225 (2300) |
175 (1800) |
225 (2300) |
|
А-II |
280 (2850) |
225 (2300) |
280(2850) |
|
А-III диаметром, мм: 6-8 |
355 (3600) |
285 (2900) * |
355 (3600) |
|
10-40 |
365 (3750) |
290 (3000) * |
365 (3750) |
|
365 (3750) |
290 (3000) * |
365 (3750) |
|
|
Проволочная класса Вр-II диаметром, мм: 3 |
375 (3850) |
270 (2750); 300 (3050) ** |
375 (3850) |
|
4 |
365 (3750) |
265 (2700); 295 (3000) ** |
365 (3750) |
|
5 |
360 (3700) |
260 (2650); 290 (2950) ** |
360 (3700) |
_____________
* В сварных каркасах для хомутов из арматуры классов А-III и Ат-IIIC, диаметр которых менее 1/3 диаметра продольных стержней, значения Rsw принимаются равными 255 МПа (2600 кгс/см2).
** Для случая применения в вязаных каркасах.
2.15 (2.20). В конструкциях с ненапрягаемой арматурой, находящихся под давлением газов или жидкостей:
следует преимущественно применять
а) стержневую арматуру классов А-II и А-I;
допускается применять:
б) стержневую арматуру классов А-III и Ат-IIIC;
в) арматурную проволоку класса Вр-I.
2.16 (2.23). При выборе вида и марок стали для арматуры, устанавливаемой по расчету, а также прокатных сталей для закладных деталей должны учитываться температурные условия эксплуатации конструкций и характер их нагружения согласно табл. 12 и 13.
В климатических зонах с расчетной зимней температурой ниже минус 40 °С при проведении строительно-монтажных работ в холодное время года несущая способность в стадии возведения конструкций с арматурой, допускаемой к применению только в отапливаемых зданиях, должна быть обеспечена исходя из расчетного сопротивления арматуры с понижающим коэффициентом 0,7 и расчетной нагрузки с коэффициентом надёжности по нагрузке gf =1,0.
2.17 (2.24). Для монтажных (подъемных) петель элементов сборных железобетонных и бетонных конструкций должна применяться горячекатаная арматурная сталь класса Ас-II марки 10ГТ и класса А-I марок ВСт3сп2 и ВСт3пс2.
В случае, если возможен монтаж конструкций при расчетной зимней температуре ниже минус 40 °С, для монтажных петель не допускается применять сталь марки ВСт3пс2.
Нормативные и расчетные характеристики арматуры
2.18 (2.25). За нормативные сопротивления арматуры Rsn принимаются наименьшие контролируемые значения:
для стержневой арматуры — физического предела текучести;
для обыкновенной арматурной проволоки — напряжения, равного 0,75 временного сопротивления разрыву.
Нормативные сопротивления Rsn для основных видов ненапрягаемой арматуры приведены в табл. 14.
2.19 (2.26). Расчетные сопротивления арматуры растяжению и сжатию соответственно Rs и Rsc для предельных состояний первой группы определяются путем деления нормативных сопротивлений на коэффициенты надежности по арматуре gs принимаемые равными:
а) для стержневой арматуры классов:
А-I и А-II ........................................................ 1,05
Ат-IIIC и А-III диаметром 10-40 мм .............1,07
А-III диаметром 6-8 мм .................................1,10
б) для проволочной арматуры класса Вр-I ..... 1,10
Расчетные сопротивления арматуры растяжению для предельных состояний второй группы принимаются равными нормативным сопротивлениям.
Расчетные сопротивления арматуры растяжению и сжатию, используемые при расчете по предельным состояниям первой группы, приведены в табл. 15, а при расчете по предельным состояниям второй группы — в табл. 14.
2.20 (2.28). Расчетные сопротивления поперечной арматуры (хомутов и отогнутых стержней) Rsw снижаются по сравнению с Rs путем умножения на коэффициенты условий работы gs1 и gs2:
а) независимо от вида и класса арматуры — на коэффициент gs1 = 0,8, учитывающий неравномерность распределения напряжений в арматуре по длине рассматриваемого сечения;
б) для стержневой арматуры классов А-III и Ат-IIIC диаметром менее 1/3 диаметра продольных стержней и для проволочной арматуры класса Вр-I в сварных каркасах — на коэффициент gs2 = 0,9, учитывающий возможность хрупкого разрушения сварного соединения.
Расчетные сопротивления Rsw с учетом указанных коэффициентов условий работы gs1 и gs2 приведены в табл. 15.
Кроме того, при расположении рассматриваемого сечения в зоне анкеровки арматуры расчетные сопротивления Rs и Rsc умножаются на коэффициент условий работы gs5, учитывающий неполную анкеровку арматуры н определяемый согласно п. 3.44.
Для элементов из легкого бетона класса В7,5 и ниже расчетные сопротивления Rsw поперечной арматуры классов А-I и Вр-I умножаются на коэффициент условий работы gs7 = 0,8.
2.21 (2.30). Значения модуля упругости арматуры Еs принимаются равными для арматуры классов:
А-I и А-II ................. 210 000 МПа (2 100 000 кгс/см2)
А-III и Ат-IIIС ......... 200 000 „ (2 000 000 „ )
Вр-I ......................... 170 000 „ (1 700 000 „ )
3. РАСЧЕТ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
3.1. Для учета влияния длительности действия нагрузок на прочность бетона расчет бетонных и железобетонных элементов по прочности в общем случае производится:
а) на действие постоянных, длительных и кратковременных нагрузок, кроме нагрузок непродолжительного действия (ветровых, крановых, от транспортных средств, возникающих при изготовлении, транспортировании и возведении, и т. п.), а также на действие особых нагрузок, вызванных деформациями просадочных, набухающих, вечномерзлых и подобных грунтов; в этом случае расчетные сопротивления бетона сжатию и растяжению соответственно Rb и Rbt принимаются по табл. 8 gb2 = 0,9:
б) на действие всех нагрузок, включая нагрузки непродолжительного действия; в этом случае расчетные сопротивления бетона Rb и Rbt принимаются по табл. 8 при gb2 = 1,1*.
Если конструкция эксплуатируется в условиях, благоприятных для нарастания прочности бетона [твердение под водой, во влажном грунте или при влажности окружающего воздуха свыше 75 % (см. п. 1.8)], расчет по случаю „а" производится при gb2 = 1,0.
* Если при учете особых нагрузок, согласно указаниям соответствующих норм, вводится дополнительный коэффициент условий работы (например, при учете сейсмических нагрузок), принимается gb2 = 1,0.
Условие прочности должно удовлетворяться при расчете как по случаю „а", так и по случаю „б".
При отсутствии нагрузок непродолжительного действия, а также аварийных расчет по прочности производится только по случаю „а".
При наличии нагрузок непродолжительного действия или аварийных расчет производится только по случаю „б", если выполняется условие
![]() (1)
(1)
где FI — усилие (момент МI поперечная сила QI или продольная сила NI) от нагрузок, используемых при расчете по случаю „а"; при этом в расчете сечений, нормальных к продольной оси внецентренно нагруженных элементов, момент МI принимается относительно оси, проходящей через наиболее растянутый (или менее сжатый) стержень арматуры, а для бетонных элементов — относительно растянутой или наименее сжатой грани;
FII — усилие от нагрузок, используемых при расчете по случаю „б".
Допускается производить расчет только по случаю „б" и при невыполнении условия (1), принимая расчетные сопротивления бетона Rb и Rbt, (при gb2 = 1,0) с коэффициентом gbl = 0,9 FII/FI £ 1,1.
Для внецентренно сжатых элементов, рассчитываемых по недеформированной схеме, значения FI и FII можно определять без учета прогиба элемента.
Для конструкций, эксплуатируемых в условиях, благоприятных для нарастания прочности бетона, условие (1) приобретает вид FI < 0,9 FII, а коэффициент gbl = FII/FI.
РАСЧЕТ БЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.2 (3.1). Расчет по прочности бетонных элементов конструкций должен производиться для сечений, нормальных к их продольной оси. В зависимости от условий работы элементов они рассчитываются без учета, а также с учетом сопротивления бетона растянутой зоны.
Без учета сопротивления бетона растянутой зоны производится расчет внецентренно сжатых элементов, указанных в п. 1.7а, принимая, что достижение предельного состояния характеризуется разрушением сжатого бетона.
С учетом сопротивления бетона растянутой зоны производится расчет элементов, указанных в п. 1.7б, а также элементов, в которых не допускаются трещины по условиям эксплуатации конструкций (элементов, подвергающихся давлению воды, карнизов, парапетов и др.). При этом принимается, что достижение предельного состояния характеризуется разрушением бетона растянутой зоны (появлением трещин).
В случае, когда возможно образование наклонных трещин (например, элементы двутаврового и таврового сечений при наличии поперечных сил), должен производиться расчет бетонных элементов из условия (13).
Кроме того, должен производиться расчет элементов на местное сжатие (смятие) согласно п. 3.93.
Внецентренно сжатые элементы
3.3 (3.2, 1.21). При расчете внецентренно сжатых бетонных элементов должен приниматься во внимание случайный эксцентриситет продольного усилия еа, обусловленный не учтенными в расчете факторами. Эксцентриситет еа в любом случае принимается не менее:
1/600 длины элемента или расстояния между его сечениями, закрепленными от смещения;
1/30 высоты сечения;
10 мм (для сборных элементов при отсутствии других экспериментально обоснованных значений еа).
Для элементов статически неопределимых конструкций (например, защемленных по концам стен или столбов) значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения е0 принимается равным значению эксцентриситета, полученному из статического расчета конструкции, но не менее еа.
В элементах статически определимых конструкций эксцентриситет е0 находится как сумма эксцентриситетов — определяемого из статического расчета конструкции и случайного.
3.4 (3.3). При гибкости элементов l0/i > 14 (для прямоугольных сечений при l0/h > 4) необходимо учитывать влияние на их несущую способность прогибов в плоскости эксцентриситета продольного усилия и в нормальной к ней плоскости путем умножения значений e0 на коэффициент h (см. п.3.7). В случае расчета из плоскости эксцентриситета продольного усилия значение е0 принимается равным значению случайного эксцентриситета.
Применение внецентренно сжатых бетонных элементов (за исключением случаев, предусмотренных в п. 1.7б) не допускается при эксцентриситетах приложения продольной силы с учетом прогибов е0 h, превышающих:
а) в зависимости от сочетания нагрузок:
при основном сочетании ................................... 0,9 у
„ особом „ ................................... 0,95 у
б) в зависимости от класса бетона:
при классе В10 и выше ..................................... у – 10
„ В7,5 и ниже ..................................... у – 20
(здесь у — расстояние от центра тяжести сечения до наиболее сжатого волокна бетона, мм).
3.5 (3.4). Во внецентренно сжатых бетонных элементах в случаях, указанных в п. 5.122, необходимо предусматривать конструктивную арматуру.
3.6 (3.5). Расчет внецентренно сжатых бетонных элементов должен производиться без учета растянутого бетона из условия
![]() (2)
(2)
где Аb — площадь сжатой зоны бетона, определяемая из условия, что ее центр тяжести совпадает с точкой приложения равнодействующей внешних сил (черт. 1).
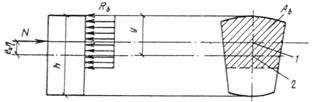
Черт. 1. Схема усилий к эпюра напряжении в поперечном
сечении внецентренно сжатого бетонного элемента без учета
сопротивления бетона растянутой зоны
1 — центр тяжести площади сжатой зоны; 2 — то же, площади всего сечения
Для элементов прямоугольного сечения Аb определяется по формуле
![]() (3)
(3)
Внецентренно сжатые бетонные элементы, в которых появление трещин не допускается по условиям эксплуатации (см. п. 3.2), независимо от расчета из условия (2) должны быть проверены с учетом сопротивления бетона растянутой зоны из условия
![]() (4)
(4)
Для элементов прямоугольного сечения условие (4) имеет вид
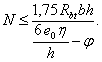 (5)
(5)
Расчет внецентренно сжатых элементов, указанных в п. 1.7б, должен производиться из условия (2) или (4).
В формулах (3) — (5):
h — коэффициент, определяемый по формуле (8);
r — расстояние от центра тяжести сечения до ядровой точки, наиболее удаленной от растянутой зоны, определяемое по формуле
![]() (6)
(6)
![]() но принимается не менее 0,7
и не более 1,0;
но принимается не менее 0,7
и не более 1,0;
sb — максимальное напряжение сжатия, вычисляемое как для упругого тела;
Wpl — момент сопротивления сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый в предположении отсутствия продольной силы по формуле
![]() (7)
(7)
где Ib0 — момент инерции площади сечения сжатой зоны бетона относительно нулевой линии;
Sb0 — статический момент площади сечения растянутой зоны бетона относительно нулевой линии;
h – х — расстояние от нулевой линии до растянутой грани, равное:
![]()
Ab1 — площадь сжатой зоны бетона, дополненная в растянутой зоне прямоугольником шириной b, равной ширине сечения по нулевой линии, и высотой h – х (черт. 2);
Sb1 — статический момент площади Аb1 относительно растянутой грани.
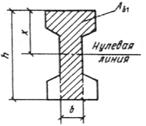
Черт. 2. К определению Ab1
Допускается значение Wpl определять по формуле
![]()
где g — см. табл. 29.
3.7 (3.6). Значение коэффициента h, учитывающего влияние прогиба на значение эксцентриситета продольного усилия e0, следует определять по формуле
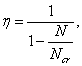 (8)
(8)
где Ncr — условная критическая сипа, определяемая по формуле
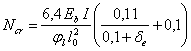 (9)
(9)
(здесь I — момент инерции бетонного сечения).
Для элементов прямоугольного сечения формула (9) имеет вид
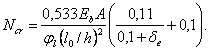 (9a)
(9a)
В формулах (9) и (9а):
jl — коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, равный:
![]() (10)
(10)
но не более 1 + b,
здесь b — коэффициент, принимаемый по табл. 16;
M1 — момент относительно растянутой или наименее сжатой грани сечения от действия постоянных, длительных и кратковременных нагрузок;
M1l — то же, от действия постоянных и длительных нагрузок;
l0 — определяется по табл. 17,
de — коэффициент, принимаемый равным e0/h, но не менее
![]()
(здесь Rb — в МПа).
Примечание. При расчете сечения по случаям „а" и „б" (см. п. 3.1) допускается значение de,min определять один раз, принимая значение Rb при gb2 = 1,0.
Таблица 16 (30)
|
Бетон |
Коэффициент b в формуле (10) |
|
1. Тяжелый |
1,0 |
|
2. Мелкозернистый групп: А |
1,3 |
|
Б |
1,5 |
|
В |
1,0 |
|
3. Легкий: при искусственных крупных заполнителях и мелком заполнителе: плотном |
1,0 |
|
пористом |
1,5 |
|
2,5 |
|
|
4. Поризованный |
2,0 |
Примечание. Группы мелкозернистого бетона приведены в п. 2.1.
Таблица 17 (31)
|
Характер опирания стен и столбов |
Расчетная длина l0 внецентренно сжатых бетонных элементов |
|
1. С опорами вверху и внизу: а) при шарнирах на двух концах независимо от величины смещения опор |
Н |
|
б) при защемлении одного из концов и возможном смещении опор для зданий: многопролетных |
1,25 Н |
|
1,50 Н |
|
|
2. Свободно стоящие |
Обозначение, принятое в табл. 17: Н — высота столба (стены) в пределах этажа за вычетом толщины плиты перекрытия или высота свободно стоящей конструкции.
3.8. Расчет с учетом прогиба внецентренно сжатых бетонных элементов прямоугольного сечения из тяжелого бетона класса не выше В20 допускается производить с помощью графика (черт. 3). При этом должно выполняться условие
![]()
где an — определяется по графику (черт. 3) в зависимости от значений е0/h и l = l0/h.
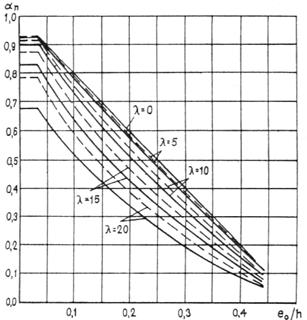
Условные обозначения:
———— при М1l /M1 = 1,0;
------------ пpи M1l /M1 = 0,5,
Черт. 3. График несущей способности внецентренно сжатых
бетонных элементов
Изгибаемые элементы
3.9 (3.8). Расчет изгибаемых бетонных элементов должен производиться из условия
![]() (11)
(11)
где Wpl — определяется по формуле (7); для элементов прямоугольного сечения Wpl принимается равным:
![]() (12)
(12)
Кроме того, для элементов таврового и двутаврового сечений должно выполняться условие
![]() (13)
(13)
где txy — касательные напряжения, определяемые как для упругого материала на уровне центра тяжести сечения.
Примеры расчета
Пример 1. Дано: межквартирная бетонная панель стены толщиной h = 200 мм, высотой Н = 2,7м, изготовленная вертикально (в кассете) из керамзитобетона на кварцевом песке-класса В15, марки по средней плотности D1600 (Еb = 14 000 МПа); полная нагрузка на 1 м стены N = 900 кН, в том числе постоянная и длительная нагрузки Nl = = 540 кН; нагрузки непродолжительного действия отсутствуют.
Требуется проверить прочность панели стены.
Расчет производим согласно п. 3.6 на действие продольной силы N = 900 кН, приложенной со случайным эксцентриситетом еа, определяемым согласно п. 3.3.
Поскольку ![]() и
и ![]() случайный
эксцентриситет принимаем равным 10 мм, т.
е. е0 = 10 мм. Закрепление панели сверху и снизу
принимаем шарнирным, следовательно, расчетная длина l0, согласно табл. 17, равна l0 = Н = 2,7 м.
случайный
эксцентриситет принимаем равным 10 мм, т.
е. е0 = 10 мм. Закрепление панели сверху и снизу
принимаем шарнирным, следовательно, расчетная длина l0, согласно табл. 17, равна l0 = Н = 2,7 м.
Так как
гибкость панели ![]() расчет производим с учетом прогиба
согласно п. 3.7.
расчет производим с учетом прогиба
согласно п. 3.7.
По формуле (10) определим коэффициент jl, принимая b = 1,0 (см. табл.
16). Поскольку эксцентриситет продольной силы не зависит от характера нагрузок, здесь можно
принять ![]()
тогда ![]()
Поскольку нагрузки непродолжительного действия отсутствуют, расчетное сопротивление бетона Rb, согласно п. 3.1, принимаем с учетом коэффициента gb2 = 0,90, т.е. Rb = 7,7 МПа, а учитывая, согласно табл. 9, коэффициенты условий работы gb3 = 0,85 и gb9 = 0,90, получим Rb = 7,7·0,85·0,90 = 5,89 МПа.
Так как 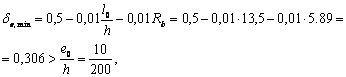
принимаем de = de,min = 0,306.
Критическую силу Ncr определим по формуле (9а), принимая площадь сечения А для 1 м длины стены, т. е. А = 200 Х 1000 = 200 000 мм2:

отсюда
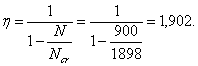
Проверим условие (2), используя формулу (3):
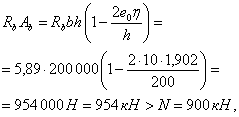
т. е. прочность панели обеспечена.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.10 (3.9). Расчет по прочности железобетонных элементов должен производиться для сечений, нормальных к их продольной оси, а также для наклонных к ней сечений наиболее опасного направления. При наличии крутящих моментов следует проверить прочность пространственных сечений, ограниченных в растянутой зоне спиральной трещиной наиболее опасного из возможных направлений. Кроме того, следует производить расчет элементов на местное действие нагрузки (смятие, продавливание, отрыв).
Изгибаемые элементы
РАСЧЕТ СЕЧЕНИЙ,
НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.11 (3.11). Расчет сечений, нормальных к продольной оси элемента, когда изгибающий момент действует в плоскости оси симметрии сечения и арматура сосредоточена у перпендикулярных указанной плоскости граней элемента, следует производить согласно пп. 3.15—3.23 в зависимости от соотношения между значением относительной высоты сжатой зоны бетона x = x/h0, определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона xR (см. п. 3.14), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs.
3.12 (3.18). Расчет изгибаемых элементов кольцевого сечения при соотношении внутреннего и наружного радиусов r1/r2 ³ 0,5 с арматурой, равномерно распределенной по длине окружности (при числе продольных стержней не менее 6), должен производиться как для внецентренно сжатых элементов согласно пп. 3.69 и 3.70, принимая значение продольной силы N = 0 и подставляя вместо Ne0 значение изгибающего момента М.
3.13.
Расчет нормальных сечений, не оговоренных в пп. 3.11, 3.12 и 3.24, производится по
формулам общего случая расчеты нормального сечения согласно п. 3.76, принимая в формуле (154) N =
0 и заменяя в условии (153) значение ![]() величиной
величиной ![]() — проекцией изгибающего
момента на плоскость, перпендикулярную прямой, ограничивающей сжатую зону.
Если ось симметрии сечения не совпадает с плоскостью действия момента или вовсе
отсутствует, положение границы сжатой зоны должно обеспечить выполнение
дополнительного условия параллельности плоскости действия моментов внешних и
внутренних сил.
— проекцией изгибающего
момента на плоскость, перпендикулярную прямой, ограничивающей сжатую зону.
Если ось симметрии сечения не совпадает с плоскостью действия момента или вовсе
отсутствует, положение границы сжатой зоны должно обеспечить выполнение
дополнительного условия параллельности плоскости действия моментов внешних и
внутренних сил.
3.14 (3.12). Значение xR определяется по формуле
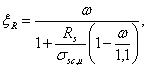 (14)
(14)
где w — характеристика сжатой зоны бетона, определяемая по формуле
![]() (15)
(15)
здесь a — коэффициент, принимаемый равным для бетона:
тяжелого ................................................. 0,85
мелкозернистого (см. п. 2.1) групп:
А ....................................................... 0,80
Б и В.................................................. 0,75
легкого и поризованного ........................0,80
ssc,u = 500 МПа — при использовании коэффициента условий работы бетона gb2 = 0,9 (см. п. 3.1);
ssc,u = 400 МПа — при использовании коэффициента gb2 =1,0 или gb2 = 1,1;
Rs, Rb — в МПа.
Значения w и xR приведены для элементов из тяжелого бетона — в табл. 18, из мелкозернистого группы А, легкого и поризованного бетонов — в табл. 19.
Таблица 18
|
Коэффициент условий |
Класс растянутой |
Обозначение |
Значения w, xR, aR и yс для элементов из тяжелого бетона классов |
||||||||||
|
работы бетона gb2 |
арматуры |
|
B12,5 |
B15 |
B20 |
B25 |
B30 |
B35 |
B40 |
B45 |
B50 |
B55 |
B60 |
|
0,9 |
Любой |
w |
0,796 |
0,788 |
0,766 |
0,746 |
0,726 |
0,710 |
0,690 |
0,670 |
0,650 |
0,634 |
0,614 |
|
|
А-III (Æ 10–40) и |
xR |
0,662 |
0,652 |
0,627 |
0,604 |
0,582 |
0,564 |
0,542 |
0,521 |
0,500 |
0,484 |
0,464 |
|
|
Bp-I (Æ 4; 5) |
aR |
0,443 |
0,440 |
0,430 |
0,422 |
0,413 |
0,405 |
0,395 |
0,381 |
0,376 |
0,367 |
0,355 |
|
|
|
yс |
4,96 |
4,82 |
4,51 |
4,26 |
4,03 |
3,86 |
3,68 |
3,50 |
3,36 |
3,23 |
3,09 |
|
|
A-II |
xR |
0,689 |
0,680 |
0,650 |
0,632 |
0,610 |
0,592 |
0,571 |
0,550 |
0,531 |
0,512 |
0,490 |
|
|
|
aR |
0,452 |
0,449 |
0,439 |
0,432 |
0,424 |
0,417 |
0,408 |
0,399 |
0,390 |
0,381 |
0,370 |
|
|
|
yс |
6,46 |
6,29 |
5,88 |
5,55 |
5,25 |
5,04 |
4,79 |
4,57 |
4,38 |
4,22 |
4,03 |
|
|
A-I |
xR |
0,708 |
0,698 |
0,674 |
0,652 |
0,630 |
0,612 |
0,591 |
0,570 |
0,551 |
0,533 |
0,510 |
|
|
|
aR |
0,457 |
0,455 |
0,447 |
0,439 |
0,432 |
0,425 |
0,416 |
0,407 |
0,399 |
0,391 |
0,380 |
|
|
|
yс |
8,04 |
7,82 |
7,32 |
6,91 |
6,54 |
6,27 |
5,96 |
5,68 |
5,46 |
5,25 |
5,01 |
|
1,0 |
Любой |
w |
0,790 |
0,782 |
0,758 |
0,734 |
0,714 |
0,694 |
0,674 |
0,650 |
0,630 |
0,610 |
0,586 |
|
|
A-III (Æ 10–40) и |
xR |
0,628 |
0,619 |
0,591 |
0,563 |
0,541 |
0,519 |
0,498 |
0,473 |
0,453 |
0,434 |
0,411 |
|
|
Bp-I (Æ 4,5) |
aR |
0,431 |
0,427 |
0,416 |
0,405 |
0,395 |
0,384 |
0,374 |
0,361 |
0,350 |
0,340 |
0,327 |
|
|
|
yс |
3,89 |
3,79 |
3,52 |
3,29 |
3,12 |
2,97 |
2,83 |
2,68 |
2,56 |
2,46 |
2,35 |
|
|
A-II |
xR |
0,660 |
0,650 |
0,623 |
0,593 |
0,573 |
0,551 |
0,530 |
0,505 |
0,485 |
0,465 |
0,442 |
|
|
|
aR |
0,442 |
0,439 |
0,429 |
0,417 |
0,409 |
0,399 |
0,390 |
0,378 |
0,367 |
0,357 |
0,344 |
|
|
|
yс |
5,07 |
4,94 |
4,60 |
4,29 |
4,07 |
3,87 |
3,69 |
3,49 |
3,34 |
3,21 |
3,06 |
|
|
A-I |
xR |
0,682 |
0,673 |
0,645 |
0,618 |
0,596 |
0,575 |
0,553 |
0,528 |
0,508 |
0,488 |
0,464 |
|
|
|
aR |
0,449 |
0,447 |
0,437 |
0,427 |
0,419 |
0,410 |
0,400 |
0,389 |
0,379 |
0,369 |
0,356 |
|
|
|
yс |
6,31 |
6,15 |
5,72 |
5,34 |
5,07 |
4,82 |
4,59 |
4,35 |
4,16 |
3,99 |
3,80 |
|
1,1 |
Любой |
w |
0,784 |
0,775 |
0,750 |
0,722 |
0,698 |
0,678 |
0,653 |
0,630 |
0,606 |
0,586 |
0,558 |
|
|
А-III (Æ 10–40) и |
xR |
0,621 |
0,610 |
0,581 |
0,550 |
0,523 |
0,502 |
0,481 |
0,453 |
0,429 |
0,411 |
0,385 |
|
|
Bp-I (Æ 4; 5) |
aR |
0,428 |
0,424 |
0,412 |
0,399 |
0,386 |
0,376 |
0,365 |
0,351 |
0,346 |
0,327 |
0,312 |
|
|
|
yс |
3,81 |
3,71 |
3,44 |
3,19 |
3,00 |
2,86 |
2,73 |
2,56 |
2,52 |
2,35 |
2,23 |
|
|
А-II |
xR |
0,650 |
0,642 |
0,613 |
0,582 |
0,556 |
0,534 |
0,514 |
0,485 |
0,477 |
0,442 |
0,417 |
|
|
|
aR |
0,439 |
0,436 |
0,425 |
0,413 |
0,401 |
0,391 |
0,382 |
0,361 |
0,363 |
0,344 |
0,330 |
|
|
|
yс |
4,97 |
4,84 |
4,49 |
4,16 |
3,91 |
3,72 |
3,53 |
3,34 |
3,29 |
3,06 |
2,91 |
|
|
A-I |
xR |
0,675 |
0,665 |
0,636 |
0,605 |
0,579 |
0,558 |
0,537 |
0,509 |
0,500 |
0,464 |
0,439 |
|
|
|
aR |
0,447 |
0,444 |
0,434 |
0,422 |
0,411 |
0,402 |
0,393 |
0,379 |
0,375 |
0,356 |
0,343 |
|
|
|
yс |
6,19 |
6,02 |
5,59 |
5,17 |
4,86 |
4,63 |
4,42 |
4,16 |
4,09 |
3,80 |
3,62 |
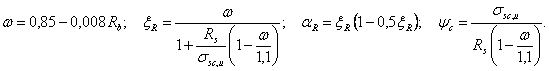
Примечание. Значения w, xR, aR и yc, приведенные в табл. 18, вычислены без учета коэффициентов gbi по табл. 9.
Таблица 19
|
Коэффициент условий |
Класс растянутой арматуры |
Обозначение |
Значения w, xR, aR и yс для элементов из мелкозернистого бетона группы А, легкого и поризованного бетонов классов |
|||||||||
|
работы бетона gb2 |
|
|
B5 |
B7,5 |
B10 |
В12,5 |
B15 |
B20 |
B25 |
В30 |
B35 |
В40 |
|
0,9 |
Любой |
w |
0,780 |
0,768 |
0,757 |
0,746 |
0,738 |
0,716 |
0,696 |
0,676 |
0,660 |
0,640 |
|
|
А-III (Æ 10–40) |
xR |
0,643 |
0,629 |
0,617 |
0,604 |
0,595 |
0,571 |
0,551 |
0.528 |
0,510 |
0,490 |
|
|
и Вр-I (Æ 4; 5) |
aR |
0,436 |
0,431 |
0,427 |
0,422 |
0,418 |
0,408 |
0,399 |
0,388 |
0,380 |
0,370 |
|
|
|
yс |
4,71 |
4,54 |
4,39 |
4,26 |
4,16 |
3,92 |
3,75 |
3,55 |
3,42 |
3,28 |
|
|
A-II |
xR |
0,671 |
0,657 |
0,644 |
0,632 |
0,623 |
0,599 |
0,577 |
0,556 |
0,539 |
0,519 |
|
|
|
aR |
0,446 |
0,441 |
0,437 |
0,432 |
0,429 |
0,420 |
0,411 |
0,401 |
0,394 |
0,384 |
|
|
|
yс |
6,14 |
5,92 |
5,73 |
5,55 |
5,43 |
5,12 |
4,86 |
4,63 |
4,46 |
4,27 |
|
|
A-I |
xR |
0,690 |
0,676 |
0,664 |
0,652 |
0,643 |
0,619 |
0,597 |
0,576 |
0,559 |
0,539 |
|
|
|
aR |
0,452 |
0,448 |
0,444 |
0,439 |
0,436 |
0,427 |
0,419 |
0,410 |
0,403 |
0,394 |
|
|
|
yс |
7,64 |
7,36 |
7,13 |
6,91 |
6,75 |
6,37 |
6,05 |
5,76 |
5,56 |
5,31 |
|
1,1 |
Любой |
w |
0,774 |
0,761 |
0,747 |
0,734 |
0,725 |
0,700 |
0,672 |
0,648 |
0,628 |
0,608 |
|
|
A-III (Æ 10–40), |
xR |
0,609 |
0,594 |
0,578 |
0,563 |
0,553 |
0,526 |
0,496 |
0,471 |
0,451 |
0,432 |
|
|
Вр-I (Æ 4; 5) |
aR |
0,424 |
0,418 |
0,411 |
0,405 |
0,400 |
0,388 |
0,373 |
0,360 |
0,349 |
0,339 |
|
|
|
yс |
3,70 |
3,56 |
3,42 |
3,29 |
3,22 |
3,01 |
2,82 |
2,67 |
2,55 |
2,45 |
|
|
А-II |
xR |
0,641 |
0,626 |
0,610 |
0,595 |
0,585 |
0,558 |
0,528 |
0,503 |
0,482 |
0,463 |
|
|
|
aR |
0,436 |
0,430 |
0,424 |
0,418 |
0,414 |
0,402 |
0,389 |
0,377 |
0,366 |
0,356 |
|
|
|
yс |
4,82 |
4,64 |
4,45 |
4,29 |
4,19 |
3,67 |
3,48 |
3,30 |
3,33 |
3,19 |
|
|
A-I |
xR |
0,663 |
0,648 |
0,633 |
0,618 |
0,608 |
0,581 |
0,551 |
0426 |
0,506 |
0,486 |
|
|
|
aR |
0,443 |
0,438 |
0,433 |
0,427 |
0,423 |
0,412 |
0,399 |
0,388 |
0,378 |
0,368 |
|
|
|
yс |
6,00 |
5,71 |
5,54 |
5,34 |
5,21 |
4,89 |
4,57 |
4,33 |
4,14 |
3,97 |
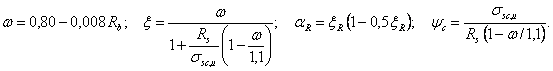
Примечание. Значения w, xR, aR и yc, приведенные в табл. 19, вычислены без учета коэффициентов gbi по табл. 9.
ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
3.15. Расчет прямоугольных сечений с арматурой, сосредоточенной у сжатой и растянутой граней элемента (черт. 4), производится следующим образом в зависимости от высоты сжатой зоны
![]() (16)
(16)
а) при ![]() — из условия
— из условия
![]() (17)
(17)
б) при x > xR — из условия
![]() (18)
(18)
где aR = xR (1 – 0,5 xR).
При этом расчетную несущую способность сечения можно несколько увеличить путем замены в условии (18) значения aR на 0,8aR + 0,2am, где при x £ 1 am = x (1 – 0,5x) или по табл. 20. Значения xR и aR определяются по табл. 18 и 19. Если х £ 0, прочность проверяется из условия
![]() (19)
(19)
Примечание. Если высота
сжатой зоны, определенная с учетом половины сжатой арматуры, ![]() расчетную несущую способность
сечения можно несколько увеличить, производя расчет по формулам (16) и (17)
без учета сжатой арматуры
расчетную несущую способность
сечения можно несколько увеличить, производя расчет по формулам (16) и (17)
без учета сжатой арматуры ![]()
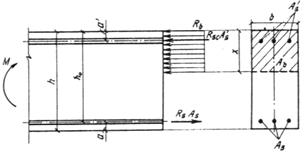
Черт. 4. Схема усилий в поперечном прямоугольном сечении
изгибаемого железобетонного элемента
3.16. Изгибаемые элементы рекомендуется проектировать так, чтобы обеспечить выполнение условия x < xR. Невыполнение этого условия можно допустить лишь в случае, когда площадь сечения растянутой арматуры определена из расчета по предельным состояниям второй группы или принята по конструктивным соображениям.
3.17. Проверка прочности прямоугольных сечений с одиночной арматурой производится:
при х < xR h0 — из условия
![]() (20)
(20)
где высота сжатой зоны равна ![]()
при х ³ xR h0 — из условия
![]() (21)
(21)
при этом расчетную несущую способность сечения можно несколько увеличить, если использовать рекомендации п. 3.15б [xR, aR — см. формулу (14) или табл. 18 и 19].
3.18. Подбор продольной арматуры производится следующим образом. Вычисляется значение
![]() (22)
(22)
Если am £ aR (см. табл. 18 и 19), сжатая арматура по расчету не требуется.
При отсутствии сжатой арматуры площадь сечения растянутой арматуры определяется по формуле
![]() (23)
(23)
где z — определяется по табл. 20 в зависимости от значения am.
Если am > aR, то требуется увеличить сечение или повысить марку бетона, или установить сжатую арматуру согласно п. 3.19.
При учете коэффициента условий работы бетона gb2 = 0,9 (см. п. 3.1) подбор растянутой арматуры можно также производить, пользуясь прил. 2.
Таблица 20
|
x |
z |
am |
x |
z |
am |
x |
z |
am |
|
0,01 |
0,995 |
0,010 |
0,26 |
0,870 |
0,226 |
0,51 |
0,745 |
0,380 |
|
0,02 |
0,990 |
0,020 |
0,27 |
0,865 |
0,234 |
0,52 |
0,740 |
0,385 |
|
0,03 |
0,985 |
0,030 |
0,28 |
0,860 |
0,241 |
0,53 |
0,735 |
0,390 |
|
0,04 |
0,980 |
0,039 |
0,29 |
0,855 |
0,243 |
0,54 |
0,730 |
0,394 |
|
0,05 |
0,975 |
0,049 |
0,30 |
0,850 |
0.255 |
0,55 |
0,725 |
0,399 |
|
0,06 |
0,970 |
0,058 |
0,31 |
0,845 |
0,262 |
0,56 |
0,720 |
0,403 |
|
0,07 |
0,965 |
0,068 |
0,32 |
0,840 |
0,269 |
0,57 |
0,715 |
0,407 |
|
0,08 |
0,960 |
0,077 |
0,33 |
0,835 |
0,276 |
0,58 |
0,710 |
0,412 |
|
0,09 |
0,955 |
0,086 |
0,34 |
0,830 |
0,282 |
0,59 |
0,705 |
0,416 |
|
0,10 |
0,950 |
0,095 |
0,35 |
0,825 |
0,289 |
0,60 |
0,700 |
0,420 |
|
0,11 |
0,945 |
0,104 |
0,36 |
0,820 |
0,295 |
0,62 |
0,690 |
0,428 |
|
0,12 |
0,940 |
0,113 |
0,37 |
0,815 |
0,302 |
0,64 |
0,680 |
0,435 |
|
0,13 |
0,935 |
0,122 |
0,38 |
0,810 |
0,308 |
0,66 |
0,670 |
0,442 |
|
0,14 |
0,930 |
0,130 |
0,39 |
0,805 |
0,314 |
0,68 |
0,660 |
0,449 |
|
0,15 |
0,925 |
0,139 |
0,40 |
0,800 |
0,320 |
0,70 |
0,650 |
0,455 |
|
0,16 |
0,920 |
0,147 |
0,41 |
0,795 |
0,326 |
0,72 |
0,640 |
0,461 |
|
0,17 |
0,915 |
0,156 |
0,42 |
0,790 |
0,332 |
0,74 |
0,630 |
0,466 |
|
0,18 |
0,910 |
0,164 |
0,43 |
0,785 |
0,338 |
0,76 |
0,620 |
0,471 |
|
0,19 |
0,905 |
0,172 |
0,44 |
0,780 |
0,343 |
0,78 |
0,610 |
0,476 |
|
0,20 |
0,900 |
0,180 |
0,45 |
0,775 |
0,349 |
0,80 |
0,600 |
0,480 |
|
0,21 |
0,895 |
0,188 |
0,46 |
0,770 |
0,354 |
0,85 |
0,575 |
0,489 |
|
0,22 |
0,890 |
0,196 |
0,47 |
0,765 |
0,360 |
0,90 |
0,550 |
0,495 |
|
0,23 |
0,885 |
0,204 |
0,48 |
0,760 |
0,365 |
0,95 |
0,525 |
0,499 |
|
0,24 |
0,880 |
0,211 |
0,49 |
0,755 |
0,370 |
1,00 |
0,500 |
0,500 |
|
0,25 |
0,875 |
0,219 |
0,50 |
0,750 |
0,375 |
— |
— |
— |
Для изгибаемых элементов прямоугольного сечения:
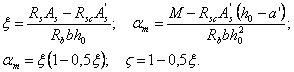
3.19.
Площади сечений растянутой Аs и сжатой ![]() арматуры,
соответствующие минимуму их суммы, для элементов из бетона класса В30 и ниже рекомендуется
определять, если по расчету требуется сжатая арматура (см. п. 3.18), по формулам:
арматуры,
соответствующие минимуму их суммы, для элементов из бетона класса В30 и ниже рекомендуется
определять, если по расчету требуется сжатая арматура (см. п. 3.18), по формулам:
![]() (24)
(24)
![]() (25)
(25)
Если значение
принятой площади сечения сжатой арматуры ![]() значительно превышает
значение, вычисленное по формуле (24),
площадь сечения растянутой арматуры определяется с учетом фактического значения
площади
значительно превышает
значение, вычисленное по формуле (24),
площадь сечения растянутой арматуры определяется с учетом фактического значения
площади ![]() по формуле
по формуле
![]() (26)
(26)
где x — определяется по табл. 20 в
зависимости от значения ![]() которое должно
удовлетворять условию
которое должно
удовлетворять условию ![]() (см. табл. 18 и 19).
(см. табл. 18 и 19).
ТАВРОВЫЕ И ДВУТАВРОВЫЕ СЕЧЕНИЯ
3.20. Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т. п.), должен производиться в зависимости от положения границы сжатой зоны:
а) если граница сжатой зоны проходит в полке (черт. 5, а), т.е. соблюдается условие
![]() (27)
(27)
расчет производится как для
прямоугольного сечения шириной ![]() в
соответствии с пп. 3.15 и 3.17;
в
соответствии с пп. 3.15 и 3.17;
б) если граница сжатой зоны проходит в ребре (черт. 5, б), т.е. условие (27) не соблюдается, расчет производится из условия
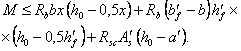 (28)
(28)
При этом высота сжатой зоны бетонах определяется по формуле
![]() (29)
(29)
и принимается не более xR h0 (см. табл. 18 и 19).
Если х ³ xR h0 , условие (28) можно записать в виде
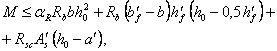 (30)
(30)
где aR — см. табл. 18 и 19.
При этом следует учитывать рекомендации п. 3.16.
Примечания: 1. При переменной высоте свесов полки
допускается принимать значение ![]() равным
средней высоте свесов.
равным
средней высоте свесов.
2. Ширина сжатой полки ![]() вводимая
в расчет, не должна превышать величин, указанных в п. 3.23.
вводимая
в расчет, не должна превышать величин, указанных в п. 3.23.
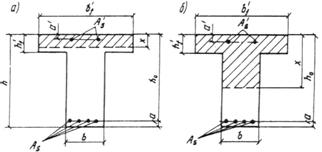
Черт. 5. Положение границы сжатой зоны в тавровом сечении
изгибаемого железобетонного элемента
а — в полке; б — в ребре
3.21. Требуемая площадь сечения сжатой арматуры определяется по формуле
![]() (31)
(31)
где aR — см. табл. 18 и 19.
3.22. Требуемая площадь сечения растянутой арматуры определяется следующим образом:
а) если граница сжатой зоны проходит в полке, т. е. соблюдается условие
![]() (32)
(32)
площадь сечения растянутой
арматуры определяется как для прямоугольного сечения шириной ![]() в соответствии с пп. 3.18 и 3.19;
в соответствии с пп. 3.18 и 3.19;
б) если граница сжатой зоны проходит в ребре, т. е. условие (32) не соблюдается, площадь сечения растянутой арматуры определяется по формуле
![]() (33)
(33)
где x определяется по табл. 20 в зависимости от значения
![]() (34)
(34)
При этом должно удовлетворяться условие am £ aR (см. табл. 18 и 19).
3.23 (3.16).
Вводимое в расчет значение ![]() принимается из
условия, что ширина свеса в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
принимается из
условия, что ширина свеса в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
а) при наличии
поперечных ребер или при ![]() расстояния в свету между продольными ребрами;
расстояния в свету между продольными ребрами;
б) при
отсутствии поперечных ребер (или при расстояниях между ними больших, чем
расстояния между продольными ребрами) и ![]()
в) при консольных свесах полки:
при ![]()
² ![]()
² ![]() — свесы не
учитываются.
— свесы не
учитываются.
ПРИМЕРЫ РАСЧЕТА
Прямоугольные сечения
Пример 2. Дано: сечение размерами b = 300 мм, h = 600 мм; a = 40 мм; gb2 = 0,9 (нагрузки непродолжительного действия отсутствуют); изгибающий момент М = 200 кН · м; бетон тяжелый класса В15 (Rb = 7,7 МПа); арматура класса A-II (Rs = 280 МПа).
Требуется определить площадь сечения продольной арматуры.
Расчет. H0 = 600 – 40 = 560 мм. Подбор продольной арматуры производим согласно п. 3.18. По формуле (22) вычислим значение am:

Из табл. 18 для элемента из бетона класса В15 с арматурой класса A-II при gb2 = 0,9 находим aR = 0,449.
Так как am = 0,276 < aR = 0,449, сжатая арматура по расчету не требуется.
Из табл. 20 при am = 0,276 находим z = 0,835.
Требуемую площадь сечения растянутой арматуры определим по формуле (23):
![]()
Принимаем 2 Æ 28 + 1 Æ 25 (As = 1598 мм2).
Пример 3. Дано: сечение размерами b = 300 мм, h = 800 мм; а = 70 мм; растянутая арматура класса A-III (Rs = 365 МПа); площадь ее сечения Аs = 2945 мм2 (6 Æ 25); gb2 = 0,9 (нагрузки непродолжительного действия отсутствуют); бетон тяжелый класса В25 (Rb = 13 МПа); изгибающий момент М = 550 кН · м.
Требуется проверить прочность сечения.
Расчет. H0 = 800 – 70 = 730 мм. Проверку прочности сечения производим согласно п. 3.17.
Определим значение х:
![]()
Из табл. 18 для элементов из бетона класса В25 с арматурой класса A-III при gb2 = 0,9 находим xR = 0,604.
Так как ![]() прочность проверим из условия (20):
прочность проверим из условия (20):

т. е. прочность сечения обеспечена.
Пример 4. Дано: сечение размерами b = 300 мм, h = 800 мм; а = 50 мм; арматура класса А-III (Rs = Rsc = 365 МПа); изгибающий момент с учетом крановой нагрузки МII = 780 кН · м; момент без учета крановой нагрузки МI = 670 кН · м; бетон тяжелый класса В15 (Rb = 8,5 МПа при gb2 = 1,0).
Требуется определить площадь сечения продольной арматуры.
Расчет производим на полную нагрузку, корректируя расчетное сопротивление бетона согласно п. 3.1.
Так как ![]() принимаем Rb = 8,5 · 1,05 = 8,93 МПа.
принимаем Rb = 8,5 · 1,05 = 8,93 МПа.
Вычислим h0 = 800 – 50 = 750 мм.
Определим требуемую площадь продольной арматуры согласно п. 3.18. По формуле (22) находим значение am:
![]()
Так как am = 0,518 > aR = 0,42 (см. табл. 18 при gb2 = 1,0), при заданных размерах сечения и классе бетона необходима сжатая арматура. Далее расчет производим согласно п. 3.19.
Принимая а' = 30 мм, по формулам (24) и (25) определим необходимую площадь сечения сжатой и растянутой арматуры:

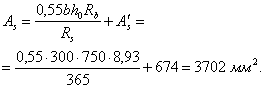
Принимаем ![]() = 763 мм2 (3 Æ 18); As = 4021 мм2 (5 Æ 32).
= 763 мм2 (3 Æ 18); As = 4021 мм2 (5 Æ 32).
Пример 5. Дано: сечение размерами b =
300 мм, h = 700 мм; а = 50 мм, а' = 30
мм; бетон тяжелый класса В30
(Rb = 15,5
МПа при gb2 = 0,9); арматура класса A-III (Rs
= 365 МПа); площадь сечения
сжатой арматуры ![]() = 942 мм2 (3 Æ 20); изгибающий момент М = 580 кН · м.
= 942 мм2 (3 Æ 20); изгибающий момент М = 580 кН · м.
Требуется определить площадь сечения растянутой арматуры.
Расчет. h0 = 700 – 50 = 650 мм. Расчет производим с учетом площади сжатой арматуры согласно п. 3.19.
Вычислим значение am:
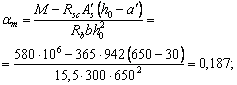
am = 0,187 < aR = 0,413 (см. табл. 18).
По табл. 20 при am = 0,187 находим x = 0,21. Необходимую площадь растянутой арматуры определим по формуле (26):
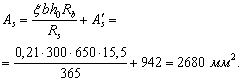
Принимаем 3 Æ 36 (Rs = 3054 мм2).
Пример 6.
Дано: сечение размерами b = 300 мм, h = 700 мм;
a = 70 мм, a’ =
30 мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9);
арматура класса A-III (Rs = Rsc = 365 МПа);
площадь сечения растянутой арматуры As = 4826 мм2
(6 Æ 32), сжатой
![]() = 339 мм2 (3 Æ 12);
изгибающий момент М = 600 кН · м.
= 339 мм2 (3 Æ 12);
изгибающий момент М = 600 кН · м.
Требуется проверить прочность сечения.
Расчет. h0 = 700 – 70 = 630 мм. Проверку прочности сечения производим согласно п. 3.15.
По формуле (16) вычислим высоту сжатой зоны х:
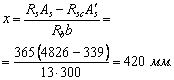
По табл. 18 находим xR = 0,604 и aR = 0,422.
Так как х = 420 мм > xR h0 = 0,604 · 630 = 380 мм, прочность сечения проверим из условия (18):
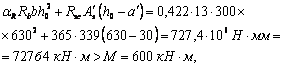
т. е. прочность сечения обеспечена.
Тавровые и двутавровые сечения
Пример 7 . Дано: сечение размерами ![]() =
1500 мм,
=
1500 мм, ![]() = 50 мм,
b = 200 мм, h =
400 мм; a = 40
мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9); арматура
класса A-III (Rs =
365 МПа); изгибающий момент М = 300 кН · м.
= 50 мм,
b = 200 мм, h =
400 мм; a = 40
мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9); арматура
класса A-III (Rs =
365 МПа); изгибающий момент М = 300 кН · м.
Требуется определить площадь сечения продольной арматуры.
Расчет. h0 = 400 – 40 = 360 мм. Расчет производим согласно п. 3.22 в предположении, что сжатая арматура по расчету не требуется.
Проверим
условие (32), принимая ![]() = 0;
= 0; ![]() = 13 · 1500 · 50 (360 – 0,5 · 50) = 326,6 · 106 Н · мм = 326,6 кН · м > М = 300 кН · м, т. е. граница сжатой зоны проходит в полке, и
расчет производим как для прямоугольного сечения шириной b =
= 13 · 1500 · 50 (360 – 0,5 · 50) = 326,6 · 106 Н · мм = 326,6 кН · м > М = 300 кН · м, т. е. граница сжатой зоны проходит в полке, и
расчет производим как для прямоугольного сечения шириной b = ![]() = 1500 мм
согласно п. 3.18. Вычислим значение am:
= 1500 мм
согласно п. 3.18. Вычислим значение am:
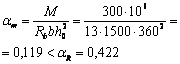 (см. табл. 18),
(см. табл. 18),
т. е. сжатая арматура действительно не требуется.
Площадь сечения растянутой арматуры вычислим по формуле (23). Для этого по табл. 20 при am = 0,1 19 находим z = 0,938, тогда
![]() мм2.
мм2.
Принимаем 4 Æ 28 (As = 2463 мм2).
Пример 8.
Дано: сечение размерами ![]() = 400
мм,
= 400
мм, ![]() =
120 мм, b = 200 мм,
h = 600 мм; a = 60
мм; бетон тяжелый класса В15 (Rb =
7,7 МПа при gb2 = 0,9); арматура
класса A-III (Rs =
365 МПа); изгибающий момент M = 270 кН · м.
=
120 мм, b = 200 мм,
h = 600 мм; a = 60
мм; бетон тяжелый класса В15 (Rb =
7,7 МПа при gb2 = 0,9); арматура
класса A-III (Rs =
365 МПа); изгибающий момент M = 270 кН · м.
Требуется определить площадь сечения растянутой арматуры.
Расчет. h0 = 600 – 60 = 540 мм. Расчет производим согласно п. 3.22 в предположении, что сжатая арматура не требуется.
Так как ![]() = 7,7 · 400 · 120 (540 – 0,5 · 120) = 177,4 · 106 Н · мм = 177,4 кН · м < М
= 270 кН · м, т. е. граница сжатой
зоны проходит в ребре, площадь сечения растянутой арматуры определим по
формуле (33).
= 7,7 · 400 · 120 (540 – 0,5 · 120) = 177,4 · 106 Н · мм = 177,4 кН · м < М
= 270 кН · м, т. е. граница сжатой
зоны проходит в ребре, площадь сечения растянутой арматуры определим по
формуле (33).
Для этого вычислим значение am:
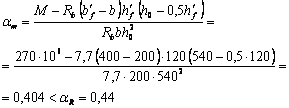
(см. табл. 18), следовательно, сжатая арматура не требуется.
Из табл. 20 при am = 0,404 находим x = 0,563, тогда
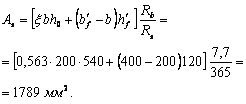
Принимаем 4 Æ 25 (As = 1964 мм2).
Пример 9. Дано: сечение размерами ![]() = 400 мм,
= 400 мм, ![]() =
100 мм, b =
200 мм, h =
600 мм; a = 70 мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9); растянутая арматура класса A-III (Rs = 365 МПа); площадь ее сечения Аs =
1964 мм2 (4 Æ 25);
=
100 мм, b =
200 мм, h =
600 мм; a = 70 мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9); растянутая арматура класса A-III (Rs = 365 МПа); площадь ее сечения Аs =
1964 мм2 (4 Æ 25); ![]() = 0;
изгибающий момент М=
300 кН · м.
= 0;
изгибающий момент М=
300 кН · м.
Требуется проверить прочность сечения.
Расчет. h0 =
600 – 70 = 530 мм. Проверку прочности сечения
производим согласно п. 3.20, принимая ![]() = 0.
Так как RsAs = 365 · 1964 = 716 860 H >
= 0.
Так как RsAs = 365 · 1964 = 716 860 H > ![]() = 13 · 400 · 100 = 520 000 H,
граница сжатой зоны проходит в ребре. Прочность сечения проверим из условия (28).
= 13 · 400 · 100 = 520 000 H,
граница сжатой зоны проходит в ребре. Прочность сечения проверим из условия (28).
Для этого по формуле (29) определим высоту сжатой зоны х:
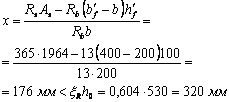
(xR найдено из табл. 18) ;
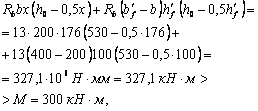
т. е. прочность сечения обеспечена.
ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ НА КОСОЙ ИЗГИБ
3.24. Расчет прямоугольных, тавровых, двутавровых и Г-образных сечений элементов, работающих на косой изгиб, допускается производить, принимая форму сжатой зоны по черт. 6, при этом должно удовлетворяться условие
где Мx — составляющая изгибающего момента в плоскости оси х (за оси х и y принимаются две взаимно перпендикулярные оси, проходящие через центр тяжести сечения растянутой арматуры параллельно сторонам сечения; для сечения с полкой ось х принимается параллельно плоскости ребра);
![]() (36)
(36)
Ab — площадь сжатой зоны бетона, равная:
![]() (37)
(37)
Аov — площадь наиболее сжатого свеса полки;
x1 — размер сжатой зоны бетона по наиболее сжатой боковой стороне сечения, определяемый по формуле
![]() (38)
(38)
b0 — расстояние от центра тяжести сечения растянутой арматуры до наиболее сжатой боковой грани ребра (стороны);
Sov,y — статический момент площади Аov в плоскости оси у относительно оси х;
Ssy — статический момент площади ![]() в плоскости оси у
относительно оси х;
в плоскости оси у
относительно оси х;
My — составляющая изгибающего момента в плоскости оси у;
Sov,x — статический момент площади Аov в плоскости оси х относительно оси у;
Ssx — статический момент площади ![]() в плоскости оси х относительно оси у.
в плоскости оси х относительно оси у.
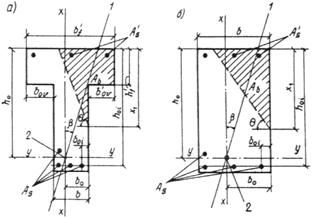
Черт. 6. Форма сжатой зоны в поперечном сечения железобетонного
элемента, работающего на косой изгиб
а — таврового сечения; б — прямоугольного сечения; 1 — плоскость действия изгибающего момента; 2 — центр тяжести сечения растянутой арматуры
Если учитываемые в расчете растянутые арматурные стержни располагаются в плоскости оси х (черт. 7), значение x1 вычисляется по формуле
![]() (39)
(39)
где 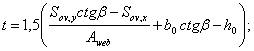
b — угол наклона плоскости действия изгибающего момента к оси х, т.е. ctgb = Мx/Мy.
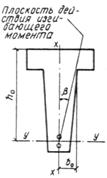
Черт. 7. Сечение с растянутыми арматурными стержнями
в плоскости оси х
Формулой (39) также следует пользоваться независимо от расположения арматуры, если необходимо определить предельное значение изгибающего момента при заданном угле b.
При расчете прямоугольных сечений значения Аov, Sov,x и Sov,y в формулах (35), (36), (38) и (39) принимаются равными нулю.
Если Ab
< Аov или x1 <
0,2![]() ,
расчет производится как для прямоугольного сечения шириной b =
,
расчет производится как для прямоугольного сечения шириной b = ![]()
Если выполняется условие
![]() (40)
(40)
(где bov — ширина наименее сжатого свеса полки), расчет производится без учета косого изгиба, т. е. по формулам пп. 3.15 и 3.20, на действие момента М = Мx, при этом следует проверить условие (41), принимая x1, как при косом изгибе.
При определении значения Ab по формуле (37) напряжение в растянутом стержне, ближайшем к границе сжатой зоны, не должно быть менее Rs, что обеспечивается соблюдением условия
![]() (41)
(41)
b0i, h0i — расстояния от рассматриваемого стержня соответственно до наиболее сжатой боковой грани ребра (стороны) и до наиболее сжатой грани, нормальной к оси х (см. черт. 6);
![]() —
ширина наиболее сжатого свеса;
—
ширина наиболее сжатого свеса;
q — угол наклона прямой, ограничивающей сжатую зону, к оси у; значение tgq определяется по формуле
![]()
Если условие (41) не соблюдается, расчет сечения производится последовательными приближениями, заменяя в формуле (37) для каждого растянутого стержня величину Rs значениями напряжений, равными:
![]() но не более Rs,
но не более Rs,
где yc, w — принимаются по табл. 18 и 19, при этом оси х и у проводятся через равнодействующую усилий в растянутых стержнях.
При проектировании конструкций не рекомендуется допускать превышения значения xi над xR более чем на 20 %, при этом допускается производить только один повторный расчет с заменой в формуле (37) значений Rs для растянутых стержней, для которых xi > xR, на напряжения, равные:
![]() (42)
(42)
При повторном расчете значение х1 определяется по формуле (39) независимо от расположения растянутых стержней.
Расчет на косой изгиб производится согласно п. 3.27, если выполняются условия:
для прямоугольных, тавровых и Г-образных сечений с полкой в сжатой зоне
![]() (43)
(43)
для двутавровых, тавровых и Г-образных сечений с полкой в растянутой зоне
![]() (44)
(44)
где hf, bov,t — высота и ширина наименее растянутого свеса полки (черт. 8).
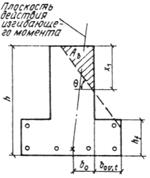
Черт. 8. Тавровое сечение со сжатой зоной,
заходящей в наименее растянутый свес полки
При
пользовании формулой (37) за растянутую
арматуру площадью Аs рекомендуется принимать арматуру, располагаемую
вблизи растянутой грани, параллельной оси у, а за сжатую арматуру площадью ![]() —
арматуру, располагаемую вблизи сжатой грани, параллельной оси у, но по одну наиболее сжатую сторону от
оси х (см. черт. 6).
—
арматуру, располагаемую вблизи сжатой грани, параллельной оси у, но по одну наиболее сжатую сторону от
оси х (см. черт. 6).
3.25. Требуемое количество растянутой арматуры при косом изгибе для элементов прямоугольного, таврового и Г-образного сечений с полкой в сжатой зоне рекомендуется определять с помощью черт. 9. Для этого ориентировочно задаются положением центра тяжести сечения растянутой арматуры и по графику определяют as в зависимости от значений:
![]()
![]()
[обозначения — см. формулы (35) — (38)].
Если amx < 0, расчет производится
как для прямоугольного сечения,
принимая ![]()
Если значение
а на графике находится по левую сторону
от кривой, отвечающей
параметру ![]() подбор арматуры
производится без учета косого изгиба, т. е. согласно пп. 3.18, 3.19 и
3.22, на действие момента М = Мx.
подбор арматуры
производится без учета косого изгиба, т. е. согласно пп. 3.18, 3.19 и
3.22, на действие момента М = Мx.
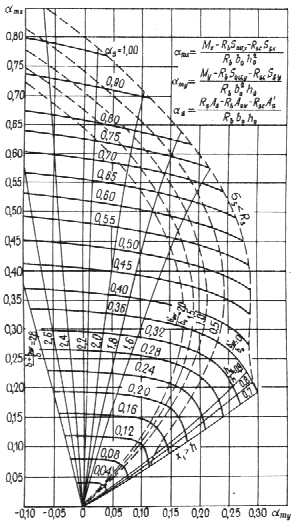
Черт. 9. График несущей способности прямоугольного, таврового
и Г-образного сечений для элементов, работающих на косой изгиб
Требуемая площадь растянутой арматуры при условии работы ее с полным расчетным сопротивлением определяется по формуле
![]() (45)
(45)
где Аov — см. формулу (36).
Центр тяжести сечения фактически принятой растянутой арматуры должен отстоять от растянутых граней не дальше, чем принятый в расчете центр тяжести. В противном случае расчет повторяют, принимая новый центр тяжести сечения растянутой арматуры.
Условием работы растянутой арматуры с полным расчетным сопротивлением является выполнение условия (41).
Для элементов
из бетона класса В25 и ниже условие (41)
всегда выполняется, если значения as на черт. 9
находятся внутри области, ограниченной осями координат и кривой, отвечающей
параметру ![]()
Если условие (41) не выполняется, следует поставить (увеличить) сжатую арматуру либо повысить класс бетона, либо увеличить размеры сечения (особенно наиболее сжатого свеса).
Значения as на графике не должны находиться между осью amy и кривой, соответствующей параметру h0/h. В противном случае x1 становится более h, и расчет тогда производится согласно п. 3.27.
3.26. Расчет на косой изгиб прямоугольных и двутавровых симметричных сечений с симметрично расположенной арматурой может производиться согласно п. 3.76, принимая N = 0.
3.27. Для не оговоренных в пп. 3.24—3.26
сечений, а также при выполнении условий (43)
и (44) или если арматура распределена по
сечению, что не позволяет до расчета установить
значения Аs
и ![]() и расположение центров тяжести
растянутой и сжатой арматуры, расчет на косой
изгиб следует производить, пользуясь формулами для общего случая расчета
нормального сечения (см. п. 3.76) с
учетом указаний п. 3.13.
и расположение центров тяжести
растянутой и сжатой арматуры, расчет на косой
изгиб следует производить, пользуясь формулами для общего случая расчета
нормального сечения (см. п. 3.76) с
учетом указаний п. 3.13.
Порядок пользования формулами общего случая рекомендуется следующий:
1) проводят две взаимно перпендикулярные оси х и у через центр тяжести сечения наиболее растянутого стержня по возможности параллельно сторонам сечения;
2) подбирают последовательными приближениями положение прямой, ограничивающей сжатую зону, так, чтобы при N = 0 удовлетворялось равенство (154) после подстановки в него значений ssi, определенных по формуле (155). При этом угол наклона этой прямой q принимают постоянным и равным углу наклона нейтральной оси, определенному как для упругого материала;
3) определяют моменты внутренних усилий относительно осей х и у соответственно Myu и Мxu.
Если оба эти момента оказываются больше или меньше соответствующих составляющих внешнего момента (My и Мx), прочность сечения считается соответственно обеспеченной или необеспеченной.
Если один из моментов (например, Мyu) меньше соответствующей составляющей внешнего момента My, а другой момент больше составляющей внешнего момента (т.е. Мxu > Мx), задаются другим углом q (большим, чем ранее принятый) и вновь производят аналогичный расчет.
Примеры расчета
Пример 10.
Дано: железобетонный прогон кровли с
уклоном 1:4 (ctgb = 4); сечение и расположение арматуры — по черт. 10; gb2 = 0,9 (нагрузки
непродолжительного действия отсутствуют); бетон тяжелый класса В25 (Rb = 13 МПа); растянутая арматура класса A-III (Rs = 365 МПа); площадь ее сечения Аs = 763 мм2
(3 Æ 18); ![]() = 0, изгибающий момент в вертикальной плоскости
М = 82,6 кН · м.
= 0, изгибающий момент в вертикальной плоскости
М = 82,6 кН · м.
Требуется проверить прочность сечения.
Расчет. Из черт. 10 следует:
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм.
мм.
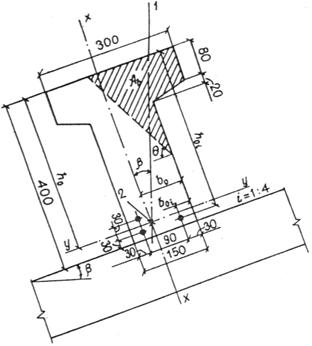
Черт. 10. К примеру расчета 10
1 — плоскость действия изгибающего момента; 2 — центр тяжести
сечения растянутой арматуры
По формуле (37) определим площадь сжатой зоны бетона Аb:
![]() мм2.
мм2.
Площадь наиболее сжатого свеса полки и статические моменты этой площади относительно осей х и у соответственно равны:
![]() мм2;
мм2;
![]() мм3;
мм3;
![]() мм3.
мм3.
Так как Аb >Аov, расчет продолжаем как для таврового сечения.
![]() мм2.
мм2.
Составляющие изгибающего момента в плоскости осей у и х соответственно равны (при ctgb = 4):
![]() кН·м.
кН·м.
![]() кН·м.
кН·м.
Определим по формуле (38) размер сжатой зоны бетона x1 по наиболее сжатой стороне сечения, принимая Ssy = 0:
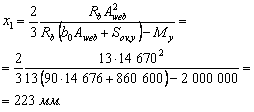
Проверим условие (40):
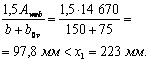
Следовательно, расчет продолжаем по формулам косого изгиба.
Проверим условие (41) для наименее растянутого стержня. Из черт. 10 имеем b0i = 30 мм, h0i = 400 – 30 = 370 мм:
![]()

(см. табл. 18).
Условие (41) не соблюдается. Расчет повторим, заменяя в формуле (37) значение Rs для наименее растянутого стержня напряжением ss, определенным по формуле (42), корректируя значения h0 и b0.
Из табл. 18 имеем w = 0,746 и yc = 4,26.
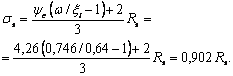
Поскольку все стержни одинакового диаметра, новые значения Аb, b0 и h0 будут равны:
![]() мм2;
мм2;
![]() мм;
мм;
![]() мм.
мм.
Аналогично определим значения Sov,y, Sov,x и Aweb:
![]()
![]()
![]()
Значение x1 определим по формуле (39):

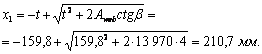
Проверим прочность сечения из условия (35), принимая Ssx = 0:

т. е. прочность сечения обеспечена.
Пример 11. По данным примера 10 необходимо подобрать площадь растянутой арматуры при моменте в вертикальной плоскости М = 64 кН·м.
Расчет. Составляющие изгибающего момента в плоскости осей у и х равны:

![]()
Определим необходимое количество арматуры согласно п. 3.25.
Принимая значения b0,
h0, S0v,x, S0v,y, Ssy = ![]() = 0 из
примера 10, находим значение amx и
amy:
= 0 из
примера 10, находим значение amx и
amy:
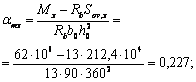
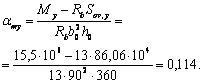
Так как amx > 0, расчет продолжаем как для таврового сечения.
Поскольку точка с координатами amx = 0,227 и amy = 0,114 на черт. 9 находится
по правую сторону от кривой, отвечающей параметру ![]() и по левую
сторону от кривой, отвечающей
параметру
и по левую
сторону от кривой, отвечающей
параметру ![]() арматура будет работать с полным расчетным сопротивлением,
т. е. условие (41) выполнено. Требуемую
площадь растянутой арматуры определим по формуле (45).
арматура будет работать с полным расчетным сопротивлением,
т. е. условие (41) выполнено. Требуемую
площадь растянутой арматуры определим по формуле (45).
По черт. 9 при amx = 0,227
и amy =
0,114 находим as = 0,25. Тогда, принимая ![]() = 0,
имеем
= 0,
имеем
![]() мм2.
мм2.
Принимаем стержни 3 Æ 16 (As = 603 мм2) и располагаем их, как показано на черт. 10.
Пример 12. Дано: навесная стеновая панель общественного здания пролетом 5,8 м с поперечным сечением по черт. 11; бетон легкий класса В3,5, марки по средней плотности D1100; арматура класса А-III; нагрузки на панель в стадии эксплуатации: в плоскости панели — собственный вес и вес вышерасположенного остекления (включая простенки) высотой 3м 3,93 кН/м2, из плоскости панели — ветровая нагрузка 0,912 кН/м2,
Требуется проверить прочность панели в стадии эксплуатации.
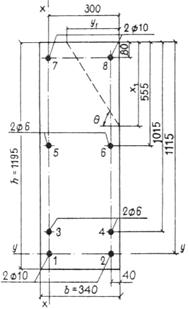
Черт. 11. К примеру расчета 12
1 — 8 — стержни
Расчет. Сначала определим изгибающие моменты, действующие в среднем сечении панели в плоскости и из плоскости панели.
Согласно п. 2.13 определим нагрузку от собственного веса панели. Поскольку класс легкого
бетона ниже В12,5, плотность бетона панели равна g = 1,1D = 1,1·1100 = 1210 кг/м3. Тогда нагрузка от собственного веса панели будет равна:
![]()
а с учетом коэффициента надежности по нагрузке gf = 1,2 (поскольку g < 1800 кг/м3)
![]()
Нагрузка от веса вышерасположенного остекления qg = 3,93 · 3 = 11,8 кН/м.
Итого нагрузка, действующая в плоскости панели, равна:
![]()
а момент в середине панели от этой нагрузки
![]()
Ветровая нагрузка на 1 м длины панели, учитывая передачу нагрузки от выше- и нижерасположенного остекления, равна:
![]()
а момент от этой нагрузки равен:
![]()
Поскольку арматура распределена неравномерно по всему сечению, прочность проверим по формулам общего случая расчета согласно п. 3.76 (с учетом п. 3.13).
Все стержни обозначим номерами, как показано на черт. 11. Через центр наиболее растянутого стержня 1 проводим ось х параллельно размеру h = 1195 мм и ось у — параллельно размеру b = 340 мм.
Угол q между осью у и прямой, ограничивающей сжатую зону, принимаем как при расчете упругого тела на косой изгиб:
![]()
Определим в первом приближении площадь сжатой зоны бетона по формуле (37), т. е. приняв все стержни с полными расчетными сопротивлениями, при этом стержень 8 принимаем сжатым, а остальные стержни — растянутыми.
Для стержней 1, 2, 7, 8 (Æ 10) имеем Rs = Rsc = 365 МПа, а для стержней 3 — 6 (Æ 6) — Rs = 355 МПа, тогда:
![]()
![]()
Поскольку имеет место ветровая нагрузка, значение Rb принимаем с учетом коэффициента gb2 = 1,1, т.е. Rb = 2,3 МПа.
![]()
Площадь сжатой
зоны в предположении треугольной
ее формы определяется по формуле ![]() где
x1 — размер сжатой
зоны по стороне
сечения h, отсюда x1 равен:
где
x1 — размер сжатой
зоны по стороне
сечения h, отсюда x1 равен:
![]()
Размер у1 сжатой зоны по стороне сечения b равен:
![]()
т. е. действительно сжатая зона имеет треугольную форму.
Нанеся эти
размеры на черт. 11, видим, что стержень 8
оказался в сжатой зоне, а все остальные —
в растянутой. Проверим напряжение ssi
в стержнях, ближайших к границе сжатой зоны, т. е. в стержнях 6—8, по формуле
(155), определяя
отношения ![]() по формуле
по формуле ![]() где axi
и ayi —
расстояния от i-го стержня до наиболее сжатой
стороны сечения соответственно в направлении осей х и у.
где axi
и ayi —
расстояния от i-го стержня до наиболее сжатой
стороны сечения соответственно в направлении осей х и у.
Принимая ssc,u = 400 МПа, w = 0,8 – 0,008Rb = 0,8 – 0,008 · 2,3 = 0,782, получим

Вычисления сведем в следующую таблицу:
|
Номер стержня |
Asi, мм2 |
ayi, мм |
axi, мм |
ayi tgq + + axi, мм |
xi |
ssi >< Rs, МПа |
|
6 |
28,3 |
40 |
555 |
662 |
0,719 |
120,9 < 355 |
|
7 |
78,5 |
300 |
80 |
881 |
0,54 |
620 > 365 |
|
8 |
78,5 |
40 |
80 |
187 |
2,545 |
–959 < –365 |
Из таблицы видно, что только для стержня 6 было принято при вычислении Ab неправильное напряжение: 355 МПа вместо 120,9 МПа. Принимаем в этом стержне напряжение несколько большее, чем вычисленное, — ss6 = 160 МПа. Из равенства (154) при N = 0 вычислим значение Ab:

Аналогично
вычислим ![]() мм.
мм.
Отсюда для стержня 6 имеем:
![]()
![]()
т. е. значение ss6 близко к принятому, и, следовательно, Ab и x1 не следует пересчитывать.
Определим моменты внутренних сил относительно осей у и х соответственно Мxu и Мyu.
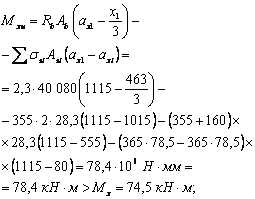
![]()

Поскольку оба внутренних момента превышают обе составляющие внешнего момента, прочность сечения обеспечена.
РАСЧЕТ СЕЧЕНИЙ, НАКЛОННЫХ
К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.28 (3.29). Расчет железобетонных элементов по наклонным сечениям должен производиться для обеспечения прочности:
на действие поперечной силы по наклонной полосе между наклонными трещинами согласно п. 3.30;
на действие поперечной силы по наклонной трещине для элементов с поперечной арматурой согласно пп. 3.31—3.39, для элементов без поперечной арматуры — согласно пп. 3.40 и 3.41;
на действие изгибающего момента по наклонной трещине согласно пп. 3.42—3.47.
Короткие консоли колонн рассчитываются на действие поперечных сил по наклонной сжатой полосе между грузом и опорой согласно п. 3.99.
Балки, нагруженные одной или двумя сосредоточенными силами, располагаемыми не далее h0 от опоры, а также короткие балки пролетом l £ 2h0 рекомендуется рассчитывать на действие поперечной силы, рассматривая прочность наклонной сжатой полосы между грузом и опорой с учетом соответствующих рекомендаций. Допускается производить расчет таких балок как элементов без поперечной арматуры согласно п. 3.40.
Примечание. В настоящем Пособии под поперечной арматурой имеются в виду хомуты и отогнутые стержни (отгибы). Термин „хомуты" включает в себя поперечные стержни сварных каркасов и хомуты вязаных каркасов.
3.29. Расстояния между хомутами s, между опорой и концом отгиба, ближайшего к опоре, s1, а также между концом предыдущего и началом последующего отгибов s2 (черт. 12) должны быть не более величины smax:
![]() (46)
(46)
где jb4 — см. табл. 21.
Кроме того, эти расстояния должны удовлетворять конструктивным требованиям пп. 5.69 и 5.71.
Черт. 12. Расстояния между хомутами, опорой и отгибами
При линейном изменении ширины b по высоте в расчет наклонных сечений [ в формулу (46) и последующие] вводится ширина элемента на уровне середины высоты сечения (без учета полок).
РАСЧЕТ ЭЛЕМЕНТОВ НА ДЕЙСТВИЕ
ПОПЕРЕЧНОЙ СИЛЫ
ПО НАКЛОННОЙ СЖАТОЙ ПОЛОСЕ
3.30 (3.30). Расчет железобетонных элементов на действие поперечной, силы для обеспечения прочности по наклонной полосе между наклонными трещинами должен производиться из условия
![]() (47)
(47)
где Q — поперечная сила в нормальном сечении, принимаемом на расстоянии от опоры не менее h0;
jw1 — коэффициент, учитывающий влияние хомутов, нормальных к оси элемента, и определяемый по формуле
![]() (48)
(48)
но не более 1,3;
здесь ![]()
jb1 — коэффициент, определяемый по формуле
![]() (49)
(49)
здесь b — коэффициент, принимаемый равным для тяжелого и мелкозернистого бетонов — 0,01, для легкого бетона — 0,02;
Rb — в МПа.
РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ
НА ДЕЙСТВИЕ ПОПЕРЕЧНОЙ СИЛЫ
ПО НАКЛОННОЙ ТРЕЩИНЕ
Элементы постоянной высоты,
армированные хомутами без отгибов
3.31. Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине (черт. 13) производится из условия
![]() (50)
(50)
где Q — поперечная сила от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем через наиболее удаленный от опоры конец наклонного сечения; при нагрузке, приложенной к нижней грани элемента или в пределах высоты его сечения, также допускается значение Q принимать в наиболее удаленном от опоры конце наклонного сечения, если хомуты, установленные на действие отрыва согласно п. 3.97, не учитываются в данном расчете, при этом следует учитывать возможность отсутствия временной нагрузки на участке в пределах наклонного сечения;
Qb — поперечное усилие, воспринимаемое бетоном и равное:
![]() (51)
(51)
jb2 — коэффициент, учитывающий вид бетона и определяемый по табл. 21;
jf — коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах и определяемый по формуле
![]() (53)
(53)
но не более 0,5,
при этом
значение ![]() принимается не
более
принимается не
более ![]() ;
;
учет полок производится, если поперечная арматура в ребре заанкерена в полке, где расположена поперечная арматура, соединяющая свесы полки с ребром;
с — длина проекции наклонного сечения на продольную ось элемента, определяемая согласно п. 3.32.
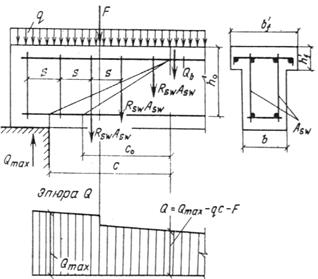
Черт. 13. Схема усилий в наклонном сечении элементов с
хомутами при расчете его на действие поперечной силы
Таблица 21
|
Бетон |
Коэффициенты |
||
|
|
jb2 |
jb3 |
jb4 |
|
Тяжелый |
2,00 |
0,6 |
1,5 |
|
Мелкозернистый |
1,70 |
0,5 |
1,2 |
|
Легкий при марке по средней плотности D: 1900 и выше |
1,90 |
0,5 |
1,2 |
|
1800 и ниже при мелком заполнителе: плотном |
1,75 |
0,4 |
1,0 |
|
пористом |
1,50 |
0,4 |
1,0 |
Значение Qb принимается не менее Qb,min = jb3 (1 + jf) Rbtbh0 (jb3 — см. табл. 21);
Qsw — поперечное усилие, воспринимаемое хомутами и равное:
![]() (54)
(54)
здесь qsw — усилие в хомутах на единицу длины элемента в пределах
наклонного сечения, определяемое по формуле
![]() (55)
(55)
c0 — длина проекции наклонной трещины на продольную ось элемента, принимаемая равной:
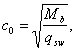 (56)
(56)
но не более с и не более 2h0, а также не менее h0, если c > h0.
При этом для хомутов, устанавливаемых по расчету (т. е. когда не выполняются требования пп. 3.40 и 3.41), должно удовлетворяться условие
![]() (57)
(57)
Разрешается не
выполнять условие (57), если в формуле (52) учитывать такое уменьшенное значение Rbtb, при котором
условие (57) превращается в равенство,
т. е. если принимать ![]() в этом случае всегда принимается
c0 =2h0, но не более
с.
в этом случае всегда принимается
c0 =2h0, но не более
с.
3.32. При проверке условия (50) в общем случае задаются рядом наклонных сечений при различных значениях с, не превышающих расстояния от опоры до сечения с максимальным изгибающим моментом и не более (jb2/jb3)h0.
При действии на элемент сосредоточенных сил значения с принимаются равными расстояниям от опоры до точек приложения этих сил (черт. 14).
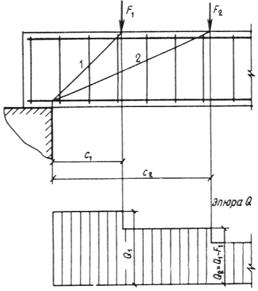
Черт. 14. Расположение расчетных наклонных сечений при
1 — наклонное сечение, проверяемое на действие поперечной
При расчете
элемента на действие равномерно распределенной нагрузки q
значение с принимается равным ![]() а если q1 > 0,56qsw,
следует принимать
а если q1 > 0,56qsw,
следует принимать ![]() где значение q1 определяется следующим образом:
где значение q1 определяется следующим образом:
а) если действует фактическая равномерно распределенная нагрузка, q1 = q;
б) если нагрузка q включает в себя временную нагрузку, которая приводится к эквивалентной равномерно распределенной нагрузке v (когда эпюра моментов М от принятой в расчете нагрузки v всегда огибает эпюру М от любой фактической временной нагрузки), q1 = g + v/2 (где g — постоянная сплошная нагрузка).
При этом значение Q принимается равным Qmax — q1c, где Qmax — поперечная сила в опорном сечении.
3.33. Требуемая интенсивность хомутов, выражаемая через qsw (см. п. 3.31), определяется следующим образом:
а) при
действии на элемент сосредоточенных сил, располагаемых на расстояниях сi от опоры, для
каждого наклонного сечения с длиной проекции сi, не превышающей
расстояния до сечения с максимальным изгибающим моментом, значение qsw определяется в зависимости от
коэффициента ![]() по одной из следующих формул:
по одной из следующих формул:
если
![]()
![]() (58)
(58)
если ![]()
![]() (59)
(59)
если ![]()
![]() (60)
(60)
если ![]()
![]() (61)
(61)
(здесь h0 принимается не более ci).
Окончательно принимается наибольшее значение qsw(i).
В формулах п. 3.33:
Qi — поперечная сила в нормальном сечении, расположенном на расстоянии ci от опоры;
Qbi —определяется по формуле (51) при с = ci;
c0 — принимается равным сi, но не более 2h0;
б) при действии на элемент только равномерно распределенной нагрузки q требуемая интенсивность хомутов определяется по формулам:
при ![]()
![]() (62)
(62)
при ![]()
![]() (63)
(63)
![]() в обоих случаях qsw
принимается не менее
в обоих случаях qsw
принимается не менее ![]() ;
;
при ![]()
![]() (64)
(64)
В случае, если полученное значение qыц не удовлетворяет условию (57), его следует вычислить по формуле
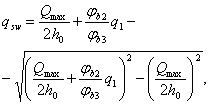
здесь ![]()
Qmax — поперечная сила в опорном сечении;
q1 — см. п. 3.32.
3.34. При уменьшении интенсивности хомутов от опоры к пролету с qsw1 на qsw2 (например, увеличением шага хомутов) следует проверить условие (50) при значениях с, превышающих l1 — длину участка элемента с интенсивностью хомутов qsw1 (черт. 15). При этом значение Qsw принимается равным:
![]()
при ![]()
![]()
при ![]()
![]()
где c01, c02 — определяются по формуле (56) при qsw, соответственно равном qsw1 и qsw2.
Черт. 15. К расчету наклонных сечений при изменении
интенсивности хомутов
При действии на элемент равномерно распределенной нагрузки длина участка с интенсивностью qsw1 принимается не менее значения l1, определяемого следующим образом:
если ![]()
![]()
где  но не
более
но не
более ![]()
при этом, если ![]()
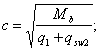
если ![]()
![]()
здесь q1 — см. п. 3.32.
Если для
значения qsw2 не выполняется условие (57),
длина l1
вычисляется при скорректированных согласно п.
3.31 значениях ![]() и
и ![]() при этом
сумма
при этом
сумма ![]() принимается не менее нескорректированного
значения Qb,min.
принимается не менее нескорректированного
значения Qb,min.
Элементы постоянной высоты,
армированные отгибами
3.35. Проверка прочности наклонного сечения на действие поперечной силы для элемента с отгибами производится из условия (50) с добавлением к правой части условия (50) значения
![]() (65)
(65)
где Аs,inc — площадь сечения отгибов, пересекающих опасную наклонную трещину с длиной проекции c0;
q — угол наклона отгибов к продольной оси элемента.
Значение c0
принимается равным длине участка элемента в пределах рассматриваемого
наклонного сечения, для которого выражение
![]() принимает
минимальное значение. Для этого рассматриваются участки от конца наклонного
сечения или от конца отгиба в пределах длины с до начала отгиба, более близкого
к опоре, или до опоры (черт. 16), при
этом длина участка принимается не более значения c0, определяемого по формуле (56), а наклонные трещины, не пересекающие
отгибы, при значениях c0 менее вычисленных по формуле (56) в расчете не рассматриваются.
принимает
минимальное значение. Для этого рассматриваются участки от конца наклонного
сечения или от конца отгиба в пределах длины с до начала отгиба, более близкого
к опоре, или до опоры (черт. 16), при
этом длина участка принимается не более значения c0, определяемого по формуле (56), а наклонные трещины, не пересекающие
отгибы, при значениях c0 менее вычисленных по формуле (56) в расчете не рассматриваются.
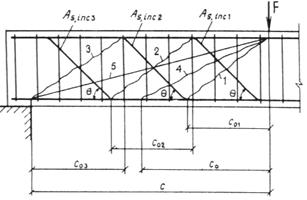
Черт. 16. К определению наиболее опасной наклонной
трещины для элементов с отгибами при расчете на действие
1—4 — возможные наклонные трещины; 5 — рассматриваемое
наклонное сечение
На черт. 16 наиболее опасная наклонная трещина соответствует минимальному значению из следующих выражений:
1 — ![]()
2 — ![]()
3 — ![]()
4 — ![]()
[здесь с0 — см. формулу (56)].
Значения с принимаются равными расстояниям от опоры до концов отгибов, а также до мест приложения сосредоточенных сил; кроме того, следует проверить наклонные сечения, пересекающие последнюю плоскость отгибов и заканчивающиеся на расстоянии c0, определяемом по формуле (56), от начала последней и предпоследней плоскостей отгибов (черт. 17).
Расположение отгибов должно удовлетворять требованиям пп. 3.29, 5.71 и 5.72.
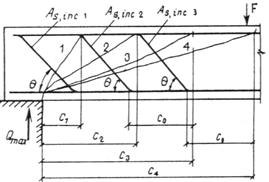
Черт. 17. Расположение расчетных наклонных сечений в
элементе с отгибами
1—4 — расчетные наклонные сечения
Элементы переменной высоты
с поперечным армированием
3.36 (3.33). Расчет элементов с наклонными сжатыми гранями на действие поперечной силы производится согласно пп. 3.31, 3.32, 3.34 и 3.35 с учетом рекомендаций пп. 3.37 и 3.38, принимая в качестве рабочей высоты наибольшее значение h0 в пределах рассматриваемого наклонного сечения (черт. 18, а).
Расчет элементов с наклонными растянутыми гранями на действие поперечной силы также рекомендуется производить согласно пп. 3.31, 3.32, 3.34 и 3.35, принимая в качестве рабочей высоты наибольшее значение h0 в пределах наклонного сечения (черт. 18, б).
а)
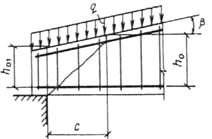
б)
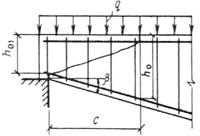
Черт. 18. Балки с переменной высотой сечения
а — сжатой; б — растянутой
Угол b между сжатой и растянутой гранями элемента должен удовлетворять условию tgb < 0,4.
3.37. Для балок без отгибов высотой, равномерно увеличивающейся от опоры к пролету (см. черт. 18), рассчитываемых на действие равномерно распределенной нагрузки q, наклонное сечение проверяется из условия (50) при невыгоднейшем значении с, определяемом следующим образом:
если выполняется условие
![]() (66)
(66)
значение с вычисляется по формуле
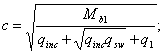 (67)
(67)
если условие (66) не выполняется, значение с вычисляется по формуле
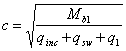 (при этом с0 = с), (68)
(при этом с0 = с), (68)
а также, если ![]()
 (при этом с0 = 2h0), (69)
(при этом с0 = 2h0), (69)
Mb1 — величина Mb, определяемая по формуле (52) как для опорного сечения балки с рабочей высотой h01 без учета приопорного уширения ширины b;
b — угол между сжатой и растянутой гранями балки;
q1 — см. п. 3.32.
Рабочая высота h0 при этом принимаются равной h0 = h01 + ctgb.
При уменьшении интенсивности хомутов от qsw1 у опоры до qsw2 в пролете следует проверить условие (50) при значениях с, превышающих l1 — длину участка элемента с интенсивностью хомутов qsw1, при этом значение Qsw определяется согласно п. 3.34.
Участки балки с постоянным характером увеличения рабочей высоты h0 не должны быть менее принятого значения с.
При действии на балку сосредоточенных сил проверяются наклонные сечения при значениях с, принимаемых согласно п. 3.32, а также, если tgb > 0,1, определяемых по формуле (68) при q1 = 0.
3.38. Для консолей без отгибов высотой, равномерно увеличивающейся от свободного конца к опоре (черт. 19), в общем случае проверяют условие (50), задаваясь наклонными сечениями со значениями с, определяемыми по формуле (68) при q1 = 0 и принимаемыми не более расстояния от начала наклонного сечения в растянутой зоне до опоры. При этом за h01 и Q принимают соответственно рабочую высоту и поперечную силу в начале наклонного сечения в растянутой зоне. Кроме того, проверяют наклонные сечения, проведенные до опоры, если при этом c0 < с.
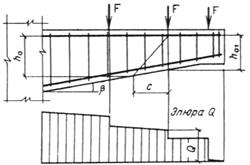
Черт. 19. Консоль высотой, уменьшающейся от опоры
к свободному концу
При действии на консоль сосредоточенных сил начало наклонного сечения располагают в растянутой зоне нормальных сечений, проходящих через точки приложения этих сил (см. черт. 19).
При действии равномерно распределенной нагрузки или нагрузки, линейно увеличивающейся к опоре, консоль рассчитывают так же, как элемент с постоянной высотой сечения согласно пп. 3.31 и 3.32, принимая рабочую высоту h0 в опорном сечении.
Элементы с поперечной арматурой
при косом изгибе
3.39. Расчет на действие поперечной силы элементов прямоугольного сечения, подвергающихся косому изгибу, производится из условия
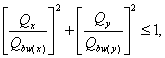 (70)
(70)
где Qx, Qy — составляющие поперечной силы, действующие соответственно в плоскости симметрии х и в нормальной к ней плоскости у в наиболее удаленном от опоры конце наклонного сечения;
Qbw(x), Qbw(y) — предельные поперечные силы, воспринимаемые наклонным сечением при действии их соответственно в плоскостях х и у и принимаемые равными правой части условия (50).
При действии на элемент равномерно распределенной нагрузки допускается определять значения с согласно п. 332 для каждой плоскости х и у.
Примечание. Отгибы при расчете на поперечную силу при косом изгибе не учитываются.
Элементы без поперечной арматуры
3.40 (3.32). Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий:
a) ![]() (71)
(71)
где Qmax — максимальная поперечная сила у грани опоры;
б) ![]() (72)
(72)
где Q — поперечная сила в конце наклонного сечения;
jb4 — коэффициент, определяемый по табл. 21;
с — длина проекции наклонного сечения, начинающегося от опоры; значение с принимается не более сmax = 2,5h0.
В сплошных плоских плитах с несвободными боковыми краями (соединенными с другими элементами или имеющими опоры) допускается указанное значение сmax делить на коэффициент a:
![]() (73)
(73)
но не более 1,25.
При проверке условия (72) в общем случае задаются рядом значений с, не превышающих сmax.
При действии на элемент сосредоточенных сил значения с принимаются равными расстояниям от опоры до точек приложения этих сил (черт. 20).
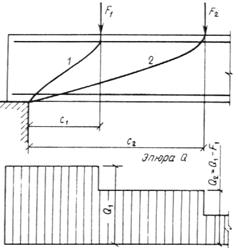
Черт. 20. Расположение невыгоднейших наклонных сечений
в элементах без поперечной арматуры
1 — наклонное сечение, проверяемое на действие поперечной
При расчете элемента на действие распределенных нагрузок, если выполняется условие
![]() (74)
(74)
значение с в условии (72) принимается равным cmax, а при невыполнении условия (74) —
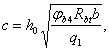 (75)
(75)
здесь q1 принимается при действии равномерно распределенной нагрузки в соответствии с п. 3.32, а при действии сплошной нагрузки с линейно изменяющейся интенсивностью — равной средней интенсивности на приопорном участке длиной, равной четверти пролета балки (плиты) или половине вылета консоли, но не более сmax.
3.41. Для элементов с переменной высотой сечения при проверке условия (71) значение h0 принимается в опорном сечении, а при проверке условия (72) — как среднее значение h0 в пределах наклонного сечения.
Для элементов
с высотой сечения, увеличивающейся с увеличением
поперечной силы, значение
cmax принимается
равным ![]() при этом для сплошных плоских плит,
указанных в п. 3.40,
при этом для сплошных плоских плит,
указанных в п. 3.40, ![]()
где h01 — рабочая высота в опорном сечении;
b — угол между растянутой и сжатой гранями элемента;
a — см. формулу (73), где h допускается принимать по опорному сечению.
При действии на такой элемент распределенной нагрузки значение с в условии (72) принимается равным:
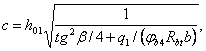 (76)
(76)
но не более сmax, где q1 — см. п. 3.40.
РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ
НА ДЕЙСТВИЕ ИЗГИБАЮЩЕГО МОМЕНТА
3.42 (3.35). Расчет элементов на действие изгибающего момента для обеспечения прочности по наклонной трещине (черт. 21) должен производиться из условия
![]() (77)
(77)
где М — момент от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения, относительно оси, перпендикулярной плоскости действия момента и проходящей через точку приложения равнодействующей усилий Nb в сжатой зоне (черт. 22);
RsAszs, — сумма моментов относительно той же оси от усилий
SRswAswzsw, соответственно в продольной арматуре, хомутах и
SRswAs,inczs,inc отгибах, пересекающих растянутую зону наклонного сечения;
zs, zsw, zs,inc — расстояния от плоскостей расположения соответственно продольной арматуры, хомутов и отгибов до указанной оси.
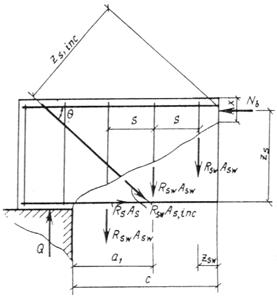
Черт. 21. Схема усилий в наклонном сечении при расчете
его по изгибающему моменту
Высота сжатой зоны наклонного сечения, измеренная по нормали к продольной оси элемента, определяется из условия равновесия проекций усилий в бетоне сжатой зоны и в арматуре, пересекающей наклонное сечение, на продольную ось элемента согласно пп. 3.15 и 3.20. При наличии в элементе отгибов в числитель выражения для х добавляется величина SRswAs,inccosq (где q — угол наклона отгибов к продольной оси элемента).
Величину zs допускается принимать равной h0 — 0,5х, но при учете сжатой арматуры не более h0 – а’.
Величина SRswAswzsw при хомутах постоянной интенсивности определяется по формуле
![]() (78)
(78)
где qsw — усилие в хомутах на единицу длины (см. п. 3.31);
с — длина проекции наклонного сечения на продольную ось элемента, измеренная между точками приложения равнодействующих усилий в растянутой арматуре и сжатой зоне (см. п. 3.45).
Величины zs,inc для каждой плоскости отгибов определяются по формуле
![]() (79)
(79)
где а1 — расстояние от начала наклонного сечения до начала отгиба в растянутой зоне (см. черт. 21).
а)
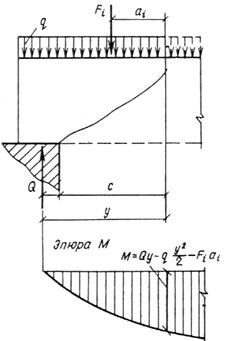
б)
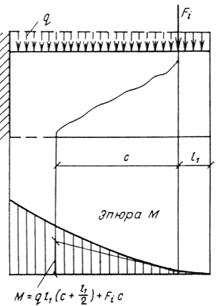
Черт. 22. Определение расчетного значения момента
при расчете наклонного сечения
а — для свободно опертой балки; б — для консоли
3.43 (3.35). Расчет наклонных сечений на действие момента производится в местах обрыва или отгиба продольной арматуры, а также у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров.
Кроме того, расчет наклонных сечений на действие момента производится в местах резкого изменения конфигурации элементов (подрезок, узлов и т. п.).
Расчет наклонных сечений на действие момента допускается не производить при выполнении условий (71) и (72) с умножением их правых частей на 0,8 и при значении с не более 0,8cmax.
3.44. При пересечении наклонного сечения с продольной растянутой арматурой, не имеющей анкеров, в пределах зоны анкеровки расчетное сопротивление этой арматуры Rs снижается путем умножения на коэффициент условий работы gs5, равный:
![]() (80)
(80)
где lx — расстояние от конца арматуры до точки пересечения наклонного сечения с продольной арматурой;
lan — длина зоны анкеровки, определяемая по формуле
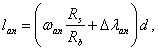 (81)
(81)
здесь wan, Dlan — коэффициенты, принимаемые равными:
для крайних свободных опор балок wan = 0,5, Dlan = 8;
для свободных концов консолей wan = 0,7; Dlan = 11.
В случае применения гладких стержней коэффициент wan принимается равным для опор балок и концов консолей соответственно 0,8 и 1,2.
При наличии на
крайних свободных опорах косвенной или поперечной арматуры, охватывающей без приваривания продольную арматуру, коэффициент wan
делится на величину 1 +12mv, а коэффициент Dlan
уменьшается на величину 10sb/Rb, здесь mv — объемный коэффициент армирования, определяемый для
сварных сеток по формуле (99),
для хомутов — по формуле ![]() (где Asw и s — соответственно площадь сечения огибающего хомута и его шаг), в любом случае значение mv принимается не
более 0,06.
(где Asw и s — соответственно площадь сечения огибающего хомута и его шаг), в любом случае значение mv принимается не
более 0,06.
Напряжение сжатия бетона на опоре sb определяется делением опорной реакции на площадь опирания элемента и принимается не более 0,5Rb.
Длина lan принимается для свободных концов консолей не менее 20d или 250 мм, при этом длину анкеровки lan можно определить с учетом данных табл. 45 (поз. 1).
В случае приваривания к продольным растянутым стержням поперечной или распределительной арматуры учитываемое в расчете усилие в продольной арматуре RsАs увеличивается на величину
![]() (82)
(82)
В формуле (82):
пw - число приваренных стержней по длине lx;
jw — коэффициент, принимаемый по табл. 22;
dw — диаметр приваренных стержней.
Таблица 22
|
dw |
6 |
8 |
10 |
12 |
14 |
|
jw |
200 |
150 |
120 |
100 |
80 |
Окончательно значение RsАs принимается не более значения RsАs, определенного без учета gs5 и Nw.
3.45. Для свободно опертых балок невыгоднейшее наклонное сечение начинается от грани опоры и имеет длину проекции с для балок с постоянной высотой сечения, равную:
![]() (83)
(83)
но не более максимальной длины приопорного участка, за пределами которого выполняется условие (72) с умножением правой части на 0,8 и при значении с не более 0,8cmax.
В формуле (83):
Q — поперечная сила в опорном сечении;
Fi, q — нагрузки соответственно сосредоточенная и равномерно распределенная в пределах наклонного сечения;
As,inc — площадь сечения отгибов, пересекающих наклонное сечение;
q — угол наклона отгибов к продольной оси элемента;
qsw — то же, что в формуле (55).
Если значение с, определенное с учетом сосредоточенной силы Fi, будет меньше расстояния от грани опоры до силы Fi, а определенное без учета силы Fi — больше этого расстояния, за значение с следует принимать расстояние до силы Fi.
Если в пределах длины с хомуты изменяют свою интенсивность с qsw1 у начала наклонного сечения на qsw2, значение с определяется по формуле (83) при qsw = qsw2 и при уменьшении числителя на величину (qsw1 – qsw2)l1 (где l1 — длина участка с интенсивностью хомутов qsw1).
Для балок, нагруженных равномерно распределенной нагрузкой q, с постоянной интенсивностью хомутов без отгибов условие (77) можно заменить условием
![]() (84)
(84)
где Q — поперечная сила в опорном сечении;
М0 — момент в сечении по грани опоры.
Для консолей, нагруженных сосредоточенными силами (черт. 22, б), невыгоднейшее наклонное сечение начинается от мест приложения сосредоточенных сил вблизи свободного конца и имеет длину проекции с для консолей с постоянной высотой, равную:
![]() (85)
(85)
но не более расстояния от начала наклонного сечения до опоры (здесь Q1 — поперечная сила в начале наклонного сечения).
Для консолей, нагруженных только равномерно распределенной нагрузкой q, невыгоднейшее наклонное сечение заканчивается в опорном сечении и имеет длину проекции с, равную:
![]() (86)
(86)
при этом, если с < l – lan, расчет наклонного сечения можно не производить.
В формуле (86):
Аs — площадь сечения арматуры, доводимой до свободного конца;
zs — см. п. 3.42; значение zs определяется для опорного сечения;
lan — длина зоны анкеровки (см. п. 3.44).
Для элементов с высотой сечения, увеличивающейся с увеличением изгибающего момента, при определении длины проекции невыгоднейшего сечения по формулам (83) или (85) числители этих формул уменьшаются на величину RsAstgb — при наклонной сжатой грани и на величину RsAssinb — при наклонной растянутой грани (где b) — угол наклона грани к горизонтали) .
3.46. Для обеспечения прочности наклонных сечений на действие изгибающего момента в элементах постоянной высоты с хомутами продольные растянутые стержни, обрываемые в пролете, должны заводиться за точку теоретического обрыва (т. е. за нормальное сечение, в котором внешний момент становится равным несущей способности сечения без учета обрываемых стержней; черт. 23) на длину не менее величины w, определяемой по формуле
![]() (87)
(87)
где Q — поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва;
As,inc, q — обозначения те же, что в формуле (83);
d — диаметр обрываемого стержня;
qsw — см. п. 3.31.
Для балок с наклонной сжатой гранью числитель формулы (87) уменьшается на RsAstgb, а для балок с наклонной растянутой гранью — на RsAssinb (где b — угол наклона грани к горизонтали). Кроме того, должны быть учтены требования п. 5.44.
Для элементов без поперечной арматуры значение w принимается равным 10d, при этом место теоретического обрыва должно находиться на участке элемента, на котором выполняется условие (72), с умножением правой части на 0,8 и при значении с не более 0,8сmax.
Черт. 23. Обрыв растянутых стержней в пролете
1 — точка теоретического обрыва; 2 — эпюра М
3.47. Для обеспечения прочности наклонных сечений на действие изгибающего момента начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень полностью используется по моменту, не менее чем на h0/2, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету.
РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ В ПОДРЕЗКАХ
3.48. Для элементов с резко меняющейся высотой сечения (например, для балок и консолей, имеющих подрезки), производится расчет по поперечной силе для наклонных сечений, проходящих у опоры консоли, образованной подрезкой (черт. 24), согласно пп. 3.31—3.39, при этом в расчетные формулы вводится рабочая высота h01 короткой консоли, образованной подрезкой.
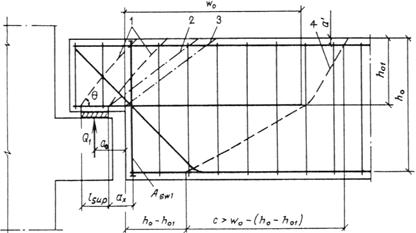
Черт. 24. Невыгодиейшие наклонные сечения
в элементе с подрезкой
1 — наклонная сжатая полоса; 2 — при расчете по поперечной силе;
3 — то же, по изгибающему моменту; 4 — то же, по изгибающему
моменту вне подрезки
Хомуты, необходимые для обеспечения прочности наклонного сечения, следует устанавливать за конец подрезки на участке длиной не менее w0, определяемой по формуле (88).
3.49. Для свободно опертых балок с подрезками должен производиться расчет на действие изгибающего момента в наклонном сечении, проходящем через входящий угол подрезки (см. черт. 24), согласно пп. 3.42—3.45. При этом продольная растянутая арматура в короткой консоли, образованной подрезкой, должна быть заведена за конец подрезки на длину не менее lan (см. п. 5.44) и не менее величины w0, равной:
![]() (88)
(88)
где Q1 — поперечная сила в нормальном сечении у конца подрезки;
Asw1 —площадь сечения дополнительных хомутов, расположенных у конца подрезки на участке длиной не более h01/4 и не учитываемых при определении интенсивности хомутов qsw у подрезки;
As,inc — площадь сечения отгибов, проходящих через входящий угол подрезки;
a0 — расстояние от опоры консоли до конца подрезки;
d — диаметр обрываемого стержня.
Хомуты и отгибы, установленные у конца подрезки, должны удовлетворять условию
![]() (89)
(89)
где h01, h0 — рабочая высота соответственно в короткой консоли подрезки и в балке вне подрезки.
Если нижняя арматура элемента не имеет анкеров, должна быть также проверена, согласно пп. 3.42—3.45, прочность наклонного сечения, расположенного вне подрезки и начинающегося за указанными хомутами на расстоянии не менее h0—h01 от торца (см. черт. 24). При этом в расчете не учитывается продольная арматура короткой консоли, а длина проекции с принимается не менее расстояния от начала наклонного сечения до конца указанной арматуры. Кроме того, длина анкеровки lan для нижней арматуры элемента принимается как для свободных концов консолей.
Расчет
короткой консоли подрезки производится согласно пп. 3.99 и 3.100, принимая
направление наклонной сжатой полосы от наружного края площадки опирания до
равнодействующей усилий в дополнительных хомутах площадью сечения Asw1 на уровне сжатой арматуры балок, т. е. при ![]() (где lsup — см. п.
3.99, ax — см.
черт. 24), при этом в формуле (207) коэффициент 0,8 заменяется на 1,0.
(где lsup — см. п.
3.99, ax — см.
черт. 24), при этом в формуле (207) коэффициент 0,8 заменяется на 1,0.
ПРИМЕРЫ РАСЧЕТА
Расчет наклонных сечений
на действие поперечной силы
Пример 13. Дано: железобетонная плита перекрытия с размерами поперечного сечения по черт. 25; бетон тяжелый класса В15 (Rb = 7,7 МПа и Rbt = 0,67 МПа при gb2 = 0,9; Eb = 20,5 · 103 МПа); ребро плиты армировано плоским сварным каркасом с поперечными стержнями из арматуры класса А-III, диаметром 8 мм (Asw = 50,3 мм2; Rsw = 285 МПа; Es = 2 · 105 МПа), шагом s = 100 мм; временная эквивалентная нагрузка v = 18 кН/м; нагрузка от собственного веса плиты и пола g = 3,9 кН/м; поперечная сила на опоре Qmax = 62 кН.
Требуется проверить прочность наклонной полосы ребра между наклонными трещинами, а также прочность наклонных сечений по поперечной силе.
Черт. 25. К примеру расчета 13
Расчет. h0 = 350 – 58 = 292 мм. Прочность наклонной полосы проверим из условия (47).
Определим коэффициенты jw1 и jb1:
![]()
![]()
отсюда jw1 = 1 + 5amw = 1 + 5 · 9,76 · 0,0059 = 1,29 < 1,3;
для тяжелого бетона b = 0,01;
![]()
тогда ![]()
т. е. прочность наклонной полосы обеспечена.
Прочность наклонного сечения по поперечной силе проверим из условия (50).
Определим величины Mb и qsw:
![]() (см. табл. 21);
(см. табл. 21);
так как ![]() , принимаем
, принимаем
![]() – b = 150 мм, тогда:
– b = 150 мм, тогда:
![]()
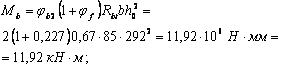
![]() Н/мм (кН/м).
Н/мм (кН/м).
Определим значение Qb,min, принимая jb3 = 0,6:
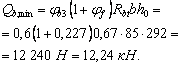
Поскольку ![]()
условие (57) выполняется, и, следовательно, значение Мb не корректируем.
Согласно п. 3.32 определим длину проекции невыгоднейшего наклонного сечения с:
![]() кН/м (Н/мм),
кН/м (Н/мм),
поскольку 0,56qsw = 0,56 · 143 == 80 кН/м > q1 = 12,9 кН/м, значение с определим только по формуле
![]() м.
м.
Тогда ![]()
![]() кН.
кН.
Длина проекции наклонной трещины равна:
![]()
Поскольку c0 = 0,288 < h0 = 0,292 м, принимаем c0 = h0 = 0,292 м, тогда Qsw = qswc0 = 143 · 0,292 = 41,8 кН.
Проверим условие (50):
![]()
т. е. прочность наклонного сечения по поперечной силе обеспечена. Кроме того, должно выполняться требование п. 3.29:
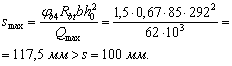
Условия п. 5.69 s < h/2 = 350/2 = 175 мм и s < 150 мм также выполняются.
Пример 14. Дано: свободно опертая железобетонная балка перекрытия пролетом l = 5,5 м; временная равномерно распределенная эквивалентная нагрузка на балку v = 36 кН/м; постоянная нагрузка g = 14 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, h0 = 370 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа; Rbt = 0,67 МПа при gb2 = 0,9); хомуты из арматуры класса А-I (Rsw = 175 МПа).
Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как может быть увеличен шаг хомутов.
Расчет. Наибольшая поперечная сила в опорном сечении равна:
![]() кН,
кН,
где q = v + g = 36 +14 = 50 кН/м.
Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.33б.
Из формулы (52) при jf = 0 и jb2 = 2,0 (см. табл. 21) получим
![]()
Согласно п. 3.32,
![]() кН/м (Н/мм);
кН/м (Н/мм);
![]() кН.
кН.
Так как
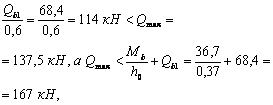
интенсивность хомутов определим по формуле (63) :
![]() кН/м (Н/мм).
кН/м (Н/мм).
При этом, поскольку
![]() Н/мм < 130 Н/мм,
Н/мм < 130 Н/мм,
оставляем qsw = 130 Н/мм.
Согласно п. 5.69, шаг s1 у опоры
должен быть не более h/2 = 200
и 150 мм, а в пролете ![]() = 300 и 500 мм. Максимально допустимый шаг у опоры,
согласно п. 3.29, равен:
= 300 и 500 мм. Максимально допустимый шаг у опоры,
согласно п. 3.29, равен:
![]() мм.
мм.
Принимаем шаг хомутов у опоры s1 = 150 мм, а в пролете — 2s1 = 300 мм, отсюда
![]() мм2.
мм2.
Принимаем в поперечном сечении два хомута диаметром по 10 мм (Аsw= 157 мм2).
Таким образом, принятая интенсивность хомутов у опоры и в пролете балки будет соответственно равна:
![]() Н/мм;
Н/мм;
![]() Н/мм.
Н/мм.
Проверим условие (57), вычислив Qb,min:
![]() H.
H.
Тогда
![]()
![]()
Следовательно, значения qsw1 и qsw2 не корректируем.
Определим, согласно п. 3.34, длину участка l1 с интенсивностью хомутов qsw1. Так как qsw1 — qsw2 = qsw2 = 91,6 H/мм > q1 = 32 Н/мм, значение l1 вычислим по формуле
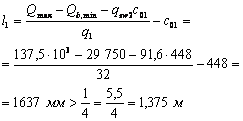
(здесь ![]() мм).
мм).
Принимаем длину участка с шагом хомутов s1 = 150 мм равной 1,64 м.
Пример 15. Дано: железобетонная балка покрытия, нагруженная сосредоточенными силами, как показано на черт. 26, а; размеры поперечного сечения — по черт. 26, б, бетон тяжелый класса В15 (Rbt = 0,67 МПа при gb2 = 0,9); хомуты из арматуры класса А-I (Rsw = 175 МПа).
Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии и как может быть увеличен шаг хомутов.
Расчет. Сначала определим, согласно п. 3.31, величину Mb:
![]() (см. табл. 21);
(см. табл. 21);
![]() мм (см. черт. 26, б);
мм (см. черт. 26, б);
![]()
![]() мм;
мм;
![]()
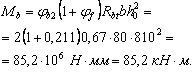
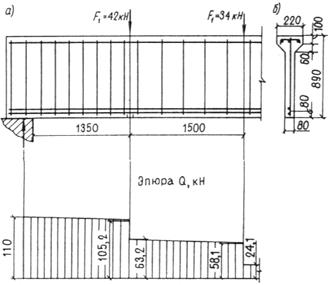
Черт. 26. К примеру расчета 15
Определим требуемую интенсивность хомутов согласно п. 3.33а, принимая длину проекции наклонного сечения с равной расстоянию от опоры до первого груза — с1 = 1,35 м.
Поперечная сила на расстоянии с1 от опоры равна Q1 = 105,2 кН (см. черт. 26).
Из формулы (51) имеем
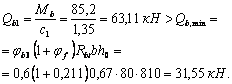
Тогда ![]()
Поскольку с1 = 1,35 м < 2р0 = 2 · 0,81 = 1,62 м,
принимаем с0 = с1 = 1,35 м;
![]()
Так как c01 = 0,417 < c1 = 0,667 < с1/с0 = 1, значение qsw(1) определим по формуле (59):
![]() кН/м.
кН/м.
Определим qsw при значении с, равном расстоянию от опоры до второго груза — c2 = 2,85 м.
![]()
Принимаем Qb2 = Qb,min = 31,55 кН.
Соответствующая поперечная сила равна Q2 = 58,1 кН. Поскольку c2 = 2,85 м > 2h0 = 1,62 м, принимаем c0 = 2h0 = 1,62 м.
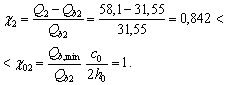
Следовательно, значение qsw(2) определим по формуле (58):
![]() кН/м.
кН/м.
Принимаем максимальное значение qsw = qsw(1) = 31,18 кН/м.
Из условия сварки (см. п. 5.13) принимаем диаметр хомутов 6 мм (Asw = 28,3 мм2), тогда шаг хомутов в приопорном участке равен:
![]() мм.
мм.
Принимаем s1 = 150 мм. Назначаем шаг хомутов в пролете равным s2 = 2s1 = 2 · 150 = 300 мм. Длину участка с шагом s1 определим из условия обеспечения прочности согласно п. 3.34, при этом
![]() Н/мм;
Н/мм;
![]() Н/мм;
Н/мм;
![]() Н/мм.
Н/мм.
Зададим длину участка с шагом хомутов s1 равной расстоянию от опоры до первого груза — l1 = 1,35 м; проверим условие (50) при значении с, равном расстоянию от опоры до второго груза — с = 2,85 м > l1. Значение c01 определим по формуле (56) при qsw1 = 33 кН/м:
![]()
Поскольку с – l1 = 2,85 —1,35 = 1,5 м < c01 = 1,6м, значение Qsw в условии (50) принимаем равным:
![]()
![]() кН;
кН;
![]()
т. е. прочность этого наклонного сечения обеспечена.
Большее значение с не рассматриваем, поскольку при этом поперечная сила резко уменьшается.
Таким образом, длину участка с шагом хомутов s1 = 150 мм принимаем равной l1 = 1,35м.
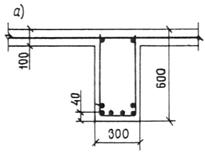
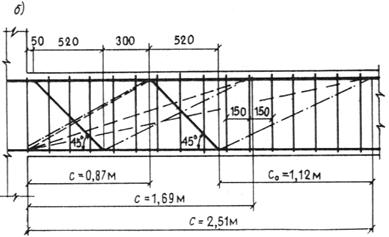
Условные обозначения:
- - - - расчетные наклонные сечения;
-·-·-·- рассматриваемые наклонные трещины
Черт. 27. К примеру расчета 16
Пример 16. Дано: железобетонная балка монолитного перекрытия с размерами поперечного сечения по черт. 27, а; расположение отогнутых стержней — по черт. 27, б; временная эквивалентная нагрузка на балку v = 96 кН/м, постоянная — g = 45 кН/м; поперечная сила на опоре Qmax = 380 кН; бетон тяжелый класса В15 (Rbt = 0,67 МПа при gb2 = 0,9); хомуты двухветвевые диаметром 6 мм (Asw = 57 мм2) из арматуры класса А-I (Rsw = 175 МПа), шагом s = 150 мм; отогнутые стержни класса А-II (Rsw = 225 МПа), площадью сечения: первой плоскости Аs,inc1 = 628 мм2 (2 Æ 20), второй — Аs,inc2 = 402 мм2 (2 Æ 16).
Требуется проверить прочность наклонных сечений по поперечной силе.
Расчет. h0 = 600 – 40 = 560 мм. Согласно п. 3.31 находим значения Mb и qsw:
![]() (см. табл. 21);
(см. табл. 21);
![]() мм;
мм;
![]()
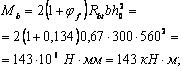
![]() Н/мм.
Н/мм.
Согласно п. 3.32 находим q1 = g + v/2 = 45 + 96/2 = 93 кН/м.
Проверим из условия (50) с учетом формулы (65) наклонное сечение с длиной проекции, равной расстоянию от опоры до конца второй плоскости отгибов, т. е. при с = 50 + 520 + 300 = 870 мм = 0,87 м.
Поперечная сила на расстоянии с = 0,87 м от опоры равна:
![]() кН.
кН.
Определим проекцию опасной наклонной трещины c0 согласно п. 3.35.
Сначала определим максимальное значение c0 по формуле (56):
![]()
принимаем c0,max = 1,12 м. Поскольку с = 0,87 м < c0,max = 1,12 м, принимаем для этого наклонного сечения c0 = с = 0,87 м. Наклонную трещину, расположенную между концом второй и началом первой плоскостей отгибов, т. е. не пересекающую отгибы, в расчете не рассматриваем, так как для нее c0 = 0,30 м < c0,max.
Для первой плоскости отгибов
![]()
Тогда
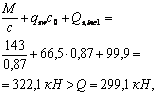
т. е. прочность данного наклонного сечения обеспечена.
Проверим наклонное сечение, оканчивающееся на расстоянии c0 = 1,12 м от начала первой плоскости отгибов, т.е. при с = 0,05 + 0,52 + 1,12 = 1,69 м.
Поперечная сила на расстоянии с = 1,69 м от опоры равна Q = 380 –93 · 1,69 = 222,8 кН.
Для второй плоскости отгиба
![]()
Для этого сечения принимаем наклонную трещину, проведенную от конца наклонного сечения до начала первой плоскости отгибов, т.е. c0 = c0,max = 1,12 м. Наклонные трещины, проведенные от конца наклонного сечения до опоры и до начала второй плоскости отгибов, не рассматриваем, так как в первом случае c0 = с = 1,69 м > c0,max = 1,12 м, а во втором — трещина не пересекает отгибы при c0 < c0,max.
Тогда
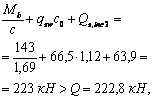
т. е. прочность данного наклонного сечения обеспечена.
Проверим наклонное сечение, оканчивающееся на расстоянии c0,max = 1,12 м от начала второй плоскости отгибов, т. е. при с = 0,05 + 0,52 + 0,30 + 0,52 + 1,12 = 2,51 м.
Поперечная сила на расстоянии с = 2,51 м от опоры равна Q = 380 –93 · 2,51 = 146,6 кН.
Для этого
сечения, очевидно, c0 = c0,max = 1,12 м
и наклонная трещина отгибы не пересекает,
т. е. Qs,inc = 0. Поскольку c = 2,51 м ![]() 1,87 м, принимаем
Qb = Qb,min
1,87 м, принимаем
Qb = Qb,min 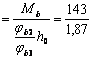 = 76,5 кН
= 76,5 кН
Тогда Qb + qswc0 + Qs,inc = 76,5 + 66,5 · 1,12 + 0 = 151 кН > Q = 146,6 кН, т. е. прочность любых наклонных сечений обеспечена.
Согласно п. 3.29 проверим расстояние между началом первой плоскости отгибов и концом второй плоскости, принимая поперечную силу у конца второй плоскости отгибов Q = 299,1 кН и jb4 = 1,5:
![]()
т. е. требование п. 3.29 выполнено.
Пример 17. Дано: железобетонная двускатная балка покрытия пролетом 8,8 м; сплошная равномерно распределенная нагрузка на балку q = 46 кН/м (черт. 28, a); размеры поперечного сечения — по черт. 28, б; бетон тяжелый класса В25 (Rbt = 0,95 МПа при gb2 = 0,9); хомуты из арматуры класса А-I (Rsw = 175 МПа), диаметром 8 мм (Asw = 50,3 мм2), шагом s = 150 мм.
Требуется проверить прочность наклонных сечений по поперечной силе.
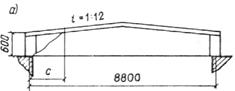
Черт. 28. К примеру расчета 17
Расчет производим согласно п. 3.37.
Рабочая высота опорного сечения равна h01 = 600 – 80 = 520 мм (черт. 28, б).
Определим величины jf1 и Мb1 по формулам (53) и (52) как для опорного сечения:
![]() мм;
мм;
![]()
![]()
принимаем jf1 = 0,5; jb2 = 2 (см. табл. 21);
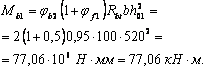
По формуле (55) определим величину qsw:
![]() Н/мм (кН/м).
Н/мм (кН/м).
Определим значение qinc, принимая tgb = 1/12:
![]() Н/мм (кН/м).
Н/мм (кН/м).
Поскольку нагрузка сплошная, принимаем q1 = q = 46 кН/м.
Проверим условие (66):
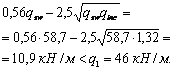
Условие (66) не выполняется, и, следовательно, значение с вычислим по формуле (68):

при этом c0 = с = 0,853 м.
Рабочая высота поперечного сечения h0 на расстоянии с = 0,853 м от опоры равна:
![]() м.
м.
Определим величину Mb при h0 = 591 мм:
![]()
принимаем jf = 0,5;
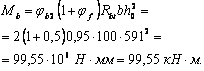
Проверим условие (50), принимая поперечную силу в конце наклонного сечения равной:
![]() кН;
кН;
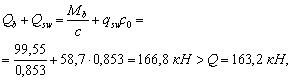
т. е. прочность наклонных сечений по поперечной силе обеспечена.
Пример 18. Дано: консоль размерами по черт. 29; сосредоточенная сила на консоли F = 300 кН, расположенная на расстоянии 0,8 м от опоры; бетон тяжелый класса В15 (Rbt = 0,67 МПа при gb2 = 0,9); хомуты двухветвевые диаметром 8 мм (Asw = 101 мм2) из арматуры класса А-I (Rsw = 175 МПа), шагом s = 200 мм.
Требуется проверить прочность наклонных сечений по поперечной силе.
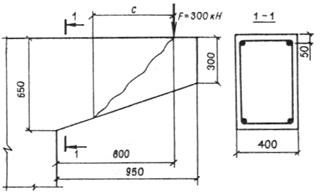
Черт. 29. К примеру расчета 18
Расчет. Согласно п. 3.38 проверим из условия (50) наклонное сечение, начинающееся от места приложения сосредоточенной силы, при значении с, определяемом по формуле (68).
Рабочая высота
в месте приложения сосредоточенной силы равна ![]() мм (см.
черт. 29).
мм (см.
черт. 29).
По формуле (52) определим величину Mb1, принимая jb2 = 2 (см. табл. 21) и jf = 0:
![]() Н · мм.
Н · мм.
Значение qsw равно:
![]() Н/мм (кН/м).
Н/мм (кН/м).
Принимая ![]() (см.
черт. 29), определим qinc:
(см.
черт. 29), определим qinc:
![]() Н/мм,
Н/мм,
отсюда, принимая q1 = 0, имеем
![]() мм,
мм,
при этом c0 = c = 556 мм.
Поскольку значение с не превышает значения расстояния от груза до опоры, оставим с = 556 мм и определим рабочую высоту h0 в конце наклонного сечения:
![]() мм.
мм.
Поскольку 2h0 = 2 · 510 мм > c0 = 558 мм, оставим c0 = 556 мм.
Значение Mb равно:
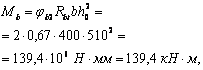
отсюда

т. е. прочность этого наклонного сечения обеспечена.
Для наклонного сечения, располагаемого от груза до опоры, по формуле (56) определим значение c0, принимая h0 = 650 – 50 = 600 мм:
![]() Н · мм;
Н · мм;
![]()
принимаем c0 = 2h0 = 1200 мм.
Поскольку c0 = 1200 мм > с = 800 мм, указанное наклонное сечение можно не проверять. Следовательно, прочность любого наклонного сечения обеспечена.
Пример 19. Дано: сплошная плита перекрытия без поперечной арматуры размером 3х6 м, толщиной h = 160 мм, монолитно связанная по периметру с балками; эквивалентная временная равномерно распределенная нагрузка на плиту v = 50 кН/м2; нагрузка от собственного веса и пола g = 9 кН/м2; a = 20 мм; бетон тяжелый класса В25 (Rbt = 0,95 МПа при gb2 = 0,9).
Требуется проверить прочность плиты на действие поперечной силы.
Расчет. h0 = h – а = 160 – 20 = 140 мм. Расчет производим для полосы шириной b = 1 м = 1000 мм, пролетом l = 3 м; полная нагрузка на плиту равна q = v + g = 50 + 9 = 59 кН/м.
Поперечная сила на опоре равна:
![]() кН.
кН.
Проверим условие (71):
![]()
Проверим условие (72). Поскольку боковые края плиты связаны с балками, значение cmax определим с учетом коэффициента a = 1 + 0,05b/h = 1 + 0,05 · 6/0,16 > 1,25 (здесь b = 6 м — расстояние между боковыми краями плиты), т. е. a = 1,25:
![]() мм.
мм.
Согласно п. 3.32 имеем:
![]()
![]() (см. табл. 21).
(см. табл. 21).
Поскольку ![]() 356 Н/мм > q1 = 34 Н/мм, принимаем с = cmax = 280 мм = 0,28 м.
356 Н/мм > q1 = 34 Н/мм, принимаем с = cmax = 280 мм = 0,28 м.
Поперечная сила в конце наклонного сечения равна Q = Qmax – q1c = 88,5 – 34 · 0,28 = 79 кН.
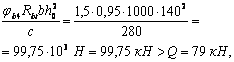
т. е. прочность плиты по поперечной силе обеспечена.
Пример 20. Дано: панель резервуара консольного типа с переменной толщиной от 262 (в заделке) до 120 мм (на свободном конце), вылетом 4,25 м; боковое давление грунта, учитывающее нагрузки от транспортных средств на поверхности грунта, линейно убывает от q0 = 69 кН/м2 в заделке до q = 7 кН/м2 на свободном конце; а = 22 мм; бетон тяжелый класса В15 (Rbt = 0,82 МПа при gb2 = 1,1).
Требуется проверить прочность панели по поперечной силе.
Расчет. Рабочая высота сечения панели в заделке равна h01 = 262 – 22 = 240 мм.
Определим tgb (b — угол между растянутой и сжатой гранями):
![]()
Расчет производим для полосы панели шириной b = 1 м = 1000 мм.
Проверим условия п. 3.40. Поперечная сила в заделке равна:
![]() кН.
кН.
Проверим условие (71), принимая h0 = h01 = 240 мм:
![]()
т. е. условие выполняется.
Поскольку панели связаны одна с другой, а ширина стенки резервуара заведомо более 5h, значение cmax определим с учетом коэффициента a = 1,25:
![]() мм.
мм.
Средняя
интенсивность нагрузки на приопорном участке длиной cmax = 464
мм равна q1 = 69 – (69 – 7) ![]() = 65,6 Н/мм.
= 65,6 Н/мм.
Из табл. 21 jb4 =1,5.
Поскольку
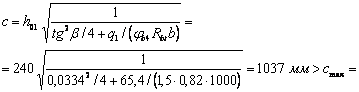
= 464 мм, принимаем с = сmax = 464 мм.
Определим
рабочую высоту сечения на расстоянии ![]() от опоры (т. е.
среднее значение h0
в пределах длины с):
от опоры (т. е.
среднее значение h0
в пределах длины с):
![]() мм.
мм.
Поперечная сила на расстоянии с == 464 мм от опоры равна:
![]() кН.
кН.
Проверим условие (72):
![]() кН,
кН,
т. е. прочность панели по поперечной силе обеспечена.
Расчет наклонных сечений
на действие изгибающего момента
Пример 21. Дано: свободно опертая железобетонная балка пролетом l =
5,5 м с равномерно распределенной
нагрузкой q = 29
кН/м; конструкция приопорного участка балки принята по черт. 30; бетон тяжелый класса В15 (Rb
= 7,7 МПа;
Rbt = 0,67 МПа при gb2 = 0,9); продольная арматура без анкеров класса А-III (Rs
= 365 МПа), площадью сечения As
= 982 мм2 (2 Æ 25) и ![]() =
226 мм2 (2 Æ 12); хомуты из арматуры класса А-I (Rsw = 175
МПа), диаметром 6 мм, шагом s = 150 мм
приварены к продольным стержням.
=
226 мм2 (2 Æ 12); хомуты из арматуры класса А-I (Rsw = 175
МПа), диаметром 6 мм, шагом s = 150 мм
приварены к продольным стержням.
Требуется проверить прочность наклонных сечений на действие изгибающего момента.
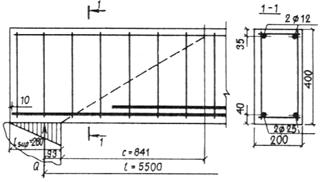
Черт. 30. К примеру расчета 21
Расчет. h0 = h – a = 400 – 40 = 360 мм. Поскольку растянутая арматура не имеет анкеров, расчет наклонных сечений на действие момента необходим.
Принимаем начало наклонного сечения у грани опоры. Отсюда lx = lsup – 10 мм = 280 – 10 = 270 мм (см. черт. 30).
По формуле (81) определим длину зоны анкеровки lan, принимая wan = 0,5 и Dlan = 8:
![]() мм.
мм.
Поскольку lx < lan, расчетное
сопротивление растянутой арматуры снижаем путем умножения его на коэффициент ![]() = 0,340, отсюда Rs = 365 · 0,340 = 124,1 МПа.
= 0,340, отсюда Rs = 365 · 0,340 = 124,1 МПа.
Поскольку к растянутым стержням в пределах длины lx приварены четыре вертикальных и два горизонтальных поперечных стержня (см. черт. 30), увеличим усилие RsAs = 124,1 · 982 = 121,9 · 103 H на величину Nw.
Принимая dw = 6 мм, nw = 6, jw = 200 (см. табл. 22), получим
![]() H.
H.
Отсюда RsAs = 121,9 + 20,26 = 142,2 кН.
Поскольку эта величина не превышает значения RsAs, определенного без учета gs5 и Nw, т. е. равного 365 · 982 = 358 · 103 H, оставляем RsAs = 142,2 кН.
Высоту сжатой зоны определим по формуле (16):
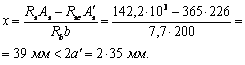
Согласно п. 3.42 принимаем zs = h0 – a’ = 360 – 35 = 325 мм.
По формуле (55) вычислим величину qsw:
![]() Н/мм.
Н/мм.
Определим
длину проекции невыгоднейшего наклонного сечения по формуле (83), принимав значение Q равным опорной реакции балки, т. е. Q = ![]() = 80
кН, а также Fi = 0 и
As,inc =0:
= 80
кН, а также Fi = 0 и
As,inc =0:
![]() мм.
мм.
Определим максимальную длину ls приопорного участка, за которым выполняется условие (72), с умножением правой части на 0,8 и при с = c1 £ 0,8cmax = 2h0, т. е. из решения уравнения
![]()
Предполагая, что ls > 2h0, принимаем максимальное значение c1 = 2h0. Тогда при jb4 =1,5 получим

Поскольку ls = 1760 мм > c = 821 мм, оставим с = 821 мм.
Момент внешних сил относительно оси, расположенной посредине высоты сжатой зоны наклонного сечения, в данном случае равен изгибающему моменту в нормальном сечении, проходящем через указанную ось, т. е. на расстоянии l1 + с = lsup/3 + с = 280/3 + 821 = 914 мм от точки приложения опорной реакции:
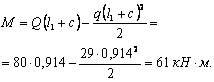
Проверим прочность из условия (77) с учетом формулы (78):
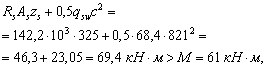
т. е. прочность наклонных сечений на действие изгибающего момента обеспечена.
Поскольку балка не имеет отгибов и нагружена равномерно распределенной нагрузкой, прочность наклонного сечения можно также проверить по более простой формуле (84), принимая М0 = Ql1 = 80 · 103 · 93 = 7,4 · 106 Н · мм:
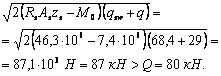
Пример 22. Дано: ригель многоэтажной рамы с эпюрами изгибающих моментов и поперечных сил от равномерно распределенной нагрузки q = 228 кН/м по черт. 31; бетон тяжелый класса В25; продольная и поперечная арматура класса А-III (Rs = 365 МПа; Rsw = 290 МПа); поперечное сечение приопорного участка — по черт. 31; хомуты диаметром 10 мм, шагом s = 150 мм (Аsw = 236 мм2).
Требуется определить расстояние от левой опоры до места обрыва первого стержня верхней арматуры.
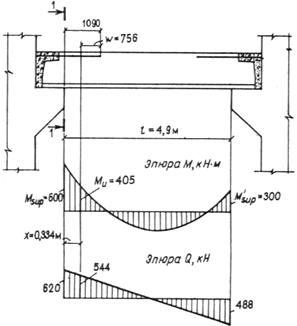
Черт. 31. К примеру расчета 22
Расчет.
Определим предельный изгибающий момент, растягивающий опорную арматуру без
учета обрываемого стержня, из условия (19), поскольку
Аs = 1609
мм2
< ![]() т. е.
х < 0:
т. е.
х < 0:
![]() кН · м.
кН · м.
По эпюре моментов определим расстояние х от опоры до места теоретического обрыва первого стержня из уравнения
![]()
откуда
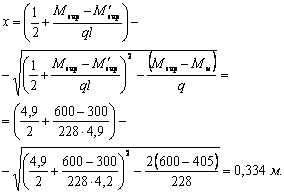
Поперечная сила в месте теоретического обрыва равна:
![]() кН.
кН.
Определим величину qsw:
![]() Н/мм.
Н/мм.
По формуле (87) вычислим длину w, на которую надо завести обрываемый стержень за точку теоретического обрыва:
![]() мм.
мм.
Следовательно, расстояние от опоры до места обрыва стержня может быть принято равным x + w = 334 + 756 = 1090 мм.
Определим необходимое расстояние 1an от места обрыва стержня до вертикального сечения, в котором он используется полностью, по табл. 45 :
![]() = 930 мм < 1090 мм.
= 930 мм < 1090 мм.
Следовательно, оборвем стержень на расстоянии 1090 мм от опоры.
Пример 23. Дано: примыкание сборной железобетонной балки перекрытия к ригелю с помощью подрезки, как показано на черт. 32, а; бетон тяжелый класса В25 (Rb = 13 МПа; Rbt = 0,95 МПа при gb2 = 0,9); хомуты и отогнутые стержни из арматуры класса А-III, диаметром соответственно 12 и 16 мм (Asw = 452 мм2; As,inc = 804 мм2); площадь сечения дополнительных хомутов у подрезки Asw1 = 402 мм2 (2 Æ 16); продольная арматура класса А-III по черт. 32, б; поперечная сила на опоре Q = 640 кН.
Требуется проверить прочность наклонных сечений.
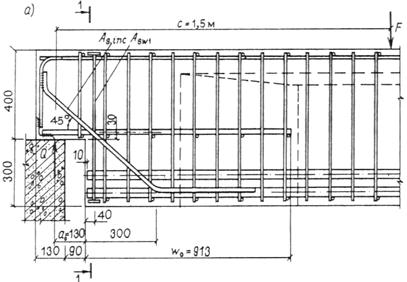
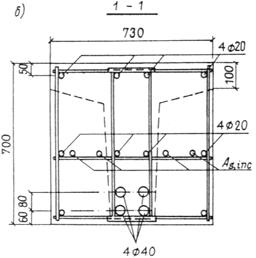
Черт. 32. К примеру расчета 23
Расчет. Проверим прочность наклонного сечения подрезки по поперечной силе согласно п. 3.31, принимая h0 = 370 мм, b = 730 мм (см. черт. 32), jb2 = 2 (см. табл. 21):
![]() Н · мм.
Н · мм.
При значении с, равном расстоянию от опоры до первого груза — с = 1,5 м, имеем

(jb3 = 0,6 — см. табл. 21),
следовательно, принимаем Qb = 154 · 103 H;
![]() Н/мм;
Н/мм;
![]()
при этом c0 < c = 1,5 м и c0 > h0.
Тогда Qb + qswc0 +RswAsw1 = 154 · 103 + 1152 · 406 + 290 · 402 = 738 · 103 H > Q = 640 кН, т.е. даже без учета отгибов прочность подрезки по поперечной силе обеспечена.
Проверим
достаточность .дополнительных хомутов и отгибов из условия (89). Из черт.
32 q = 45°; h0 = 700 – 60 – 80/2 = 600 мм; h01 = 370 мм; RswAsw1 + RswAs,inc sin45° = 290 · 402 + 290 ·804 · 0,707 = 281
· 103 H > Q ![]() = 640
= 640![]() = 245 кН.
= 245 кН.
Проверим прочность наклонного сечения, проходящего через входящий угол подрезки, на действие изгибающего момента.
Невыгоднейшее значение с определим по формуле (83), учитывая в числителе отгибы и дополнительные хомуты и принимая Fi = 0 и q = 0:
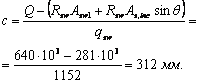
Поскольку продольная арматура короткой консоли заанкерена на опоре, учитываем эту арматуру с полным расчетным сопротивлением, т. е. с Rs = 365 МПа.
Из черт. 32 Аs = ![]() =
1256 мм2
(4 Æ 20). Поскольку As =
=
1256 мм2
(4 Æ 20). Поскольку As = ![]() x = 0,
тогда zs = h01 – а’ = 370 – 50 = 320 мм.
x = 0,
тогда zs = h01 – а’ = 370 – 50 = 320 мм.
Согласно формуле (79) принимая a1 = 30 мм, получим
![]() мм.
мм.
Проверим условие (77), принимая:

![]()
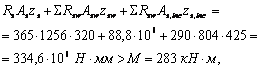
т. е. прочность наклонного сечения обеспечена.
Определим необходимую длину заведения продольной растянутой арматуры за конец подрезки по формуле (88):

Выясним необходимость постановки анкеров для нижней арматуры балки. Для этого проверим наклонное сечение, расположенное вне подрезки и начинающееся на расстоянии h0 – h01 = 600 — 370 = 230 мм от торца балки. Тогда lx = 230 – 10 = 220 мм.
Длину анкеровки для нижней арматуры определим по поз. 1 табл. 45, из которой при классе бетона В25 и классе арматуры А-III находим lan = 29, отсюда lan = 29 · 40 = 1160 мм > lx = 220 мм.
Расчетное
сопротивление нижней арматуры снизим умножением на коэффициент ![]() т. e. Rs = 365 · 0,19 = 69,2 МПа.
т. e. Rs = 365 · 0,19 = 69,2 МПа.
Из черт. 32 Аs = 5027 мм2 (4 Æ 40).
Учитывая, что в пределах длины lx = 220 м два верхних стержня имеют по два приваренных вертикальных стержня, а два нижних стержня имеют по два вертикальных и один горизонтальный приваренный стержень, увеличим усилие RsAs на величину Nw, определяемую по формуле (82), принимая nw = 10, dw = 12 мм, jw = 100 (см. табл. 22):
![]()
Отсюда
![]()
Принимая b = ![]() =
730 мм, определим высоту сжатой зоны х:
=
730 мм, определим высоту сжатой зоны х:
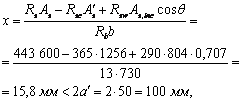
и, следовательно, zs = h0 – a’ = 600 —50 = 550 мм.
Невыгоднейшее значение с равно:
![]()
т. е. при таком значении с наклонное сечение пересекает продольную арматуру короткой консоли. Принимаем конец наклонного сечения в конце указанной арматуры, т. е. на расстоянии w0 — 953 мм от подрезки, при этом с = 723 мм. Расчетный момент М в сечении, проходящем через конец наклонного сечения, равен:
![]() кН · м;
кН · м;
![]() мм
мм
[где a1 = 300 – 230 = 70 мм (см. черт. 32)].
Проверим условие (77):
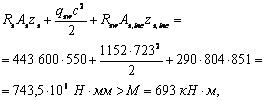
т. е. прочность наклонного сечения обеспечена, и, следовательно, анкера для нижней арматуры не требуются.
Проверим прочность короткой консоли подрезки согласно пп. 3.99 и 3.100 с учетом п. 3.31.
Проверим условие (207), принимая lsup = 130 мм, ax = 90 мм, h01 – a’ = 370 – 50 = 320 мм (см. черт. 32). Тогда
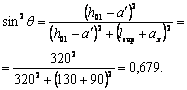
Принимая mw = 0 и заменяя 0,8 на 1,0, имеем Rbblsupsin2q = 13 · 730 ·130 · 0,679 = 838 · 103 H < 3,5Rbtbh01 = 3,5 · 0,95 · 730 · 370 = 898 · 103 H, т. е. правую часть условия (207) оставляем равной 838 кН.
Поскольку Q = 640 кН < 838 кН, прочность сжатой полосы обеспечена.
Проверим условие (208), принимая l1 = lsup + ax = 220 мм, h0 = 320 мм, As = 1256 мм2 (4 Æ 20):
![]()
т. е. продольной арматуры в короткой консоли поставлено достаточно.
Внецентренно сжатые элементы
ОБЩИЕ ПОЛОЖЕНИЯ
3.50 (1.21). При расчете внецентренно сжатых железобетонных элементов должен приниматься во внимание случайный эксцентриситет ea, обусловленный не учтенными в расчете факторами. Эксцентриситет ea в любом случае принимается не менее:
1/600 длины элемента или расстояния между его сечениями, закрепленными от смещения;
1/30 высоты сечения;
10 мм (для конструкций, образуемых из сборных элементов, при отсутствии других экспериментально обоснованных значений ea).
Для элементов статически неопределимых конструкций (в том числе для колонн каркасных зданий) значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения e0 принимается равным эксцентриситету, полученному из статического расчета конструкции, но не менее ea.
В элементах статически определимых конструкций (например, фахверковых стойках, стойках ЛЭП) эксцентриситет е0 находится как сумма эксцентриситетов — определяемого из статического расчета и случайного.
3.51. Расчет внецентренно сжатых элементов производят с учетом влияния прогиба элемента в плоскости эксцентриситета продольной силы (в плоскости изгиба) и в нормальной к ней плоскости. В последнем случае принимается, что продольная сила приложена с эксцентриситетом e0, равным случайному эксцентриситету ea (см. п. 3.50).
Влияние прогиба элемента учитывается согласно пп. 3.54 и 3.55.
Расчет из плоскости изгиба можно не производить, если гибкость элемента l0/i (для прямоугольных сечений — l0/h) в плоскости изгиба превышает гибкость в плоскости, нормальной к плоскости изгиба.
При наличии расчетных эксцентриситетов в двух направлениях, превышающих случайные эксцентриситеты ea, производится расчет на косое внецентренное сжатие (см. пп. 3.73—3.75).
3.52. Для часто встречающихся видов сжатых элементов (прямоугольного сечения; двутаврового сечения с симметрично расположенной арматурой; круглого и кольцевого сечений с арматурой, равномерно распределенной по окружности) расчет по прочности нормальных сечений производится согласно пп. 3.61—3.75.
Для других видов сечений и при произвольном расположении продольной арматуры расчет нормальных сечений производится по формулам общего случая расчета нормального сечения внецентренно сжатого элемента согласно п. 3.76. При расчете элементов с применением ЭВМ во всех случаях рекомендуется пользоваться указаниями п. 3.76.
Если
выполняется условие ![]() > 0,02Ab, в расчетных формулах
пп. 3.61—3.76 рекомендуется учитывать
уменьшение действительной площади бетона сжатой зоны на величину
> 0,02Ab, в расчетных формулах
пп. 3.61—3.76 рекомендуется учитывать
уменьшение действительной площади бетона сжатой зоны на величину ![]() .
.
3.53. Расчет по прочности наклонных сечений внецентренно сжатых элементов производится аналогично расчету изгибаемых элементов в соответствии с пп. 3.28—3.49. При этом значение Mb определяется по формуле
![]() (90)
(90)
где ![]() но не
более 0,5; значение Qb,min принимается равным jb3 (1 + jf + jn) Х Rbtbh0, а в формулах (72)—(76) коэффициент jb4 заменяется выражением jb4 (1 +
jn).
но не
более 0,5; значение Qb,min принимается равным jb3 (1 + jf + jn) Х Rbtbh0, а в формулах (72)—(76) коэффициент jb4 заменяется выражением jb4 (1 +
jn).
Суммарный коэффициент 1 + jf + jn принимается не более 1,5.
Влияние продольных сил не учитывается, если они создают изгибающие моменты, одинаковые по знаку с моментами от действия поперечной нагрузки. Для внецентренно сжатых элементов статически неопределимых конструкций, при статическом расчете которых принимается, что продольная сила располагается в центре тяжести сечения, допускается всегда учитывать влияние продольных сил.
При отсутствии в пределах пролета внецентренно сжатого элемента поперечной нагрузки расчет наклонных сечений по прочности допускается не производить, если нормальные трещины не образуются [т.е. если выполняется условие (233) с заменой Rbt,ser на Rbt].
УЧЕТ ВЛИЯНИЯ ПРОГИБА ЭЛЕМЕНТА
3.54 (3.24, 3.6). При расчете внецентренно сжатых элементов следует учитывать влияние прогиба на их несущую способность, как правило, путем расчета конструкций по деформированной схеме, принимая во внимание неупругие деформации бетона и арматуры и наличие трещин.
Допускается производить расчет конструкций по недеформированной схеме, учитывая влияние прогиба элемента путем умножения эксцентриситета e0 на коэффициент h, определяемый по формуле
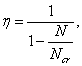 (91)
(91)
где Ncr — условная критическая сила, определяемая по формулам:
для элементов любой формы сечения
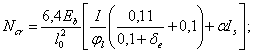 (92)
(92)
для элементов прямоугольного сечения
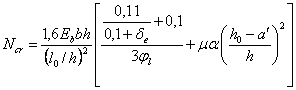 (93)
(93)
В формулах (92) и (93):
I, Is — моменты инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;
jl — коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии и равный:
![]() (94)
(94)
но не более 1 + b (здесь b — см. табл. 16);
M1, M1l — моменты внешних сил относительно оси, параллельной линии, ограничивающей сжатую зону и проходящей через центр наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры, соответственно от действия полной нагрузки и от действия постоянных и длительных нагрузок. Для элементов, рассчитываемых согласно пп. 3.61, 3.62, 3.65—3.68, допускается M1 и M1l определять относительно оси, проходящей через центр тяжести всей арматуры S. Если изгибающие моменты (или эксцентриситеты) от полной нагрузки и от суммы постоянных и длительных нагрузок имеют разные знаки, то при абсолютном значении эксцентриситета полной нагрузки e0 > 0,1h принимают jl = 1,0; если это условие не удовлетворяется, значение jl принимают равным jl = jl1 + 10(1 – jl1)е0/h, где jl1 определяют по формуле (94), принимая M1 равным произведению продольной силы N от действия полной нагрузки на расстояние от центра тяжести сечения до оси, проходящей через центр наиболее растянутого (наименее сжатого) от действия постоянных и длительных нагрузок стержня арматуры;
de — коэффициент, принимаемый равным e0/h, но не менее
![]() (95)
(95)
(здесь Rb — в МПа, допускается принимать при gb2 = 1,0; значение h для круглых и кольцевых сечений заменяется на D);
l0 — принимается в соответствии с п. 3.55;
![]() (96)
(96)
При расчете,
согласно п. 3.63, прямоугольных сечений с
арматурой, расположенной по высоте сечения, в значении Аs +
![]() не учитывается 2/3 арматуры, расположенной у граней,
параллельных плоскости изгиба (2Asl), а
значение
не учитывается 2/3 арматуры, расположенной у граней,
параллельных плоскости изгиба (2Asl), а
значение ![]() в формуле (93) принимается равным 1—2d1.
в формуле (93) принимается равным 1—2d1.
Для элементов из мелкозернистого бетона группы Б в формулы (92) и (93) вместо цифр 6,4 и 1,6 подставляются соответственно 5,6 и 1,4.
Эксцентриситет e0, используемый в настоящем пункте, допускается определять относительно центра тяжести бетонного сечения.
При гибкости элемента l0/i < 14 (для прямоугольных сечений — при l0/h < 4) принимается h =1.
При гибкости 14 £ l0/i < 35 (4 £ l0/h < 10) и при
![]() £ 0,025 допускается принимать:
£ 0,025 допускается принимать:
для прямоугольных сечений
![]()
для других форм сечения
![]()
При N > Ncr следует увеличивать размеры сечения.
При расчетных эксцентриситетах в двух направлениях коэффициент h допускается определять отдельно для каждого направления и умножать на соответствующий эксцентриситет.
3.55 (3.25). Расчетную длину l0 внецентренно сжатых железобетонных элементов рекомендуется определять как для элементов рамной конструкции с учетом ее деформированного состояния при наиболее невыгодном для данного элемента расположении нагрузки, принимая во внимание неупругие деформации материалов и наличие трещин.
Для элементов наиболее часто встречающихся конструкций допускается принимать расчетную длину l0 равной:
а) для колонн многоэтажных зданий при числе пролетов не менее двух и соединениях ригелей и колонн, рассчитываемых как жесткие, при конструкциях перекрытий:
сборных ..................... Н
монолитных ........ 0,7 Н
[где Н — высота этажа (расстояние между центрами узлов)];
б) для колонн одноэтажных зданий с шарнирным опиранием несущих конструкций покрытий, жестких в своей плоскости (способных передавать горизонтальные усилия), а также для эстакад — по табл. 23;
в) для элементов ферм и арок — по табл. 24.
Таблица 23 (32)
|
|
Расчетная длина l0 колонн одноэтажных зданий при расчете их в плоскости |
||||||
|
Характеристика зданий и колонн |
поперечной рамы или перпендикулярной |
перпендикулярной поперечной раме или параллельной оси эстакады |
|||||
|
|
к оси эстакады |
при наличии |
при отсутствии |
||||
|
|
|
связей в плоскости продольного ряда колонн или анкерных опор |
|||||
|
|
|
|
Подкрановая (нижняя) часть |
Разрезных |
1,5 Н1 |
0,8 Н1 |
1,2 Н1 |
|
|
|
При учете |
колонн при подкрановых балках |
Неразрезных |
1,2 Н1 |
0,8 Н1 |
0,8 Н1 |
|
|
|
нагрузки от кранов |
Надкрановая (верхняя) часть |
Разрезных |
2,0 Н2 |
1,5 Н2 |
2,0 Н2 |
|
|
С мостовыми |
|
колонн при подкрановых балках |
Неразрезных |
2,0 Н2 |
1,5 Н2 |
1,5 Н2 |
|
|
кранами |
|
Подкрановая (нижняя)часть |
Однопролетных |
1,5 Н |
0,8 Н1 |
1,2 Н |
|
|
|
Без учета |
колонн зданий |
Многопролетных |
1,2 Н |
0,8 Н1 |
1,2 Н |
|
Здания |
|
нагрузки от кранов |
Надкрановая (верхняя) часть |
Разрезных |
2,5 Н2 |
1,5 Н2 |
2,0 Н2 |
|
|
|
|
колонн при подкрановых балках |
Неразрезных |
2,0 Н2 |
1,5 Н2 |
1,5 Н2 |
|
|
|
|
Нижняя часть колонн |
Однопролетных |
1,5 Н |
0,8 Н |
1,2 Н |
|
|
|
Колонны |
зданий |
Многопролетных |
1,2 Н |
0,8 Н |
1,2 Н |
|
|
Без мостовых кранов |
ступенчатые |
Верхняя часть колон |
2,5 Н2 |
2,0 Н2 |
2,5 Н2 |
|
|
|
|
Колонны постоянного сечения |
Однопролетных |
1,5 Н |
0,8 Н |
1,2 Н |
|
|
|
|
зданий |
Многопролетных |
1,2 Н |
0,8 Н |
1,2 Н |
|
|
|
Крановые |
При подкрановых |
Разрезных |
2,0 Н1 |
0,8 Н1 |
1,5 Н1 |
|
|
Эстакады |
|
балках |
Неразрезных |
1,5 Н1 |
0,8 Н1 |
Н1 |
|
|
|
Под трубопроводы |
При соединении колонн |
Шарнирном |
2,0 Н |
Н |
2,0 Н |
|
|
|
|
с пролетным строением |
Жестком |
1,5 Н |
0,7 Н |
1,5 Н |
|
Обозначения, принятые в табл. 23:
Н — полная высота колонны от верха фундамента до горизонтальной конструкции (стропильной или подстропильной, распорки) в соответствующей плоскости;
H1 — высота подкрановой части колонны от верха фундамента до низа подкрановой балки;
H2 — высота надкрановой части колонны от ступени колонны до горизонтальной конструкции в соответствующей плоскости.
Примечание. При наличии связей до верха колони в зданиях с мостовыми кранами расчетная длина надкрановой части колонн в плоскости оси продольного ряда колонн принимается равной Н2.
Таблица 24 (33)
|
Элементы |
Расчетная длина l0 элементов ферм и арок |
|
1. Элементы ферм: а) верхний пояс при расчете: в плоскости фермы: при е0 < 1/8h1 |
0,9l |
|
„ e0 ³ 1/8h1 |
0,8l |
|
из плоскости фермы: для участка под фонарем (при ширине фонаря 12 м и более) |
0,8l |
|
в остальных случаях |
0,9l |
|
б) раскосы и стойки при расчете: в плоскости фермы |
0,8l |
|
из плоскости фермы: при b1/b2 < 1,5 |
0,9l |
|
„ b1/b2 ³ 1,5 |
0,8l |
|
2. Арки: а) при расчете в плоскости арки: трехшарнирной |
0,580L |
|
двухшарнирной |
0,540L |
|
бесшарнирной |
0,365L |
|
б) при расчете из плоскости арки (любой) |
L |
Обозначения, принятые в табл. 24:
l — длина элемента между центрами примыкающих узлов; для верхнего пояса фермы при расчете из плоскости фермы — расстояние между точками его закрепления;
L — длина арки вдоль ее геометрической оси; при расчете из плоскости арки — длина арки между точками ее закрепления из плоскости арки;
h1 — высота сечения верхнего пояса;
b1, b2 — ширина сечения соответственно верхнего пояса и стойки (раскоса) фермы.
3.56. Влияние прогибов колонн многоэтажных каркасных, зданий рекомендуется учитывать, принимая окончательные моменты М в опорных сечениях колонн равными:
![]() (97)
(97)
где Mv — момент от вертикальных нагрузок на перекрытиях;
hv — коэффициент, принимаемый равным единице, а в заделках в фундаменты определяемый по формуле (91) при l0 = 0,7H (Н — высота этажа) и при учете только вертикальных нагрузок;
Mh — момент от горизонтальных (ветровых, сейсмических) нагрузок;
hh — коэффициент h, определяемый согласно пп. 3.54 и 3.55 при учете всех нагрузок;
Мt — момент от вынужденных горизонтальных смещений (например, от температурных деформаций перекрытий, смещений жестких связевых диафрагм).
Моменты от всех нагрузок для сечений в средней трети длины колонн умножаются на коэффициент п, определенный согласно пп. 3.54 и 3.55, а моменты в прочих сечениях определяются линейной интерполяцией.
Значения моментов в опорных сечениях колонн, определенные по формуле (97), необходимо учитывать при определении моментов в примыкающих к колонне элементах (фундаментах, ригелях с жесткими узлами).
УЧЕТ ВЛИЯНИЯ КОСВЕННОГО АРМИРОВАНИЯ
3.57 (3.22). Расчет элементов сплошного сечения из тяжелого и мелкозернистого бетонов с косвенным армированием в виде сварных сеток, спиральной или кольцевой арматуры (черт. 33) следует производить согласно пп. 3.61—3.68, 3.71—3.76, вводя в расчет лишь часть площади бетонного сечения Aef, ограниченную осями крайних стержней сетки или спирали, и подставляя в расчетные формулы вместо Rb приведенную призменную прочность бетона Rb,red и вычисляя характеристику сжатой зоны бетона w с учетом влияния косвенного армирования по формуле (104).
Черт. 33. Сжатые элементы с косвенным армированием
а — в виде сварных сеток; б — в виде спиральной арматуры
Влияние прогиба элемента с косвенным армированием на эксцентриситет продольной силы учитывается согласно п. 3.58.
Гибкость l0/ief элементов с косвенным армированием не должна превышать:
при косвенном армировании сетками — 55 (для прямоугольных сечений — l0/hef £ 16);
при косвенном армировании спиралью — 35 (для круглых сечений — l0/def £ 9), где ief, hef, def —соответственно радиус инерции, высота и диаметр вводимой в расчет части сечения.
Значения Rb,red определяются по формулам:
а) при армировании сварными поперечными сетками
![]() (98)
(98)
где Rs,xy — расчетное сопротивление арматуры сеток;
![]() (99)
(99)
здесь пx, Asx, lx — соответственно число стержней, площадь поперечного сечения и длина стержня сетки (считая в осях крайних стержней) в одном направлении;
ny, Аsy, ly — то же, в другом направлении;
Aef — площадь сечения бетона, заключенного внутри контура сеток;
s — расстояние между сетками;
j — коэффициент эффективности косвенного армирования, определяемый по формуле
![]() (100)
(100)
![]() (101)
(101)
Rs,xy, Rb — в МПа.
Для элементов из мелкозернистого бетона значение коэффициента j следует принимать не более единицы;
б) при армировании спиральной или кольцевой арматурой
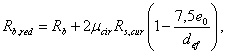 (102)
(102)
где Rs,cir — расчетное сопротивление арматуры спирали;
mcir — коэффициент армирования, равный:
![]() (103)
(103)
здесь Аs,cir — площадь поперечного сечения спиральной арматуры;
def — диаметр сечения внутри спирали;
s — шаг спирали;
e0 — эксцентриситет приложения продольной силы (без учета влияния прогиба).
Значения коэффициентов армирования, определяемые по формулам (99) и (103), для элементов из мелкозернистого бетона следует принимать не более 0,04.
При определении граничного значения относительной высоты сжатой зоны для сечений с косвенным армированием в формулу (14) вводится
![]() (104)
(104)
где a — коэффициент, принимаемый согласно указаниям п. 3.14;
d2 — коэффициент, равный 10m, но принимаемый не более 0,15 [здесь m — коэффициент армирования mxy или mcir, определяемый по формулам (99) и (103) соответственно для сеток и спиралей].
Косвенное армирование учитывается в расчете при условии, что несущая способность элемента, определенная согласно указаниям настоящего пункта (вводя в расчет Aef и Rb,red), превышает его несущую способность, определенную по полному сечению А и значению расчетного сопротивления бетона Rb без учета косвенной арматуры. Кроме того, косвенное армирование должно удовлетворять конструктивным требованиям пп. 5.78—5.80.
3.58 (3.22). При расчете элементов с косвенным армированием по недеформированной схеме влияние прогиба элемента на эксцентриситет продольной силы учитывается согласно пп. 3.54—3.56. При этом значение Ncr, полученное по формуле (92) или (93), умножается на коэффициент j1 = 0,25 + 0,05 l0/cef £ 1,0, а значение de,min вычисляется по формуле de,min = 0,5 + 0,01l0/cef(1,0 – 0,1 l0/cef) — 0,01 Rb, где cef — высота или диаметр учитываемой части сечения.
Кроме того, при вычислении Ncr размеры сечения принимаются по учитываемой части сечения.
3.59 (3.22). В элементах из тяжелого бетона с косвенным армированием в виде сеток рекомендуется применять продольную высокопрочную арматуру классов A-V и A-VI, используя ее повышенное (приведенное) расчетное сопротивление сжатию, равное:
![]() (105)
(105)
где l1, l2, Rsc, Rs — см. табл. 25;
![]()
здесь ![]() (106)
(106)
но не менее 1,0 и не более 1,6;
y, Aef — см. п. 3.57;
As,tot — площадь сечения всей продольной высокопрочной арматуры;
Rb — в МПа.
Таблица 25
|
Класс |
l1, l2 и Rsc, МПа, при коэффициенте gb2 (см. п. 3.1), равном |
Rs, МПа |
Rs,ser, МПа |
|||||
|
арматуры |
0,9 |
1,0 или 1,1 |
|
|
||||
|
|
l1 |
l2 |
Rsc |
l1 |
l2 |
Rsc |
|
|
|
A-V |
1,25 |
0,53 |
500 |
2,78 |
1,03 |
400 |
680 |
785 |
|
A-VI |
2,04 |
0,77 |
500 |
3,88 |
1,25 |
400 |
815 |
980 |
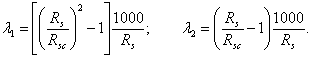
Значение ssc,u в формулах (14) и (155) принимается равным ssc,u = 380 + 1000d3, но не более 1200 МПа.
Указанные элементы прямоугольного сечения с арматурой, сосредоточенной у наиболее и наименее сжатых граней, рассчитываются согласно пп. 3.65 и 3.61, если высота сжатой зоны х, определенная по формуле (107а) или (110а), превышает граничное значение xRh0 при замене в расчетных формулах Rs на 0,8Rs. В противном случае расчет производится согласно п. 3.41 „Пособия по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов", принимая ssp = 0. В этом случае пpимeнeниe косвенного армирования и высокопрочной сжатой арматуры малоэффективно.
3.60 (3.23). При расчете внецентренно сжатых элементов с косвенным армированием наряду с расчетом по прочности согласно указаниям п. 3.57 следует производить расчет, обеспечивающий трещиностойкость защитного слоя бетона.
Расчет производится согласно указаниям пп. 3.61—3.68, 3.71—3.76 по эксплуатационным значениям расчетных нагрузок (gf = 1,0), учитывая всю площадь сечения бетона и принимая расчетные сопротивления Rb,ser и Rs,ser для предельных состояний второй группы и расчетное сопротивление арматуры сжатию равным значению Rs,ser, но не более 400 МПа.
При определении значения xR в формулах (14) и (155) принимают ssc,u = 400 МПа, а в формуле (15) коэффициент 0,008 заменяют на 0,006.
При учете влияния гибкости следует пользоваться указаниями п. 3.54, определяя значения de,min по формуле (95) с заменой 0,010Rb на 0,008Rb,ser.
РАСЧЕТ ЭЛЕМЕНТОВ СИММЕТРИЧНОГО СЕЧЕНИЯ
ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ СИММЕТРИИ
ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
С СИММЕТРИЧНОЙ АРМАТУРОЙ
3.61. Проверка прочности прямоугольных сечений с симметричной арматурой, сосредоточенной у наиболее сжатой и у растянутой (наименее сжатой) граней элемента, производится следующим образом в зависимости от высоты сжатой зоны х:
![]() (107)
(107)
а) при х £ xRh0 (черт. 34) — из условия
![]() (108)
(108)
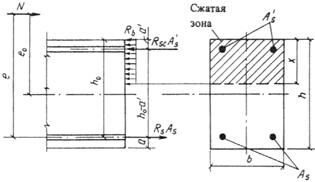
Черт. 34. Схема усилий в поперечном прямоугольном
сечении внецентренно сжатого элемента
б) при х > xRh0 — из условия (108), принимая высоту сжатой зоны равной х = xh0, где значение x определяется по формулам:
для элементов из бетона класса В30 и ниже
![]() (109)
(109)
для элементов из бетона класса выше В30
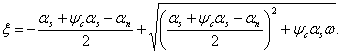 (110)
(110)
В формулах (109) и (110):
![]()
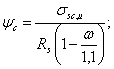
xR, yc, w — см. табл. 18 и 19.
Значение е вычисляется по формуле
![]() (111)
(111)
При этом эксцентриситет продольной силы e0 относительно центра тяжести сечения определяется с учетом прогиба элемента согласно пп. 3.54—3.56.
Примечания: 1. Если высота сжатой зоны, определенная с
учетом половины сжатой арматуры, ![]() расчетную несущую способность сечения можно несколько
увеличить, используя условие (108) при
расчетную несущую способность сечения можно несколько
увеличить, используя условие (108) при ![]() и
и ![]()
2. Формулой (110) можно пользоваться также при расчете элементов из бетона класса В30 и ниже.
3.62.
Требуемое количество симметричной арматуры определяется следующим образом в
зависимости от относительной величины продольной силы ![]()
а) при an £ xR
![]() (112)
(112)
б) при an > xR
![]() (113)
(113)
где x — относительная высота сжатой зоны определяемая по формуле (109) или (110).
Значение as в формуле (109) допускается определять по формуле
![]() (114)
(114)
а в формуле (110) — по формуле (114) с заменой an на (an + xR)/2.
В формулах (112)—(114):
![]()
Значение е вычисляется по формуле (111).
Если значение a’ не превышает 0,15h0, необходимое количество арматуры можно определять с помощью графика черт. 35, используя формулу
![]()
где as определяется по графику черт. 35 в зависимости от значений
![]() и
и ![]()
при этом значение момента М относительно центра тяжести сечения определяется с учетом прогиба элемента согласно пп. 3.54—3.56.

Черт. 35. Графики несущей способности внецентренно
сжатых элементов прямоугольного сечения с симметричной
арматурой
![]()
При статическом расчете по недеформированной схеме и при использовании коэффициента h > 1 подбор арматуры по приведенным формулам и графику черт. 35 производится в общем случае путем последовательных приближений.
Для элементов из тяжелого бетона классов В15—В50, а также из легкого бетона классов В10—В40 при марке по средней плотности не ниже D1800, при l = l0/h £ 25 и при а’ не более 0,15h0 подбор арматуры можно производить без последовательных приближений с помощью графиков прил. 3, при этом используются значения М без учета коэффициента h.
3.63. При наличии арматуры, расположенной по высоте сечения, расчет внецентренно сжатых элементов допускается производить по формулам (117) и (118), рассматривая всю арматуру как равномерно распределенную по линиям центров тяжести стержней (черт. 36). При этом площадь сечения арматуры Asl, расположенной у одной из граней, параллельных плоскости изгиба, принимается равной:
![]() (115)
(115)
где Аs1,l — площадь одного промежуточного стержня; при разных диаметрах принимается средняя площадь сечения стержня;
nl — число промежуточных стержней.
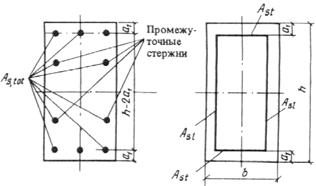
Черт. 36. Схема, принимаемая при расчете внецентренно
сжатого элемента прямоугольного сечения с арматурой,
расположенной по высоте сечения
Площадь сечения арматуры Ast, расположенной у одной из граней, перпендикулярных плоскости изгиба, равна:
![]() (116)
(116)
где Аs,tot — площадь всей арматуры в сечении элемента.
Проверка
прочности сечения производится в зависимости от относительной высоты сжатой
зоны ![]()
а) при x £ xR прочность сечения проверяется из условия
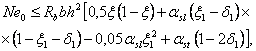 (117)
(117)
где ![]()
![]()
(см. черт. 36);
б) при x > xR прочность сечения проверяется из условия
![]() (118)
(118)
где ![]() — относительная величина продольной силы при
равномерном сжатии всего сечения;
— относительная величина продольной силы при
равномерном сжатии всего сечения;
amR, anR — относительные величины соответственно изгибающего момента и продольной силы при высоте сжатой зоны xR h, равные:
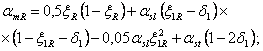
![]()
![]() xR, w — см. табл. 18 и 19.
xR, w — см. табл. 18 и 19.
Эксцентриситет продольной силы е0 определяется с учетом прогиба элемента согласно пп. 3.54—3.56.
Примечание. При расположении арматуры в пределах крайних четвертей высоты h — 2a1 (см. черт. 36) расчет производится согласно пп. 3.61 и 3.62, рассматривая арматуру S и S’ сосредоточенной по линиям их центров тяжести.
3.64. Расчет сжатых элементов из тяжелого бетона классов В15—В40 или из легкого бетона классов B12,5—В30 и марок по средней плотности не ниже D1800 на действие продольной силы, приложенной с эксцентриситетом, принятым, согласно п. 3.50, равным случайному эксцентриситету ea = h/30, при l0 £ 20h допускается производить из условия
![]() (119)
(119)
где j — коэффициент, определяемый по формуле
![]() (120)
(120)
но принимаемый не более jsb,
здесь jb, jsb — коэффициенты, принимаемые по табл. 26 и 27;
Таблица 26
|
Бетон |
|
Коэффициент jb при l0/h |
|||||||
|
|
|
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
Тяжелый |
0 |
0,93 |
0,92 |
0,91 |
0,90 |
0,89 |
0,88 |
0,86 |
0,84 |
|
|
0,5 |
0,92 |
0,91 |
0,90 |
0,89 |
0,86 |
0,82 |
0,78 |
0,72 |
|
|
1,0 |
0,92 |
0,91 |
0,89 |
0,86 |
0,82 |
0,76 |
0,69 |
0,61 |
|
Легкий |
0 |
0,92 |
0,91 |
0,90 |
0,88 |
0,86 |
0,82 |
0,77 |
0,72 |
|
|
0,5 |
0,92 |
0,90 |
0,88 |
0,84 |
0,79 |
0,72 |
0,64 |
0,55 |
|
|
1,0 |
0,91 |
0,90 |
0,86 |
0,80 |
0,71 |
0,62 |
0,54 |
0,45 |
Таблица 27
|
Бетон |
|
Коэффициент jb при l0/h |
|||||||
|
|
|
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
А. При а = a’ < 0,15h и при отсутствии промежуточных стержней (см. эскиз) или при площади сечения этих стержней менее As,tot/3
|
|||||||||
|
Тяжелый |
0 |
0,93 |
0,92 |
0,91 |
0,90 |
0,89 |
0,88 |
0,86 |
0,84 |
|
|
0,5 |
0,92 |
0,92 |
0,91 |
0,89 |
0,88 |
0,86 |
0,83 |
0,79 |
|
|
1,0 |
0,92
|
0,91 |
0,90 |
0,89 |
0,87 |
0,84 |
0,79 |
0,74 |
|
Легкий |
0 |
0,92 |
0,92 |
0,91 |
0,89 |
0,88 |
0,85 |
0,82 |
0,77 |
|
|
0,5 |
0,92 |
0,91 |
0,90 |
0,88 |
0,86 |
0,83 |
0,77 |
0,71 |
|
|
1,0 |
0,92 |
0,91 |
0,90 |
0,88 |
0,85 |
0,80 |
0,74 |
0,67 |
|
Б. При 0,25h > a = a’ ³ 0,15h или при площади сечения промежуточных стержней (см. эскиз), равной или более As,tot/3, независимо от величины а
|
|||||||||
|
Тяжелый |
0 |
0,92 |
0,92 |
0,91 |
0,89 |
0.87 |
0,85 |
0,82 |
0,79 |
|
|
0,5 |
0,92 |
0,91 |
0,90 |
0,88 |
0,85 |
0,81 |
0,76 |
0,71 |
|
|
1,0
|
0,92 |
0,91 |
0,89 |
0,86 |
0,82 |
0,77 |
0,70 |
0,63 |
|
Легкий |
0 |
0,92 |
0,91 |
0,90 |
0,88 |
0,85 |
0,81 |
0,76 |
0,69 |
|
|
0,5 |
0,92 |
0,91 |
0,89 |
0,86 |
0,81 |
0,73 |
0,65 |
0,57 |
|
|
1,0
|
0,91 |
0,90 |
0,88 |
0,84 |
0,76 |
0,68 |
0,60 |
0,52 |
Обозначения, принятые в табл. 26 и 27:
Nl — продольная сила от действия постоянных и длительных нагрузок;
N — продольная сила от действия всех нагрузок
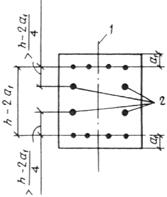
1 — рассматриваемая плоскость;
2 — промежуточные стержни
![]()
Аs,tot — см. п. 3.63;
при as > 0,5 можно, не пользуясь формулой (120), принимать j = jsb.
ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
С НЕСИММЕТРИЧНОЙ АРМАТУРОЙ
3.65. Проверка прочности прямоугольных сечений с несимметричной арматурой, сосредоточенной у наиболее сжатой и растянутой (наименее сжатой) граней элемента, производится согласно п. 3.61, при этом формулы (107), (109) и (110) приобретут вид:
![]() (107a)
(107a)
![]() (109a)
(109a)
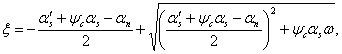 (110a)
(110a)
где ![]()
3.66. Площади сечений сжатой и растянутой арматуры, соответствующие минимуму их суммы, определяются по формулам:
для элементов из бетона класса В30 и ниже:
![]() (121)
(121)
![]() (122)
(122)
для элементов из бетона класса выше В30:
![]() (123)
(123)
![]() (124)
(124)
где aR, xR — определяются по табл. 18 и 19 и принимаются соответственно не более 0,4 и 0,55.
При отрицательном значении Аs, вычисленном по формуле (122) или (124), площадь сечения арматуры S принимается минимальной из конструктивных требований, но не менее величины
![]() (125)
(125)
а площадь сечения арматуры S определяется:
при отрицательном значении As,min — по формуле
 (126)
(126)
при положительном значении As,min — по формуле
![]() (127)
(127)
Если принятая
площадь сечения сжатой арматуры ![]() значительно превышает
ее значение, вычисленное по формуле (121)
или (123) (например, при отрицательном
значении
значительно превышает
ее значение, вычисленное по формуле (121)
или (123) (например, при отрицательном
значении ![]() ), площадь сечения
растянутой арматуры может быть уменьшена исходя из формулы
), площадь сечения
растянутой арматуры может быть уменьшена исходя из формулы
![]() (128)
(128)
где x — определяется по табл. 20 в зависимости от значения
![]() (129)
(129)
Если сжатая арматура отсутствует или не учитывается в расчете, площадь сечения растянутой арматуры определяется всегда только по формуле (128), при этом должно удовлетворяться условие am < aR.
ДВУТАВРОВЫЕ СЕЧЕНИЯ
С СИММЕТРИЧНОЙ АРМАТУРОЙ
3.67. Проверка прочности двутавровых сечений с симметричной арматурой, сосредоточенной в полках (черт. 37), производится следующим образом.
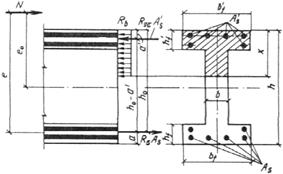
Черт. 37. Схема усилий в поперечном двутавровом сечении
внецентренно сжатого элемента
Если соблюдается условие
![]() (130)
(130)
(т. е. граница сжатой зоны
проходит в полке), расчет производится
как для прямоугольного сечения шириной ![]() в
соответствии с п. 3.61.
в
соответствии с п. 3.61.
Если условие (130) не соблюдается (т. е. граница сжатой
зоны проходит в ребре), расчет производится
в зависимости от высоты сжатой зоны ![]()
а) при х £ xR h0 прочность сечения проверяется из условия
![]() (131)
(131)
б) при х > xR h0 прочность сечения проверяется из условия (131), определяя высоту сжатой зоны по формуле
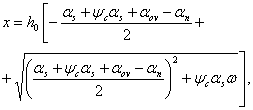 (132)
(132)
где ![]()
yc, xR, w — см. табл. 18 и 19;
Аov —
площадь сжатых свесов полки, равная ![]()
Если значение х, определенное по формуле (132), превышает h – hf (т. е.
граница сжатой зоны проходит по менее сжатой полке), можно учесть повышение несущей способности сечения за счет
включения в работу менее сжатой полки. Расчет при этом (если ![]() = bf) производится по
формулам (131) и (132) с заменой b на
= bf) производится по
формулам (131) и (132) с заменой b на ![]() ,
, ![]() на (h +
на (h + ![]() – hf),
принимая Aov = – (bf – b)
(h –
– hf),
принимая Aov = – (bf – b)
(h –![]() – hf).
– hf).
Примечание. При переменной
высоте свесов полок значения hf и ![]() принимаются равными средней высоте свесов.
принимаются равными средней высоте свесов.
3.68. Требуемое количество симметричной арматуры двутавровых сечений определяется следующим образом.
При соблюдении
условия (130) подбор арматуры
производится как для прямоугольного сечения шириной ![]() согласно п. 3.62.
согласно п. 3.62.
Если условие (130) не соблюдается, подбор арматуры производится в зависимости от относительной высоты сжатой зоны x:
![]() (133)
(133)
а) при x £ xR
![]() (134)
(134)
б) при x > xR
![]() (135)
(135)
где относительная высота сжатой зоны x1 = x/h0 определяется из формулы (132), принимая
![]() (136)
(136)
В формулах (133)—(136):
an, aov — см. п. 3.67;
![]()
![]()
КОЛЬЦЕВЫЕ СЕЧЕНИЯ
3.69. Проверка прочности кольцевых сечений (черт. 38) при соотношении внутреннего и наружного радиусов r1/r2 ³ 0,5 и арматуре, равномерно распределенной по окружности (при продольных стержнях не менее 6), производится следующим образом в зависимости от относительной площади сжатой зоны бетона xcir.
![]() (137)
(137)
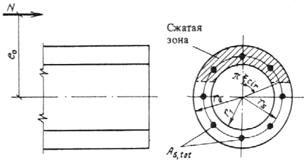
Черт. 38. Схема, принимаемая при расчете кольцевого
сечения внецентренно сжатого элемента
а) при 0,15 < xcir < 0,6 — из условия
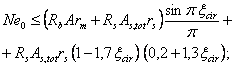 (138)
(138)
б) при xcir £ 0,15 — из условия
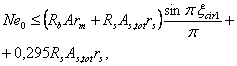 (139)
(139)
где ![]() (140)
(140)
в) при xcir ³ 0,6 — из условия
![]() (141)
(141)
где ![]() (142)
(142)
В формулах (137)—(142):
As,tot — площадь сечения всей продольной арматуры;
![]()
rs — радиус окружности, проходящей через центры тяжести стержней рассматриваемой арматуры.
Эксцентриситет продольной силы e0 определяется с учетом прогиба элемента согласно пп. 3.54—3.56.
3.70. Проверку прочности, а также определение необходимого количества продольной арматуры для кольцевых сечений, указанных в п. 3.69, при rs » rm допускается производить с помощью графиков черт. 39, используя формулы:
![]() (143)
(143)
![]() (144)
(144)
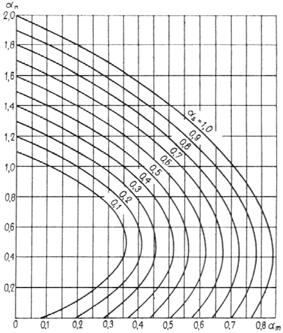
Черт. 39. Графики несущей способности внецентренно
сжатых элементов кольцевого сечения
![]()
где значения am и as определяются по
графику в зависимости от
значений соответственно ![]() и
и ![]() а также
а также ![]() . При этом эксцентриситет е0
определяется с учетом прогиба
элемента согласно пп. 3.54—3.56.
. При этом эксцентриситет е0
определяется с учетом прогиба
элемента согласно пп. 3.54—3.56.
КРУГЛЫЕ СЕЧЕНИЯ
3.71. Прочность круглых сечений (черт. 40) с арматурой, равномерно распределенной по окружности (при числе продольных стержней не менее 6) , при классе бетона не выше В30 проверяется из условия
![]() (145)
(145)
где r — радиус поперечного сечения;
xcir — относительная площадь сжатой зоны бетона, определяемая следующим образом:
при выполнении условия
![]() (146)
(146)
из решения уравнения
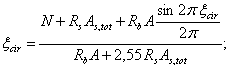 (147)
(147)
при невыполнении условия (146) — из решения уравнения
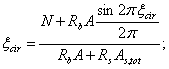 (148)
(148)
j — коэффициент, учитывающий работу растянутой арматуры и принимаемый равным: при выполнении условия (146) j = 1,6 (1 – 1,55 xcir) xcir, но не более единицы; при невыполнении условия (146) j = 0;
As,tot — площадь сечения всей продольной арматуры;
rs — радиус окружности, проходящей через центры тяжести стержней продольной арматуры.
Эксцентриситет продольной силы е0 определяется с учетом прогиба элемента согласно пп. 3.54—3.56.
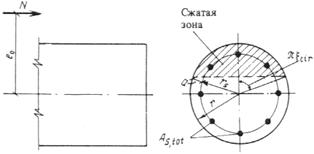
Черт. 40. Схема, принимаемая при расчете круглого сечения
внецентренно сжатого элемента
3.72. Проверку прочности, а также определение необходимого количества продольной арматуры для круглых сечений, указанных в п. 3.71, допускается производить с помощью графиков черт. 41, используя формулы:
![]() (149)
(149)
![]() (150)
(150)
где значения am и as определяются по
черт. 41 в зависимости от значений соответственно ![]() и
и
![]() а также
а также ![]() При этом
эксцентриситет е0 определяется с учетом прогиба элемента согласно пп. 3.54—3.56.
При этом
эксцентриситет е0 определяется с учетом прогиба элемента согласно пп. 3.54—3.56.
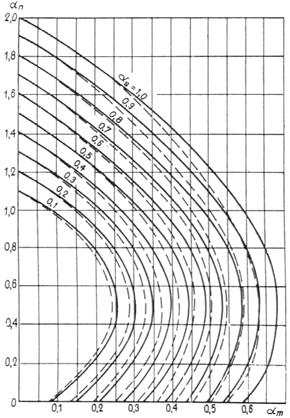
Условные обозначения:
——— при a/D = 0,05;
--------- при а/D = 0,10 .
Черт. 41. Графики несущей способности внецентренно
сжатых элементов круглого сечения
![]()
РАСЧЕТ ЭЛЕМЕНТОВ, РАБОТАЮЩИХ
НА КОСОЕ ВНЕЦЕНТРЕННОЕ СЖАТИЕ
3.73. Расчет нормальных сечений элементов, работающих на косое внецентренное сжатие, производится в общем случае согласно п. 3.76, определяя положение прямой, ограничивающей сжатую зону, с помощью последовательных приближений.
3.74. Расчет элементов прямоугольного сечения с симметричной арматурой на косое внецентренное сжатие допускается производить с помощью графиков черт. 42.
Прочность
сечения считается обеспеченной, если точки с координатами ![]() и
и
![]() на
графике, отвечающем параметру as, находятся внутри области, ограниченной
кривой, отвечающей параметру an1, и осями координат.
на
графике, отвечающем параметру as, находятся внутри области, ограниченной
кривой, отвечающей параметру an1, и осями координат.
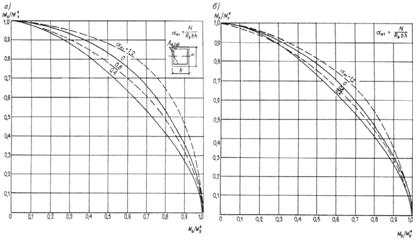
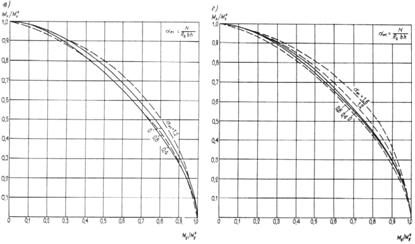
Черт. 42. Графики несущей способности элементов прямоугольного
сечения с симметричной арматурой, работающих
на косое внецентренное сжатие
a — при as = 0,2; б — при as = 0,4; в — при as = 0,6;
г — при as = 1,0 ![]()
Значения Мx и My представляют собой изгибающие моменты от внешней нагрузки относительно центра тяжести сечения, действующие соответственно в плоскостях симметрии х и у. Влияние прогиба элемента учитывается умножением моментов Мx и My на коэффициенты hx и hy, определяемые соответственно для плоскостей х и у согласно п. 3.54 при действующей продольной силе N.
Значения ![]() и
и ![]() представляют собой
предельные изгибающие моменты, которые могут восприниматься сечением в
плоскостях симметрии х и у с учетом действующей продольной силы N,
приложенной в центре тяжести сечения.
представляют собой
предельные изгибающие моменты, которые могут восприниматься сечением в
плоскостях симметрии х и у с учетом действующей продольной силы N,
приложенной в центре тяжести сечения.
Величины
предельных моментов ![]() и
и ![]() представляют собой
правые части условий (117) и (118). При этом дискретно расположенные стержни
арматуры заменяются распределенным армированием.
представляют собой
правые части условий (117) и (118). При этом дискретно расположенные стержни
арматуры заменяются распределенным армированием.
![]() (151)
(151)
![]() (152)
(152)
где Asx, Asy — площадь арматуры, расположенной у граней, нормальных соответственно к осям симметрии х и у (черт. 43),
Аs1,x, As1,y — площадь каждого из промежуточных стержней, расположенных у граней, нормальных соответственно к осям симметрии х и у;
nx — число промежуточных стержней площадью Аs1,x, расположенных по одной стороне сечения;
As0 — площадь углового стержня;
![]()
hx, hy — высота сечения при внецентренном сжатии соответственно в плоскостях х и у;
As,tot — площадь сечения всей продольной арматуры.
Параметры as и an1 определяются по формулам:
![]()
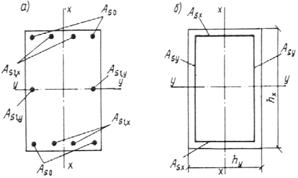
Черт. 43. Схемы расположения арматуры в прямоугольном
сечении при расчете на косое внецентренное сжатие
а — фактическая; б — расчетная
3.75. Расчет элементов симметричного двутаврового сечения при bf/b = 3—5 и hf/h = 0,15—0,25 с симметричной арматурой, расположенной в полках сечения, на косое внецентренное сжатие допускается производить с помощью графиков несущей способности, представленных на черт. 44.
Расчет производится аналогично расчету, приведенному в п. 3.74 для элементов прямоугольного сечения.
Предельный
момент ![]() , воспринимаемый сечением
в плоскости оси симметрии х,
проходящей в ребре, представляет собой правую часть условия (131), уменьшенную на N (h0 – a’)/2, а предельный момент
, воспринимаемый сечением
в плоскости оси симметрии х,
проходящей в ребре, представляет собой правую часть условия (131), уменьшенную на N (h0 – a’)/2, а предельный момент ![]() во взаимно
перпендикулярной плоскости симметрии у
допускается определять как для прямоугольного сечения, составленного из двух
полок, согласно п. 3.63.
во взаимно
перпендикулярной плоскости симметрии у
допускается определять как для прямоугольного сечения, составленного из двух
полок, согласно п. 3.63.
ОБЩИЙ СЛУЧАЙ РАСЧЕТА НОРМАЛЬНЫХ СЕЧЕНИЙ
ВНЕЦЕНТРЕННО СЖАТОГО ЭЛЕМЕНТА
(ПРИ ЛЮБЫХ СЕЧЕНИЯХ, ВНЕШНИХ УСИЛИЯХ
И ЛЮБОМ АРМИРОВАНИИ)
3.76 (3.28). Расчет сечений внецентренно сжатого элемента в общем случае (черт. 45) должен производиться из условия
![]() (153)
(153)
где ![]() —
расстояние продольной силы N до оси, параллельной прямой, ограничивающей сжатую зону,
и проходящей через центр тяжести сечения растянутого стержня, наиболее удаленного
от указанной прямой;
—
расстояние продольной силы N до оси, параллельной прямой, ограничивающей сжатую зону,
и проходящей через центр тяжести сечения растянутого стержня, наиболее удаленного
от указанной прямой;
Sb — статический момент площади сечения сжатой зоны бетона относительно указанной оси;
Ssi — статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;
ssi — напряжение в i-м стержне продольной арматуры, определяемое согласно указаниям настоящего пункта.
Высота сжатой зоны х и напряжения ssi определяются из совместного решения уравнений:
![]() (154)
(154)
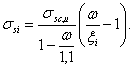 (155)
(155)
В формулах (154) и (155):
Asi — площадь сечения i-го стержня продольной арматуры;
xi —
относительная высота сжатой зоны бетона, равная
![]() где h0i —
расстояние от оси, проходящей
через центр тяжести сечения рассматриваемого i-го
стержня и параллельной прямой, ограничивающей сжатую зону, до наиболее
удаленной точки сжатой зоны сечения (см. черт.
45);
где h0i —
расстояние от оси, проходящей
через центр тяжести сечения рассматриваемого i-го
стержня и параллельной прямой, ограничивающей сжатую зону, до наиболее
удаленной точки сжатой зоны сечения (см. черт.
45);
w — характеристика сжатой зоны бетона, определяемая по формулам (15) или (104);
ssc,u — см. пп. 3.14 и 3.59.
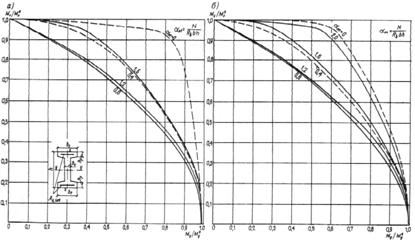
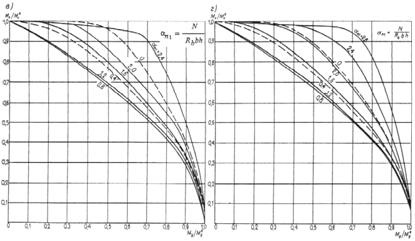
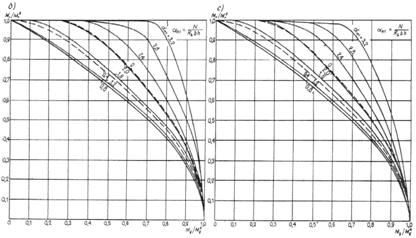
Черт. 44. Графики несущей способности элементов
симметричного двутаврового сечения, работающих
на косое внецентренное сжатие
а — при as = 0,2; б — при as = 0,6; в — при as = 1,0;
г — при as = 1,4 ![]()
д — при as = 1,8; е — при as = 2,8 ![]()
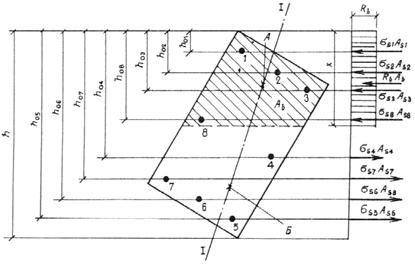
Черт. 45. Схема усилий и эпюра напряжении в сечении,
нормальном к продольной оси железобетонного элемента,
в общем случае расчета по прочности
I – I — плоскость, параллельная плоскости действия изгибающего момента,
или плоскость, проходящая через точки приложения продольной силы
и равнодействующих внутренних сжимающих и растягивающих усилий;
А — точка приложения равнодействующих усилий в сжатой арматуре
и в бетоне сжатой зоны; Б — то же, в растянутой арматуре;
1 – 8 — стержни
Напряжение ssi вводится в расчетные формулы со своим знаком, полученным при расчете по формуле (155), при этом напряжения со знаком „плюс" означают растягивающие напряжения и принимаются не более Rsi, а напряжения со знаком „минус" — сжимающие напряжения и принимаются по абсолютной величине не более Rsc.
Для определения положения границы сжатой зоны при косом внецентренном сжатии кроме использования формул (154) и (155) требуется соблюдение дополнительного условия: точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре должны лежать на одной прямой (см. черт. 45) .
Если в сечении
можно выявить характерную ось (например, ось симметрии или ось ребра
Г-образного сечения), при косом
внецентренном сжатии вместо соблюдения вышеуказанного дополнительного условия
рекомендуется производить расчет из
двух условий: из условия (153), определяя
значения ![]() , Sb и Ssi относительно оси х, проходящей через центр наиболее
растянутого стержня параллельно указанной характерной оси, и из того же условия (153), определяя значения
, Sb и Ssi относительно оси х, проходящей через центр наиболее
растянутого стержня параллельно указанной характерной оси, и из того же условия (153), определяя значения ![]() , Sb и Ssi относительно оси у, пересекающей под прямым утлом ось х в центре наиболее растянутого стержня.
При этом положение прямой, ограничивающей сжатую зону, подбирается
последовательными приближениями из уравнений
(154) и (155), принимая угол
наклона этой прямой q
постоянным и равным углу наклона нейтральной оси, определенному как для
упругого материала.
, Sb и Ssi относительно оси у, пересекающей под прямым утлом ось х в центре наиболее растянутого стержня.
При этом положение прямой, ограничивающей сжатую зону, подбирается
последовательными приближениями из уравнений
(154) и (155), принимая угол
наклона этой прямой q
постоянным и равным углу наклона нейтральной оси, определенному как для
упругого материала.
Прочность сечения будет обеспечена лишь при соблюдении условия (153) относительно обеих осей (х и у). Если при обеих проверках условие (153) не соблюдается, прочность не обеспечена и следует увеличить армирование, размеры сечения или повысить класс бетона. Если условие соблюдается только относительно одной оси, следует снова определить очертание сжатой зоны при другом угле q и произвести повторно аналогичный расчет.
ПРИМЕРЫ РАСЧЕТА
ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
С СИММЕТРИЧНОЙ АРМАТУРОЙ
Пример 24. Дано: колонна рамного каркаса с сечением размерами b = 400
мм, h = 500
мм; а
= a’ = 40 мм; бетон тяжелый класса В25 (Eb = 2,7 · 104 МПа); арматура
класса A-III (Rs = Rsc = 365
МПа; Еs = 2 · 105 МПа); площадь ее сечения Аs = ![]() =
1232 мм2 (2 Æ 28); продольные силы и изгибающие моменты: от
постоянных и длительных нагрузок Nl = 650 кН, Мl = 140 кН·м;
от ветровой нагрузки Nsh = 50 кН, Мsh = 73 кН·м;
расчетная длина колонны l0 = 6 м.
=
1232 мм2 (2 Æ 28); продольные силы и изгибающие моменты: от
постоянных и длительных нагрузок Nl = 650 кН, Мl = 140 кН·м;
от ветровой нагрузки Nsh = 50 кН, Мsh = 73 кН·м;
расчетная длина колонны l0 = 6 м.
Требуется проверить прочность сечения колонны.
Расчет. h0 = 500 – 40 = 460 мм. Поскольку имеют место усилия от нагрузки непродолжительного действия (ветровой), согласно п. 3.1 установим необходимость расчета по случаю „а".
Усилия от всех нагрузок равны:
N = 650 + 50 = 700 кН; М = 140 + 73 = 213 кН·м.
Определим моменты внешних сил относительно растянутой арматуры МI и МII, подсчитанные соответственно с учетом и без учета нагрузки непродолжительного действия (ветровой):
![]() кН·м;
кН·м;
![]() кН·м.
кН·м.
Так как 0,82MII = 0,82·360 = 295 кН·м > МI = 276,5 кН·м, производим расчет только по случаю „б" (см. п. 3.1), т. е. на действие всех нагрузок, принимая Rb = 16 МПа (при gb2 = 1,1).
Так как l0/h = 6/0,5 = 12 > 10, расчет производим с учетом прогиба колонны согласно п. 3.54, вычислялось по формуле (93).
Для этого определим:
![]()
[здесь b = 1,0 для тяжелого бетона (см. табл. 16)];
![]()
![]()
следовательно, случайный эксцентриситет не учитываем.
Так как
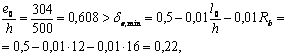
принимаем ![]()

Коэффициент h определим по формуле (91):

Значение е равно:
![]()
Определим высоту сжатой зоны х по формуле (107):
![]() мм.
мм.
xR = 0,55 (см. табл. 18).
Так как х = 109,4 мм < xRh0 = 0,55 · 460 = 253 мм, прочность сечения проверим из условия (108):
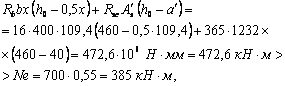
т. е. прочность сечения обеспечена.
Пример 25. Дано: сечение элемента размерами b = 400 мм, h = 500 мм; a = a' = 40 мм; бетон тяжелый класса В25 (Eb = 2,7 · 104 МПа); арматура симметричная класса A-III (Rs = Rsc = 365 МПа; Es = 2 · 105 МПа); продольные силы и изгибающие моменты: от постоянных и длительных нагрузок Nl = 600 кН, Ml = 170 кН·м; от ветровой нагрузки Nsh = 200 кН, Мsh = 110 кН·м; расчетная длина l0 = 8 м.
Требуется определить площадь сечения арматуры.
Расчет. h0 = 500 – 40 = 460 мм. Поскольку имеется усилие от ветровой нагрузки, проверим условие (1). Для этого вычислим:
![]() кН·м;
кН·м;
![]() кН·м;
кН·м;
![]() кН;
кН;
![]() кН·м.
кН·м.
Так как 0,82 MII = 0,82 · 448 = 368 кН·м > MI = 296 кН·м, расчет производим только по случаю „б", т. е. на действие всех нагрузок, принимая Rb = 16 МПа (при gb2 = 1,1).
Так как l0/h = 8000/500 = 16 > 10, расчет производим с учетом прогиба элемента согласно п. 3.54, вычисляя Ncr по формуле (93).
Для этого определим:
![]()
[b = 1,0, см. табл. 16];
![]()
(см. п. 3.50).
Так как е0/h = 350/500 = 0,7 > de,min = 0,5 – 0,01 ![]() – 0,01Rb,
принимаем de =
– 0,01Rb,
принимаем de = ![]() = 0,7.
= 0,7.
В первом
приближении принимаем m = 0,01, ![]() = 7,4,
= 7,4,
тогда

Коэффициент h равен:
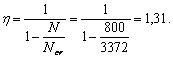
Значение е с учетом прогиба элемента равно:
![]() мм.
мм.
Необходимое армирование определим согласно п. 3.62.
Вычислим значения:
![]()
![]()
![]()
Из табл. 18 находим xR = 0,55.
Так как an < xR ,
значение Аs = ![]() определим по формуле (112):
определим по формуле (112):
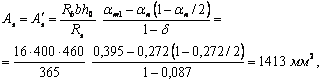
откуда
![]()
Поскольку полученное армирование существенно превышает армирование, принятое при определении Ncr (m = 0,01), значение Аs = 1413 мм2 определено с „запасом", и его можно несколько уменьшить, уточнив значение m.
Принимаем m = (0,01 + 0,014)/2 = 0,012 и аналогично вычислим значение Аs = ![]() :
:
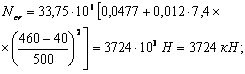
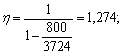
![]() мм;
мм;
![]()
![]() мм2.
мм2.
Окончательно
принимаем As = ![]() =
1362 мм2 (2 Æ 25 + 1 Æ 22).
=
1362 мм2 (2 Æ 25 + 1 Æ 22).
Пример 26. По данным примера 25 требуется определить площадь арматуры, используя графики прил. 3.
Расчет. В
соответствии с примером 25: N = 800 кН; М = 280
кН·м; ![]() = 16;
= 16; ![]() = 0,66.
= 0,66.
Определим значения an и am:
![]()
![]()
По графику б прил. 3 при an = 0,272, am = 0,207 и l = 15 находим as = 0,16.
По графику в прил. 3 при an = 0,272, am = 0,207 и l = 20 находим as = 0,2.
Значение as, соответствующее l = 16, определим линейной интерполяцией:
![]()
Отсюда площадь сечения арматуры равна:
![]() мм2.
мм2.
Принимаем Аs = ![]() = 1362 мм2 (2 Æ 25 + 1 Æ 22).
= 1362 мм2 (2 Æ 25 + 1 Æ 22).
Пример 27. Дано: колонна многоэтажного рамного каркаса с сечением размерами b = 400 мм, h = 500 мм; a = а’ = 40 мм; бетон тяжелый класса В25 (Eb = 2,7 · 104 МПа); арматура симметричная класса А-III (Rs = Rsc = 365 МПа; Еs = 2 · 105 МПа); продольные силы и изгибающие моменты в опорном сечении колонны: от постоянных и длительных нагрузок на перекрытиях Nl = 2200 кН, Ml = 259 кН·м; от ветровых нагрузок Nsh = 0, Msh = 53,4 кН·м; кратковременные нагрузки на перекрытиях отсутствуют; расчетная длина колонны l0 = 6 м.
Требуется определить площадь сечения арматуры.
Расчет. h0 = h – а = 500 – 40 = 460 мм. Поскольку имеется усилие от ветровой нагрузки, проверим условие (1). Для этого вычислим:
![]() кН·м;
кН·м;
![]() кН;
кН;
![]() кН·м;
кН·м;
![]() кН·м.
кН·м.
Так как 0,82 MII = 0,82 · 784,4 = 643 кН·м < MI = 721 кН·м, условие (1) не выполняется и расчет производим дважды: по случаю „а" — на действие длительных и постоянных нагрузок при Rb = 13 МПа (т. е. при gb2 = 0,9) и по случаю „б" — на действие всех нагрузок при Rb = 16 МПа (т. е. при gb2 = 1,1). Расчет производится для опорного сечения.
Расчет по случаю „а". Так как l0/h = 6000/500 = 12 > 4, согласно п. 3.54, следует учитывать прогиб колонны. Однако, согласно п. 3.56, для колонн многоэтажных рам коэффициент hv, вводимый на момент Mv от нагрузок на перекрытиях, принимается равным 1,0, а момент Мh = Msh от ветровых нагрузок в данном расчете не учитывается, поэтому расчетный момент равен М = Мv hv = 259 кН·м.
Расчетная
продольная сила равна N = Nl = 2200 кН,
отсюда ![]() = 118 мм >
= 118 мм >![]() = 16,7 мм. Оставляем e0 = 118 мм.
= 16,7 мм. Оставляем e0 = 118 мм.
По формуле (111) определим е = e0 + (h0 – a’)/2 = 118 + (460 – 40)/2 = 328 мм.
Необходимое армирование определим согласно п. 3.62. Вычислим значения:
![]()
![]()
![]()
Из табл. 18 находим xR = 0,604.
Так как an = 0,92
> xR = 0,604,
значение Аs = ![]() определим по
формуле (113). Для этого по формулам (114) и (109)
вычислим значения as и x:
определим по
формуле (113). Для этого по формулам (114) и (109)
вычислим значения as и x:
![]()
![]()
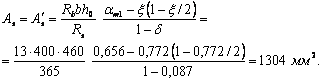
Расчет по случаю „б". Согласно п. 3.54 определим коэффициент h, задаваясь армированием, полученным из расчета по случаю „а", т. е.:
![]()
![]()
[b = 1,0, см. табл. 16];
![]() мм.
мм.
Так как e0/h = ![]() = 0,293 > de,min = 0,5 – 0,01 l0/h – 0,01 Rb = 0,5 –0,01 · 12 – 0,01 · 16 = 0,22, принимаем de = е0/h = 0,293;
= 0,293 > de,min = 0,5 – 0,01 l0/h – 0,01 Rb = 0,5 –0,01 · 12 – 0,01 · 16 = 0,22, принимаем de = е0/h = 0,293;
![]()
По формуле (93) определим Ncr:
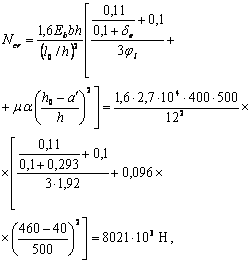
отсюда коэффициент h равен:
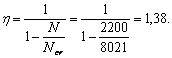
Согласно п. 3.56, коэффициент h = hh = 1,38 умножается на момент от ветровых нагрузок Мsh = M, а коэффициент hv = 1,0, поэтому момент с учетом прогиба колонны равен:
![]() кН·м.
кН·м.
Необходимое армирование определим согласно п. 3.62 аналогично расчету по случаю „а", принимая Rb = 16 МПа:
![]() мм;
мм;
![]()
![]()
Из табл. 18 находим xR = 0,55.
Так как an > xR, значение Аs =
![]() определим по формуле
(113):
определим по формуле
(113):
![]()
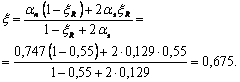
Отсюда

Окончательно
принимаем As = ![]() = 1362 мм2 (2
Æ 25 + 1 Æ 22)
>1304 мм2.
= 1362 мм2 (2
Æ 25 + 1 Æ 22)
>1304 мм2.
Пример 28. Дано: сечение элемента размерами b = 400 мм, h = 600 мм; бетон тяжелый класса В25 (Rb = 16 МПа при gb2 = 1,1; Eb = 2,7 · 104 МПа); арматура класса A-III (Rs = Rsc = 365 МПа; Еs = 2 · 105 МПа) расположена в сечении, как показано на черт. 46; продольные силы и изгибающие моменты: от всех нагрузок N = 500 кН, М = 500 кН·м; от постоянных и длительных нагрузок Nl = 350 кН, Ml = 350 кН·м; расчетная длина l0 = 10 м.
Требуется проверить прочность сечения.
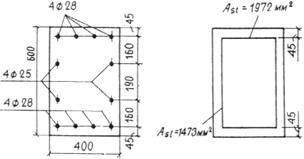
Черт. 46. К примеру расчета 28
Расчет производим согласно п. 3.63. Принимая As1,l = 491 мм2 (Æ 25), hl = 2 и As,tot = 6890 мм2 (8 Æ 28 + 4 Æ 25), находим площади арматуры Asl и Аst:
![]() мм2;
мм2;
![]() мм2.
мм2.
Из черт. 46 имеем
a1 = 45
мм, тогда ![]()
Так как l0/h = 10/0,6 = 16,7 > 10, расчет производим с учетом прогиба элемента согласно п. 3.54, вычисляя значение Ncr по формуле (93).
Для этого определим:
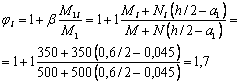
[b = 1,0 (см. табл. 16)];
![]() м.
м.
Так как e0/h = ![]() = 1,67
> de,min = 0,5 – 0,01 l0/h – 0,01 Rb, принимаем de = е0/h = 1,67.
= 1,67
> de,min = 0,5 – 0,01 l0/h – 0,01 Rb, принимаем de = е0/h = 1,67.
Значение ma ![]() определим как
для сечения с арматурой, расположенной по высоте сечения, согласно п. 3.54:
определим как
для сечения с арматурой, расположенной по высоте сечения, согласно п. 3.54:

Отсюда

Коэффициент h равен:
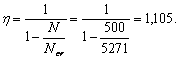
Определим величины:
![]()
![]()
![]()
Из табл. 18 находим w = 0,722 и xR = 0,55.
Так как ![]() 0,24 < xR = 0,55, прочность сечения
проверим из условия (117):
0,24 < xR = 0,55, прочность сечения
проверим из условия (117):
![]()
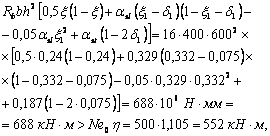
т. е. прочность сечения обеспечена.
Пример 29. Дано: сечение колонны размерами b = 600 мм, h = 1500 мм; бетон тяжелый класса В30 (Rb = 19 МПа при gb2 = 1,1); арматура класса А-III (Rs = 365 МПа) расположена в сечении, как показано на черт. 47; продольные силы и изгибающие моменты, определенные из расчета рамы по деформированной схеме: от всех нагрузок N = 12 000 кН, М = 5000 кН·м; от постоянных и длительных нагрузок Nl = 8500 кН, Мl = 2800 кН·м; расчетная длина колонны в плоскости изгиба l0 = 18м, из плоскости изгиба l0 = 12 м; фактическая длина колонны l = 12 м.
Требуется проверить прочность сечения.
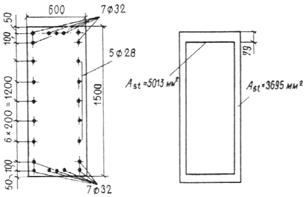
Черт. 47. К примеру расчета 29
Расчет в плоскости изгиба производим согласно п. 3.63.
Принимая As1,l = 615, 8
мм2 (Æ 28), hl = 5 и As,tot = 17 417
мм2 (14 Æ 32 + 10 Æ 28),
находим площади арматуры Аsl и Аst: Аsl = Аs1,l (hl + 1) = 615, 8 (5 + 1)
= 3695 мм2, ![]() мм2.
мм2.
Центр тяжести арматуры, расположенной у растянутой грани (7 Æ 32), отстоит от этой грани на расстоянии
![]() мм,
мм,
тогда
![]()
Определим величины:
![]()
![]()
![]()
Из табл. 18 находим w = 0,698 и xR = 0,523. Так как ![]() 0,584 > xR = 0,523,
прочность сечения проверим из условия (118).
0,584 > xR = 0,523,
прочность сечения проверим из условия (118).
Для этого вычислим:
![]()
![]()
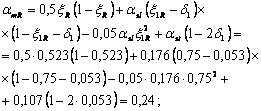
![]()
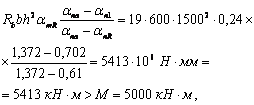
т. е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба. Так как расчетная длина из плоскости изгиба l0 = 12 м и отношение l0/b = 12/0,6 = 20 значительно превышает отношение l0/h = 18/1,5 = 12, соответствующее расчету колонны в плоскости изгиба, согласно п. 3.51, следует рассчитывать колонну из плоскости изгиба, принимая эксцентриситет е0 равным случайному эксцентриситету еa. При этом заменим обозначения h и b соответственно на b и h, т. е. за высоту сечения принимаем его размер из плоскости изгиба h = 600 мм.
Поскольку
случайный эксцентриситет, согласно п. 3.50, равен ![]() и l0 = 12
м £ 20h,
расчет производим согласно п. 3.64.
и l0 = 12
м £ 20h,
расчет производим согласно п. 3.64.
Площадь
сечения промежуточных стержней, расположенных по коротким сторонам, равна As,int =
4826 мм2 (6 Æ 32). Поскольку ![]() = 5800
мм2 > As,int = 4876
мм2 и а = 50 мм < 0,15h = 0,15 · 600 = 90 мм, в
расчете используем табл. 27 (разд. А).
Из табл. 26 и 27 при
= 5800
мм2 > As,int = 4876
мм2 и а = 50 мм < 0,15h = 0,15 · 600 = 90 мм, в
расчете используем табл. 27 (разд. А).
Из табл. 26 и 27 при ![]() и
и ![]() находим jb = 0,674 и jsb = 0,77.
находим jb = 0,674 и jsb = 0,77.
Значение ![]()
По формуле (120) определим коэффициент j:
![]()
Проверим условие (119):
![]()
т. е. прочность сечения из плоскости изгиба обеспечена.
Пример 30. Дано: колонна сечением 400Х400 мм; расчетная длина равна фактической l = l0 = 6 м; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9); продольная арматура класса A-III (Rsc = 365 МПа); центрально-приложенные продольные силы: от постоянных и длительных нагрузок Nl = 1800 кН; от кратковременной нагрузки Nsh = 200 кН.
Требуется определить площадь сечения продольной арматуры.
Расчет, согласно п. 3.50, производим с учетом случайного эксцентриситета ea.
Поскольку h/30 =
400/30 = 13,3 мм >
![]() = 10 мм, случайный эксцентриситет принимаем
равным ea = h/30, тогда расчет можно производить
согласно п. 3.64, принимая N = Nl + Nsh = 1800
+ 200 = 2000
кН.
= 10 мм, случайный эксцентриситет принимаем
равным ea = h/30, тогда расчет можно производить
согласно п. 3.64, принимая N = Nl + Nsh = 1800
+ 200 = 2000
кН.
Из табл. 26 и 27 для тяжелого бетона при Nl/N = 1800/2000 = 0,9, l0/h = 6000/400 = 15, предполагая отсутствие промежуточных стержней при а = а' < 0,15 h, находим jb = 0,8 и jsb = 0,858.
Принимая в первом приближении j = jsb = 0,858, из условия (119) находим
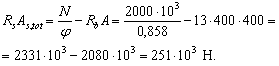
Отсюда ![]()
Поскольку as < 0,5, уточняем значение j, вычисляя его по формуле (120):
![]()
Аналогично определяем
![]()
Полученное значение RsAs,tot существенно превышает принятое в первом приближении, поэтому еще раз уточняем это значение:
![]()
![]()
![]()
Поскольку полученное значение RsAs,tot близко к принятому во втором приближении, суммарную площадь сечения арматуры принимаем равной:
![]() мм2.
мм2.
Окончательно принимаем As,tot = 1018 мм2 (4 Æ 18).
ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
С НЕСИММЕТРИЧНОЙ АРМАТУРОЙ
Пример 31. Дано: сечение элемента размерами b = 400 мм, h = 500 мм; a = a' = 40 мм; бетон тяжелый класса B25 (Rb = 13 МПа при gb2 = 0,9; Eb = 2,7 · 104); арматура класса A-III (Rs = Rsc = 365 МПа); продольная сила N = 800 кН; ее эксцентриситет относительно центра тяжести бетонного сечения е0 = 500 мм; расчетная длина l0 = 4,8 м.
Требуется определить площади сечения арматуры S и S’.
Расчет. h0 = 500 – 40 = 460 мм. Так как 4 < l0/h = 4,8/0,5 = 9,6 < 10, расчет производим с учетом прогиба элемента согласно п. 3.54. При этом, предположив, что m £ 0,025, значение Ncr определим по упрощенной формуле
![]()
Коэффициент h вычислим по формуле (91):

Значение e с учетом прогиба элемента равно:
![]() мм.
мм.
Требуемую площадь сечения арматуры S’ и S определим по формулам (121) и (122):
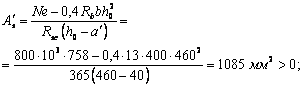

Поскольку ![]() 0,018 < 0,025,
значения Аs
и
0,018 < 0,025,
значения Аs
и ![]() не уточняем.
не уточняем.
Принимаем ![]() =
1232 мм2 (2 Æ 28), Аs = 2627 мм2 (2 Æ 32 + 1 Æ 36).
=
1232 мм2 (2 Æ 28), Аs = 2627 мм2 (2 Æ 32 + 1 Æ 36).
ЭЛЕМЕНТЫ С КОСВЕННЫМ АРМИРОВАНИЕМ
Пример 32. Дано: колонна связевого каркаса с размерами сечения и расположением арматуры по черт. 48; бетон тяжелый класса В40 (Rb = 20 МПа при gb2 = 0,9; Rb,ser = 29 МПа; Eb = 3,25 · 104 МПа); продольная арматура класса A-VI; сетки косвенного армирования из стержней класса A-III, диаметром 10 мм (Rs,xy = 365 МПа), расположенные с шагом s = 130 мм по всей длине колонны; продольная сила при gf > 1,0: от всех нагрузок N = 6600 кН, от постоянных и длительных нагрузок Nl = 4620 кН; то же, при gf = 1,0: N = 5500 кН и Nl = 3850 кН; начальный эксцентриситет продольной силы e0 = ea = 13,3 мм; расчетная длина колонны l0 = 3,6 м.
Требуется проверить прочность колонны.
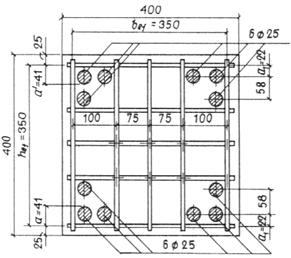
Черт. 48. К примеру расчета 32
Расчет. Проверим прочность сечения, заключенного внутри контура сеток, с учетом косвенного армирования согласно п. 3.57. Расчетные размеры сечения hef = bef = 350 мм. Поскольку l0/hef = 3600/350 = 10,3 < 16, косвенное армирование можно учитывать при расчете, при этом следует учитывать прогиб колонны согласно пп. 3.54 и 3.58, так как l0/hef > 4.
Принимая l0/cef = l0/hef = 10,3 и h = hef = 350 мм, получим

Следовательно,
принимаем de = de,min = 0,297. Поскольку промежуточные стержни
продольной арматуры располагаются в крайних четвертях расстояния между
крайними стержнями, равного h –2a1 = 350 – 2 · 22 = 306 мм [58 мм < ![]() = 76,5 мм (см. черт. 48)], согласно примечанию к п. 3.63 принимаем арматуру S и S’
как сосредоточенную по линиям их центров тяжести. Тогда, учитывая, что все
стержни одинакового диаметра, имеем:
= 76,5 мм (см. черт. 48)], согласно примечанию к п. 3.63 принимаем арматуру S и S’
как сосредоточенную по линиям их центров тяжести. Тогда, учитывая, что все
стержни одинакового диаметра, имеем:
![]() мм;
мм;
![]() мм.
мм.
Коэффициент jl
определим по формуле (94), принимая b = 1,0
(см. табл. 16) и ![]()
![]()
Значение критической силы Ncr определим по формуле (93), принимая
![]() мм2 (6 Æ 25),
мм2 (6 Æ 25),
![]()
и умножая полученное значение на
коэффициент jl = 0,25 + 0,05 ![]() = 0,25 + 0,05 ·
10,3 = 0,764:
= 0,25 + 0,05 ·
10,3 = 0,764:

Коэффициент h равен:
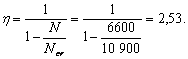
Отсюда, согласно формуле (111),
![]() мм.
мм.
Определим приведенную призменную прочность Rb,red согласно п. 3.57.
Принимая Аsx = Аsy = 78,5 мм2 (Æ 10), nx = ny = 5, lx = ly = 350 мм и Aef = hefbef = 350 · 350 = 122 500 мм2 (см. черт. 48), вычислим коэффициент
![]()
тогда
![]()
![]()
![]() МПа.
МПа.
Поскольку здесь применена высокопрочная арматура класса A-VI, приведенное расчетное сопротивление арматуры сжатию определим согласно п. 3.59:
![]() мм2;
мм2;
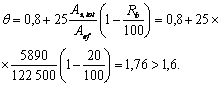
Принимаем q = 1,6.
![]()
Из табл. 25 l1 = 2,04, l2 = 0,77, Rsc = 500 МПа, Rs = 815 МПа,
тогда

Прочность сечения проверим из условия (108), определяя высоту сжатой зоны х = xh0 по формуле (110а).
Для этого по формуле (104) определим значение w. Поскольку 10mxy = 10 · 0,0173 = 0,173 > 0,15, принимаем d2 = 0,15, тогда w = 0,85 – 0,008 Rb + d2 = 0,85 – 0,008 · 20 + 0,15 = 0,84 £ 0,9.
Определим,
согласно пп. 3.61 и 3.65, необходимые коэффициенты an, as, ![]() и yc, приняв Rb = Rb,red = 34,3 МПа; ssc,u = 380 + 1000 d3 = 380 +
1000 · 0,54 = 920
МПа < 1200 МПа и Rsc = Rsc,red = 742 МПа:
и yc, приняв Rb = Rb,red = 34,3 МПа; ssc,u = 380 + 1000 d3 = 380 +
1000 · 0,54 = 920
МПа < 1200 МПа и Rsc = Rsc,red = 742 МПа:
![]()
![]()
![]()
![]()
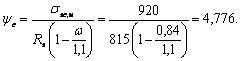
Отсюда
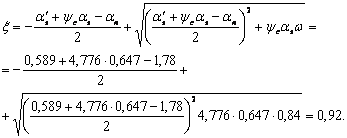
Значение xR с заменой Rs на 0,8Rs равно:
![]()
т . е. использование формулы (110a) оправдано;
![]() мм;
мм;
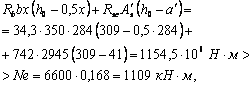
т. е. прочность сечения обеспечена.
Проверим трещиностойкость защитного слоя колонны аналогичным расчетом на действие силы N = 5500 кН (при gf = 1,0), принимая, согласно п. 3.60, Rb = Rb,ser = 29 МПа, Rs = Rs,ser = 980 МПа, Rsc = 400 МПа, ssc,u = 400 МПа, w = 0,85 – 0,006 Rb,ser = 0,85 – 0,006 · 29 = 0,679 и рассматривая полное сечение колонны, т. е. b = h = 400 мм, a = a¢ =41 + 25 = 66 мм, h0 = 400 – 66 = 334 мм.
Критическую
силу Ncr определим по формуле (93), принимая l0/h
= 3600/400 = 9, e0/h = 13,3/400 = 0,033, de,min =
0,5 – 0,01 ![]() – 0,008 Rb,ser = 0,5 – 0,01 · 9 – 0,008 · 29 = 0,178 > e0/h, т. е. de = de,min = 0,178.
– 0,008 Rb,ser = 0,5 – 0,01 · 9 – 0,008 · 29 = 0,178 > e0/h, т. е. de = de,min = 0,178.
При
определении коэффициента jl учитываем продольные
силы N и Nl при gf = 1,0, т.
е. ![]()
тогда jl = 1 + 0,7 = 1,7;
![]()

Коэффициент равен:

![]() мм.
мм.
Произведем расчет аналогично расчету на прочность:
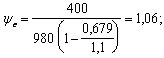
![]()
![]()
![]()
![]()

![]() мм;
мм;
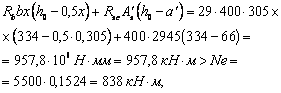
т. е. трещиностойкость защитного слоя обеспечена.
ДВУТАВРОВЫЕ СЕЧЕНИЯ
Пример 33. Дано: размеры сечения и расположение арматуры ¾ по черт. 49; бетон тяжелый класса В30 (Eb = 2,9 · 104 МПа; Rb = 19 МПа при gb2 = 1,1); арматура класса А-III (Rs = Rsc = 365 МПа); площадь ее поперечного сечения As = A¢s = 5630 мм2 (7 Æ 32); продольные силы и изгибающие моменты: от постоянных и длительных нагрузок Nl = 2000 кН, Ml = 2460 кН·м; от всех нагрузок N = 2500 кН, М = 3700 кН·м; расчетная длина элемента: в плоскости изгиба l0 = 16,2 м, из плоскости изгиба l0 = 10,8 м; фактическая длина элемента l = 10,8 м.
Требуется проверить прочность сечения.
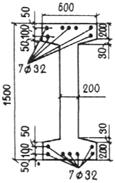
Черт. 49. К примерам расчета 33, 34 и 39
Расчет в плоскости изгиба. Принимаем расчетную толщину полки равной средней высоте свесов h¢f = hf = 200 + 30/2 = 215 мм.
Вычислим площадь и момент инерции бетонного сечения:
![]() мм2;
мм2;
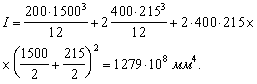
Радиус инерции
сечения ![]() мм.
мм.
Так как l0/i = 16 200/520 = 31,1 < 35 и l0/i > 14, расчет производим с учетом прогиба элемента согласно п. 3.54, принимая значение Ncr равным:

Коэффициент h определим по формуле (91):
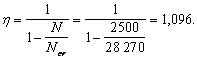
Центр тяжести
площади арматуры As и A¢s отстоит от
ближайшей грани на расстоянии а = а¢
= ![]() мм, откуда h0 = h – a = 1500 – 79 = 1421 мм.
мм, откуда h0 = h – a = 1500 – 79 = 1421 мм.
Значение е с учетом прогиба элемента равно:
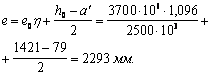
Проверим условие (130):
![]()
т. е. расчет производим как для двутаврового сечения.
Площадь сжатых свесов полки равна:
![]() мм2.
мм2.
Определим высоту сжатой зоны:
![]() мм.
мм.
Из табл. 18 находим xR = 0,523. Так как х = 228 мм < xR h0 = 0,523 · 1421 = 743 мм, прочность сечения проверим из условия (131):
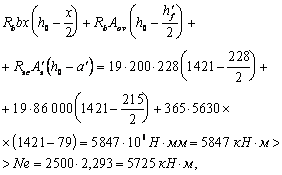
т. е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба. Определим радиус инерции сечения из плоскости изгиба:
![]() мм4;
мм4;
![]() мм.
мм.
Так как гибкость из плоскости изгиба l0/i = 10 800/134 = 80 значительно превышает гибкость в плоскости изгиба l0/i = 31,1, согласно п. 3.51 проверим прочность сечения из плоскости изгиба, принимая эксцентриситет е0 равным случайному эксцентриситету еа. Высота сечения при этом равна h = 600 мм.
Поскольку
случайный эксцентриситет, согласно п. 3.50, еа
= ![]() мм
мм ![]() мм, принимаем еа =
мм, принимаем еа = ![]() что при
что при ![]() позволяет производить
расчет, согласно п. 3.64, как для прямоугольного сечения, не учитывая в „запас” сечение ребра, т. е.
принимая b = 2 · 215 = 430 мм.
позволяет производить
расчет, согласно п. 3.64, как для прямоугольного сечения, не учитывая в „запас” сечение ребра, т. е.
принимая b = 2 · 215 = 430 мм.
Площадь сечения промежуточных стержней, расположенных вдоль обеих полок, равна As,int = 4826 мм2 (6 Æ 32), а площадь сечения всех стержней As,tot = 11 260 мм2 (14 Æ 32). Поскольку As,tot/3 = 11 260/3 = 3750 мм2 < As,int = 4826 мм2, в расчете используем табл. 27 (разд. Б). Из табл. 27 для тяжелого бетона при Nl/N = 2000/2500 = 0,8 и l0/h = 10,8/0,6 = 18 находим jsb = 0,724.
Значение ![]() Следовательно, j = jsb = 0,724.
Следовательно, j = jsb = 0,724.
Проверим условие (119):
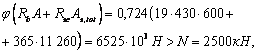
т. е. прочность сечения из плоскости изгиба обеспечена.
Пример 34. Дано: размеры сечения и расположения арматуры ¾ по черт. 49; бетон тяжелый класса В30 (Rb = 19 МПа при gb2 = 1,1; Eb = 2,9 · 104 МПа); арматура симметричная класса A-III (Rs = Rsc = 365 МПа); продольная сила N = 6000 кН; изгибающий момент М = 3100 кН·м; расчетная длина элемента: в плоскости изгиба l0 = 16,2 м, из плоскости изгиба l0 = 10,8 м.
Требуется определить площадь сечения арматуры.
Расчет в плоскости изгиба. Из примера 33 имеем: h¢f = 15 мм; h0 =1421 мм; а¢ = 79 мм; Ncr = 28 270 кН.
По формуле (91) определим коэффициент h:
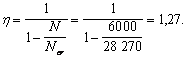
Значение е с учетом прогиба элемента равно:
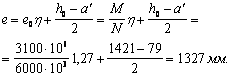
Проверим условие (130):
![]()
т. е. расчет производим как для двутаврового сечения.
Площадь сжатых свесов полки равна:
![]() мм2.
мм2.
Определим значения an, am1, aov, am,ov, d:
![]()
![]()
![]()
![]()
![]()
Из табл. 18 находим xR = 0,523.
Так как x = an – aov =
1,111 – 0,302 = 0,809 > xR = 0,523, площадь арматуры определим по формуле (135).
Для этого по формулам (136) и (132) вычислим значения as и ![]()
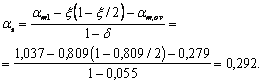
Из табл. 18 находим yс = 3,0 и w = 0,698.
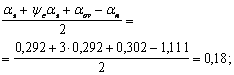

отсюда

Принимаем As = A¢s = 5630 мм2 (7 Æ 32).
Расчет из плоскости изгиба производим аналогично примеру 33.
КОЛЬЦЕВЫЕ СЕЧЕНИЯ
Пример 35. Дано: сечение с внутренним радиусом r1 = 150 мм, наружным ¾ r2 = 250 мм; бетон тяжелый класса В25 (Rb = 16 МПа при gb2 = 1,1); продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь ее сечения As,tot = 1470 мм2 (13 Æ 12); продольная сила от полной нагрузки N = 1200 кН, ее эксцентриситет относительно центра тяжести сечения с учетом прогиба элемента равен е0 = 120 мм.
Требуется проверить прочность сечения.
Расчет. Вычислим площадь кольцевого сечения:
![]() мм2
мм2
Относительная площадь сжатой зоны бетона равна:
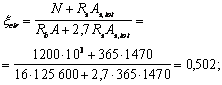
![]() мм.
мм.
Так как 0,15 < xcir = 0,502 < 0,6, прочность сечения проверим из условия (138):
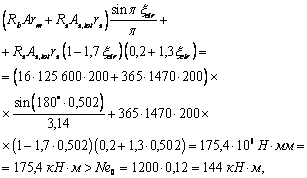
т. е. прочность сечения обеспечена.
КРУГЛЫЕ СЕЧЕНИЯ
Пример 36. Дано: сечение диаметром D = 400 мм; а = 35 мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb2 = 0,9; Eb = 2,7 · 104 МПа); продольная арматура класса A-III (Rs =Rsc = 365 МПа; Es = 2 · 105 МПа); площадь ее сечения As,tot = 3140 мм2 (10 Æ 20); продольные силы и изгибающие моменты: от постоянных и длительных нагрузок Nl = 400 кН·м; от всех нагрузок N = 600 кН, М = 140 кН·м; расчетная длина элемента l0 = 4 м.
Требуется проверить прочность сечения.
Расчет. Вычислим:
площадь
круглого сечения ![]() мм2;
мм2;
радиус инерции
сечения ![]() мм;
мм;
гибкость
элемента ![]()
Следовательно, расчет производим с учетом влияния прогиба элемента согласно п. 3.54, а значение Ncr определим по формуле (92). Для этого вычислим:
![]() мм;
мм;

[здесь b = 1,0 (см. табл. 16)];
![]()
Так как ![]() 0,583 > de,min = 0,5 – 0,01 l0/D – 0,01 Rb, принимаем de = e0/D = 0,583.
0,583 > de,min = 0,5 – 0,01 l0/D – 0,01 Rb, принимаем de = e0/D = 0,583.
Моменты инерции бетонного сечения и всей арматуры соответственно равны:
![]() мм4;
мм4;
![]() мм4;
мм4;
![]()
Тогда

Коэффициент h определим по формуле (91):
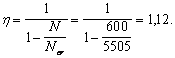
Прочность сечения проверим с помощью графика черт. 41.
По значениям ![]()
![]() 0,702 и
0,702 и ![]() на графике находим am =
0,51.
на графике находим am =
0,51.
Поскольку amRbAr = 0,51 · 13 · 125 600 · 200 = 167 · 106 Н·мм = 167 кН·м > Ne h = 600 · 0,233 · 1,12 = 156,6 кН·м, прочность сечения обеспечена.
Пример 37. По данным примера 36 необходимо подобрать продольную арматуру, пользуясь графиком черт. 41.
Расчет. Из примера 36 i = 100 мм, А = 125 600 мм2, rs = 165 мм. Поскольку l0/i = 4000/100 40 > 35, арматуру подбираем с учетом влияния прогиба элемента, вычисляя значение Ncr по формуле (92).
В первом
приближении принимаем As,tot = 0,01 A
= 1256 мм2, откуда ![]() мм4.
мм4.
Из примера 36 jl = 1,695, de = 0,583, I = 1256 · 106 мм4.
Тогда
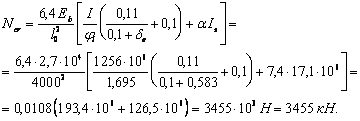
Значение
коэффициента 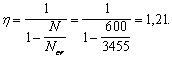
По значениям ![]()
![]() находим as =
0,74, откуда
находим as =
0,74, откуда ![]() мм2.
мм2.
Поскольку полученное армирование существенно превышает принятое в первом приближении (As,tot = 1256 мм2), значение As,tot = 3310 мм2 определено с „запасом”, и его можно несколько уменьшить, уточнив значение Ncr.
Принимаем ![]() мм2 и
производим аналогичный расчет:
мм2 и
производим аналогичный расчет:
![]() мм4;
мм4;
![]() кН;
кН;
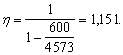
По значениям ![]() an = 0,367 и
an = 0,367 и ![]() на графике черт. 41
находим as = 0,68.
на графике черт. 41
находим as = 0,68.
![]() мм2.
мм2.
Принимаем As,tot = 3142 мм2 (10 Æ 20).
ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ
НА КОСОЕ ВНЕЦЕНТРЕННОЕ СЖАТИЕ
Пример 38. Дано: прямоугольное сечение колонны размерами b = 400 мм, h = 600 мм; бетон тяжелый класса В25 (Rb = 16 МПа при gb2 = 1,1); продольная арматура класса A-III (Rs = Rsc = 365 МПа) расположена в сечении согласно черт. 50; в сечении одновременно действуют продольная сила N = 2600 кН и изгибающие моменты: в плоскости, параллельной размеру h, – Mx = 240 кН·м и в плоскости, параллельной размеру b, – My = 182,5 кН·м; моменты Мх и Мy даны с учетом прогиба колонны.
Требуется проверить прочность сечения.
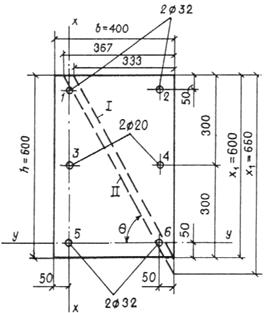
Черт. 50. К примерам расчета 38 и 40
I ¾ граница сжатой зоны в первом приближении; II ¾ окончательная
граница сжатой зоны
Расчет. Прочность проверим согласно п.
3.74. Оси симметрии, параллельные размерам h и b, обозначим соответственно x и y. Определим предельные моменты ![]() и
и ![]() . Для этого вычислим распределенное армирование Asx и Asy. Из черт. 50 As1, x = 0, nx = 0, As0
= 804,3 мм2 (Æ 32), As1, y = 314,2 мм2 (Æ
20),
. Для этого вычислим распределенное армирование Asx и Asy. Из черт. 50 As1, x = 0, nx = 0, As0
= 804,3 мм2 (Æ 32), As1, y = 314,2 мм2 (Æ
20),
![]()
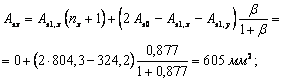
![]() мм2 (4 Æ
32 + 2 Æ
20);
мм2 (4 Æ
32 + 2 Æ
20);
![]() мм2.
мм2.
При
определении, согласно п. 3.63, момента ![]() , действующего в плоскости оси х, принимаем: Asl = Asy = 1318 мм2; Ast = Asx
= 605 мм2; h =
600 мм; b = 400 мм.
, действующего в плоскости оси х, принимаем: Asl = Asy = 1318 мм2; Ast = Asx
= 605 мм2; h =
600 мм; b = 400 мм.
![]()
![]() Н;
Н;
![]()
![]()
![]()
Так как ![]() 0,534 < xR = 0,55, значение
0,534 < xR = 0,55, значение ![]() определим по формуле
(117), вычислив
определим по формуле
(117), вычислив ![]() = 0,74:
= 0,74:

При
определении момента ![]() , действующего в плоскости оси y,
принимаем: Asl = Asx = 605
мм2; Ast = Asy =
1318 мм2; h = 400 мм; b = 600 мм;
, действующего в плоскости оси y,
принимаем: Asl = Asx = 605
мм2; Ast = Asy =
1318 мм2; h = 400 мм; b = 600 мм;
![]()
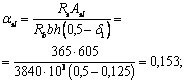
![]()
Так как ![]() 0,583 > xR = 0,55, значение
0,583 > xR = 0,55, значение ![]() определим по формуле
(118), вычислив:
определим по формуле
(118), вычислив:
![]()
![]()
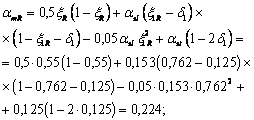
![]()
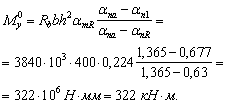
Поскольку ![]() прочность сечения
проверим по графикам черт. 42, а, б, соответствующим as = 0,2 и as = 0,4. На обоих графиках
точка с координатами
прочность сечения
проверим по графикам черт. 42, а, б, соответствующим as = 0,2 и as = 0,4. На обоих графиках
точка с координатами ![]() = 240/464,7 = 0,516 и
= 240/464,7 = 0,516 и ![]() = 182,5/322 = 0,566
лежит внутри области, ограниченной кривой, отвечающей параметру an1
= 0,677, и осями координат.
= 182,5/322 = 0,566
лежит внутри области, ограниченной кривой, отвечающей параметру an1
= 0,677, и осями координат.
Следовательно, прочность сечения обеспечена.
Пример 39. Дано: сечение колонны, характеристики материалов и значение продольной силы от всех нагрузок ¾ из примера 33; в сечении одновременно действуют изгибающие моменты в плоскости, параллельной размеру h, – Mx = 3330 кН·м и в плоскости, параллельной размеру b, – My = 396 кН·м; моменты Мх и Мy даны с учетом прогиба колонны.
Требуется проверить прочность сечения.
Расчет. Прочность проверим согласно п.
3.75. Определим предельный момент ![]() , действующий в плоскости оси симметрии х, проходящей в ребре. Согласно примеру 33, правая часть условия
(131) равна 5847 кН·м,
тогда
, действующий в плоскости оси симметрии х, проходящей в ребре. Согласно примеру 33, правая часть условия
(131) равна 5847 кН·м,
тогда

Предельный
момент ![]() , действующий в плоскости оси симметрии y,
нормальной к ребру, определим как для прямоугольного сечения, составленного их
двух полок, согласно п. 3.63. Тогда, согласно черт. 49, имеем: h = 600 мм;
b = 2 · 215 = 430 мм.
, действующий в плоскости оси симметрии y,
нормальной к ребру, определим как для прямоугольного сечения, составленного их
двух полок, согласно п. 3.63. Тогда, согласно черт. 49, имеем: h = 600 мм;
b = 2 · 215 = 430 мм.
Определим распределенное армирование Asl и Ast:
![]() мм2 (Æ
32); hl = 3;
мм2 (Æ
32); hl = 3;
![]() мм2 (14 Æ
32);
мм2 (14 Æ
32);
Asl = As1, l (nl + 1) = 804,3 (3 + 1) = 3220 мм2;
Ast = As, tot/2 – Asl = 11 260/2 – 3220 = 2410 мм2.
Из табл. 18 находим w = 0,698 и xR = 0,523.
Rbbh = 19 · 430 · 600 = 4902 · 103 H;
d1 = a1/h = 0,083;
![]()
![]()
![]()
![]()
Значение ![]() определим по формуле
(117), вычислив
определим по формуле
(117), вычислив ![]()

Проверим прочность сечения, принимая b = 200 мм, h = 1500 мм.
Поскольку ![]() прочность сечения
проверим по графикам черт. 44, б, в, соответствующим as = 0,6 и
as =
1,0.
прочность сечения
проверим по графикам черт. 44, б, в, соответствующим as = 0,6 и
as =
1,0.
На обоих
графиках точка с координатами ![]() = 3330/4170 = 0,8 и
= 3330/4170 = 0,8 и ![]() = 396/1029 = 0,385 лежит внутри области, ограниченной кривой,
отвечающей параметру an1
= N/(Rbbh)
= 2500 · 103/(19
· 200 · 1500) = 0,44, и осями
координат.
= 396/1029 = 0,385 лежит внутри области, ограниченной кривой,
отвечающей параметру an1
= N/(Rbbh)
= 2500 · 103/(19
· 200 · 1500) = 0,44, и осями
координат.
Следовательно, прочность сечения обеспечена.
Пример 40. Дано: прямоугольное сечение колонны размерами b = 400 мм, h = 600 мм; бетон тяжелый класса В25 (Rb = МПа при gb2 = 1,1); продольная арматура класса A-III (Rs = 365 МПа) по черт. 50; в сечении одновременно действуют продольная сила N = 2600 кН и изгибающие моменты в плоскости, параллельной размеру h, – Мх = 250 кН·м и в плоскости, параллельной размеру b, My = 200 кН·м; изгибающие моменты Мх и My даны с учетом прогиба колонны.
Требуется проверить прочность сечения, пользуясь формулами п. 3.76 для общего случая расчета.
Расчет. Все стержни обозначим номерами, как показано на черт. 50. Через центр тяжести наиболее растянутого стержня 5 проводим ось х параллельно размеру h = 600 мм и ось y параллельно размеру b.
Угол q между осью y и прямой, ограничивающей сжатую зону, принимаем, как при расчете упругого тела на косое внецентренное сжатие, т. е.:
![]()
Задаваясь
значением х1 ¾
размером сжатой зоны по наиболее сжатой стороне сечения h, можно
определить для каждого стержня отношение xi = x/h0i по
формуле ![]() где axi и ayi расстояния от i-го стержня до наиболее
сжатой стороны сечения в направлении осей соответственно х и у.
где axi и ayi расстояния от i-го стержня до наиболее
сжатой стороны сечения в направлении осей соответственно х и у.
По значениям xi определим напряжение ssi, принимая ssc,u = 400 МПа, w = 0,722 (см. табл. 18):

При этом, если ssi > Rs = 365 МПа, что равносильно условию xi < xR = 0,55 (см. табл. 18), принимаем ssi < Rs = 365 МПа.
Если ssi < –Rsc = –365 МПа, принимаем ssi = –365 МПа.
Последнее условие после подстановки в него выражения для ssi приобретет вид
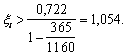
Затем определим сумму усилий во всех стержнях åAsissi.
Задаваясь в первом приближении значением x1 = h = 600 мм, произведем указанные вычисления, результаты которых приводим в следующей таблице:
|
Номер |
Asi, |
ayi, |
axi, |
ayitgq + axi, |
х1 = 600 мм |
х1 = 660 мм |
||||
|
стержня |
мм2 |
мм |
мм |
мм (tgq = 1,8) |
xi |
ssi, МПа |
Asissi, H |
xi |
ssi, МПа |
Asissi, H |
|
1 |
804,3 |
350 |
50 |
680 |
0,882 |
–210 |
–168 900 |
0,971 |
–297 |
–238 877 |
|
2 |
804,3 |
50 |
50 |
140 |
4,29 |
–365 |
–293 570 |
4,714 |
–365 |
–293 570 |
|
3 |
314,2 |
350 |
300 |
930 |
0,645 |
138 |
43 360 |
0,71 |
20 |
6284 |
|
4 |
314,2 |
50 |
300 |
390 |
1,54 |
–365 |
–114 683 |
1,692 |
–365 |
–114 683 |
|
5 |
804,3 |
350 |
550 |
1180 |
0,508 |
365 |
293 570 |
0,56 |
339 |
272 658 |
|
6 |
804,3 |
50 |
550 |
640 |
0,937 |
266 |
213 944 åAsissi = –26 280 H |
1,031 |
–348 |
–279 896 åAsissi = –648 080 H |
Так как ![]() мм < b = 400 мм, форма
сжатой зоны треугольная и площадь ее равна:
мм < b = 400 мм, форма
сжатой зоны треугольная и площадь ее равна:
![]() мм2.
мм2.
Проверим условие (154):
![]()
т. е. площадь сжатой зоны занижена.
Увеличим значение х1 до 660 мм и аналогично определим åAsissi (см. таблицу к настоящему примеру).
При х1 > h и х1/tgq = 660/1,8 = 367 мм < b = 400 мм форма сжатой зоны трапециевидная и площадь ее равна:
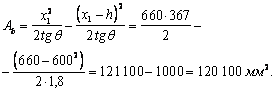
Поскольку RbAb – åAsissi = 16 · 120 100 + 648 080 = 2570 · 103 H = 2570 кН » N = 2600 кН, условие (154) соблюдается.
Определим моменты внутренних сил относительно осей у и х. Для этого определим статические моменты площади сечения сжатой зоны относительно этих осей:


Тогда Mxu = RbSbx – åAsissi (ах5 – аxi) = 16 · 40 036 000 – [–238 877 (550 – 50) – 293 570 (550 – 50) + 6284 (550 – 300) – 114 683 (550 – 300)] = 933,9 · 106 Н · мм = 934 кН · м;

Моменты внешних сил относительно осей у и х равны:
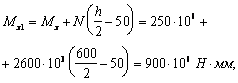
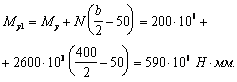
Поскольку Mxu >Mx1, а Myu > My1 прочность сечения обеспечена.
РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ
Пример 41. Дано: колонна многоэтажного каркаса с сечением размерами b = 400 мм, h = 600 мм; а = а¢ = 50 мм; бетон тяжелый класса В25 (Rbt = 0,95 МПа при gb2 = 0,9); хомуты, расположенные по граням колонны, из арматуры класса A-III, диаметром 10 мм (Rsw = 255 МПа; Asw = 157 мм2), шагом s = 400 мм; изгибающие моменты в верхнем и нижнем опорных сечениях равны Msup = 350 кН·м, Minf = 250 кН·м и растягивают соответственно левую и правую грани колонн; продольная сила N = 572 кН; длина колонны (расстояние между опорными сечениями) l = 2,8 м.
Требуется проверить прочность наклонных сечений колонны по поперечной силе.
Расчет. h0 = h – a = 600 – 50 = 550 мм. Расчет производим согласно п. 3.31 с учетом рекомендаций п. 3.53.
Поперечная сила в колонне равна:
![]() кН.
кН.
Поскольку поперечная сила постоянна по длине колонны, длину проекции наклонного сечения принимаем максимально возможной, т. е. равной
![]()
Определим коэффициент jn:
![]()
Поскольку с = сmax, Qb = Qb,min = jb3 (1 + jn)Rbtbh0 = 0,6 (1 + 0,27)0,95 · 400 · 550 = 159,2 · 103 H < Q = 214 кН, т. е. хомуты требуются по расчету.
Значение qsw определим по формуле (55):
![]() Н/мм.
Н/мм.
Проверим условие (57):
![]()
Поскольку условие (57) не выполняется, определим значение Mb по формуле
![]()
откуда
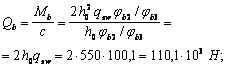
с0 принимаем равным с0 = 2h0 = 2 · 550 = 1100 мм, тогда Qsw = qswc0 = 100,1 · 1100 = 110,1 · 103 Н.
Проверим условие (50):
![]()
т. е. прочность сечений по поперечной силе обеспечена.
Центрально- и внецентренно растянутые элементы
ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
3.77 (3.26). При расчете сечений центрально-растянутых железобетонных элементов должно соблюдаться условие
![]() (156)
(156)
где As,tot ¾ площадь сечения всей продольной арматуры.
ВНЕЦЕНТРЕННО РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ,
НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА,
ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ ОСИ СИММЕТРИИ
3.78 (3.27). Расчет прямоугольных сечений внецентренно растянутых элементов с арматурой, сосредоточенной у наиболее растянутой и у сжатой (наименее растянутой) граней, должен производиться в зависимости от положения продольной силы N:
а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S¢ (черт. 51, а), т. е. при е¢ £ h0 – a¢, ¾ из условий:
![]() (157)
(157)
![]() (158)
(158)
б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S¢ (черт. 51, б), т. е. при е¢ £ h0 – a¢, ¾ из условия
![]() (159)
(159)
при этом высота сжатой зоны х определяется по формуле
![]() (160)
(160)
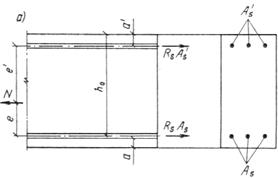
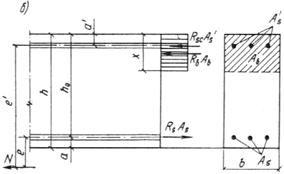
Черт. 51. Схема усилий и эпюра напряжений в сечении, нормальном
к продольной оси внецентренно растянутого железобетонного элемента,
при расчете его по прочности
а ¾ продольная сила N приложена между равнодействующими усилий
в арматуре S и S¢; б ¾ то же, за пределами расстояния между равнодействующими усилий в арматуре S и S¢
Если полученное из расчета по формуле (160) значение х > xRh0, в условие (159) подставляется х = xRh0, где xR определяется по табл. 18 и 19.
Если х < 0, прочность сечения проверяется из условия (157).
При симметричном армировании прочность независимо от значения е¢ проверяется из условия (157).
Примечание.
Если при e¢ > h0 – a¢ высота
сжатой зоны, определенная без учета сжатой арматуры ![]() , меньше 2а¢, расчетную несущую способность можно несколько увеличить, произведя
расчет по формулам (159) и (160) без учета сжатой арматуры.
, меньше 2а¢, расчетную несущую способность можно несколько увеличить, произведя
расчет по формулам (159) и (160) без учета сжатой арматуры.
3.79. Требуемое количество продольной арматуры определяется следующим образом:
а) при e¢ £ h0 – a¢ определяется площадь сечения арматуры S и S¢ соответственно по формулам:
![]() (161)
(161)
![]() (162)
(162)
б) при e¢ > h0 – a¢ определяется площадь сечения растянутой арматуры As по формуле
![]() (163)
(163)
где x принимается по табл. 20 в зависимости от значения
![]() (164)
(164)
При этом
должно удовлетворяться условие am £ aR (см. табл. 18 и 19). В противном
случае следует увеличить сечение сжатой арматуры ![]() , повысить класс бетона или увеличить размеры сечения.
, повысить класс бетона или увеличить размеры сечения.
Если am < 0, площадь сечения растянутой арматуры As определяется по формуле (161).
Площадь симметричной арматуры независимо от значения е¢ подбирается по формуле (161).
Примечание.
При е¢ > h0 – a¢ необходимое
количество арматуры, определенное по формуле (161), можно несколько снизить,
если значение x, определенное по табл. 20 без учета сжатой арматуры, т. е. по значению
![]() окажется меньше 2а¢/h0. В этом случае площадь сечения растянутой арматуры As определяется по формуле
окажется меньше 2а¢/h0. В этом случае площадь сечения растянутой арматуры As определяется по формуле
![]() (165)
(165)
где z определяется по табл. 20 в зависимости от
значения ![]()
ОБЩИЙ СЛУЧАЙ РАСЧЕТА НОРМАЛЬНЫХ СЕЧЕНИЙ
ВНЕЦЕНТРЕННО РАСТЯНУТОГО ЭЛЕМЕНТА
(ПРИ ЛЮБЫХ СЕЧЕНИЯХ, ВНЕШНИХ УСИЛИЯХ
И ЛЮБОМ АРМИРОВАНИИ)
3.80. Расчет сечений внецентренно растянутого элемента в общем случае (см. черт. 45) должен производиться из условия
![]() (166)
(166)
где ![]() ¾
расстояние от продольной силы N до
оси, параллельной прямой, ограничивающей сжатую зону, и проходящей через точку
сжатой зоны, наиболее удаленную от указанной прямой;
¾
расстояние от продольной силы N до
оси, параллельной прямой, ограничивающей сжатую зону, и проходящей через точку
сжатой зоны, наиболее удаленную от указанной прямой;
Sb ¾ статический момент площади сжатой зоны бетона относительно указанной оси;
Ssi ¾ статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;
ssi ¾ напряжение в i-м стержне продольной арматуры.
Высота сжатой зоны х и напряжения ssi определяются из совместного решения уравнений (154) и (155) с заменой перед N знака „минус” знаком „плюс”.
При косом внецентренном растяжении для определения положения границы сжатой зоны кроме использования формул (154) и (155) требуется соблюдение дополнительного условия, чтобы точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре лежали на одной прямой (см. черт. 45).
РАСЧЕТ СЕЧЕНИЙ,
НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.81. Расчет наклонных сечений внецентренно растянутых элементов на действие поперечной силы производится как для изгибаемых элементов согласно пп. 3.28¾3.41. При этом значение Mb в п. 3.31 определяется по формуле
![]() (167)
(167)
где ![]() но не более 0,8;
но не более 0,8;
значение Qb,min принимается равным jb3 (1 + jf – jn)Rbtbh0. Кроме того, во всех формулах пп. 3.29, 3.40 и 3.41 коэффициент jb4 заменяется на jb4 (1 – jn).
Расчет наклонных сечений внецентренно растянутых элементов на действие изгибающего момента производится как для изгибаемых элементов согласно пп. 3.42¾3.45. При этом высота сжатой зоны в наклонном сечении определяется с учетом растягивающей силы N по формуле (160) или согласно п. 3.80.
В случае выполнения условия e¢ < h0 – a¢ расчетный момент в наклонном сечении допускается определять как момент всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно оси, проходлящей через центр тяжести арматуры S¢.
ПРИМЕРЫ РАСЧЕТА
Пример 42. Дано: растянутая ветвь двухветвевой колонны с поперечным сечением размерами b = 500 мм, h = 200 мм; а = а¢ = 40 мм; продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь ее сечения As = A¢s = 982 мм2 (2 Æ 25); бетон тяжелый класса В25 (Rb = 16 МПа при gb2 = 1,1); продольная сила N = 44 кН; максимальный изгибающий момент М = 43 кН · м.
Требуется проверить прочность нормального сечения.
Расчет. h0 = 200 – 40 = 160 мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм.
мм.
Поскольку арматура симметричная, прочность проверим из условия (157):
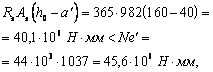
т. е. условие (157) не удовлетворяется. Так как е¢ = 1037 мм > h0 – a¢ = 120 мм, а высота сжатой зоны х, определенная по формуле (160) без учета сжатой арматуры:
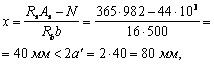
согласно примечанию к п. 3.78 проверим прочность из условия (159), принимая х = 40 мм и A¢s = 0:
![]()
т. е. прочность нормального сечения обеспечена.
Пример 43. Дано: прямоугольное сечение размерами b = 1000 мм, h = 200 мм; а = а¢ = 35 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа при gb2 = 0,9); продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь сечения арматуры S¢ A¢s = 1005 мм2; растягивающая сила N = 160 кН; изгибающий момент М = 116 кН·м.
Требуется определить площадь сечения арматуры S.
Расчет. h0 = 200 – 35 = 165 мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм.
мм.
Так как е¢ = 790 мм h0 – а¢ = 165 – 35 = 130 мм, определим необходимую площадь сечения растянутой арматуры согласно п. 3.79б.
Вычислим значение
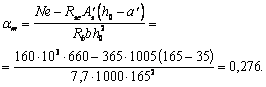
Так как 0 < am < aR = 0,44 (см. табл. 18), значение As определим по формуле (163). Для этого по табл. 20 при am = 0б276 находим x = 0,33.

Принимаем As = 3079 мм2 (5 Æ 28).
Пример 44. Дано: прямоугольное сечение размерами b = 1000 мм, h = 200 мм; а = а¢ = 40 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа при gb2 = 0,9); продольная арматура класса A-III (Rs = Rsc = 365 МПа); растягивающая сила N = 532 кН; изгибающий момент М = 74 кН·м.
Требуется определить площадь сечения симметричной продольной арматуры.
Расчет. h0 = h – a = 200 – 40 = 160 мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм.
мм.
Поскольку арматура симметричная, площадь сечения арматуры определим по формуле (161):
![]() мм2.
мм2.
Так как е¢ = 199 мм > h0 – а¢ = 120 мм, согласно примечанию к п. 3.79 значение As можно снизить.
Определим значение x без учета сжатой арматуры. Для этого вычислим значение am:
![]()
Из табл. 20
при am = 0,213 находим x = 0,24 и z =
0,88. Так как ![]() определим значение As по формуле (165):
определим значение As по формуле (165):
![]() мм2.
мм2.
Принимаем As = A¢s = 2281 мм2 (6 Æ 22).
Пример 45. Дано: растянутая ветвь двухветвевой колонны с сечением размерами b = 500 мм, h = 200 мм; а = а¢ = 40 мм; бетон тяжелый класса В25 (Rbt = 1,15 МПа при gb2 = 1,1); хомуты, расположенные по граням ветви, из арматуры класса A-III (Rsw = 285 МПа); продольная растягивающая сила N = 44 кН; поперечная сила Q = 143 кН; расстояние между перемычками двухветвевой колонны l = 600 мм.
Требуется определить диаметр и шаг хомутов.
Расчет. h0 = h – а = 200 – 40 = 160 мм. Расчет производим согласно п. 3.33а с учетом рекомендаций п. 3.81.
Значение Mb определим по формуле (167), приняв jb2
= 2 (см.
табл. 21), jf = 0 и
![]() 0,096 <
0,8:
0,096 <
0,8:
![]() Н·мм.
Н·мм.
Поскольку в пределах между перемычками поперечная сила постоянна, длину проекции наклонного сечения принимаем максимально возможной, т. е.
![]() мм < l
= 160 мм.
мм < l
= 160 мм.
Тогда
![]()
Так как 2h0 = 2 · 160 = 320 мм < с = 533 мм, принимаем с0 = 2h0 = 320 мм.
Определим коэффициент æ :
æ
![]()
Поскольку ![]() 1,667 < æ
= 1,866 <
1,667 < æ
= 1,866 < ![]() 3,33, интенсивность хомутов определим по формуле (63):
3,33, интенсивность хомутов определим по формуле (63):
![]() кН/м.
кН/м.
Максимально допустимый шаг хомутов, согласно п. 3.30, равен:
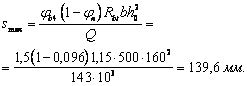
Кроме того, шаг хомутов, согласно п. 5.58, не должен превышать 2h = 2 · 200 = 400 мм.
Принимаем шаг хомутов s = 100 мм < smax, тогда
![]() мм2.
мм2.
Принимаем два хомута диаметром по 10 мм (Asw = 157 мм2).
Элементы, работающие на кручение с изгибом
(расчет пространственных сечений)
ЭЛЕМЕНТЫ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
3.82 (3.37). При расчете элементов на кручение с изгибом должно соблюдаться условие
![]() (168)
(168)
где b, h ¾ соответственно меньший и больший размеры граней элемента.
При этом значение Rb для бетона класса выше В30 принимается как для бетона класса В30.
3.83. Пространственные сечения рассчитываются на совместное действие крутящих и изгибающих моментов, располагая сжатую зону у грани элемента, перпендикулярной плоскости действия изгибающего момента (1-я схема, черт. 52).
Кроме того, пространственные сечения рассчитываются на совместное действие крутящих моментов и поперечных сил, расоплагая сжатую зону у грани элемента, параллельно плоскости действия изгибающего момента (2-я схема, черт. 53).
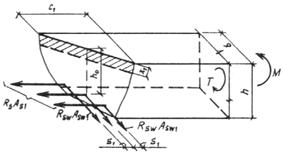
Черт. 52. Схема усилий в пространственном сечении
1-й схемы
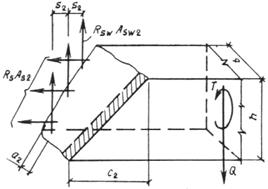
Черт. 53. Схема усилий в пространственном сечении
2-й схемы
3.84. Расчет пространственного сечения по 1-й схеме производится из условия
![]() (169)
(169)
при этом значение RsAs1 принимается не более ![]() а значение qsw1 ¾
не более
а значение qsw1 ¾
не более ![]()
В условии (169):
с1 ¾ длина проекции на
продольную ось элемента линии, ограничивающей сжатую зону пространственного
сечения; невыгоднейшее значение с1
в общем случае определяется последовательными приближениями и принимается не
более 2h + b и не более ![]() при этом
пространственное сечение не должно выходить за пределы элемента и его участка с
однозначными и ненулевыми значениями Т;
при этом
пространственное сечение не должно выходить за пределы элемента и его участка с
однозначными и ненулевыми значениями Т;
As1 ¾ площадь сечения всех продольных стержней, расположенных у растянутой от изгиба грани шириной b;
qsw1 ¾ усилие в поперечных стержнях, расположенных у растянутой от изгиба грани шириной b на единицу длины элемента, равное:
![]() (170)
(170)
где Asw1 ¾ площадь сечения одного поперечного стержня;
s1 ¾ расстояние между поперечными стержнями;
![]() (171)
(171)
Моменты крутящий Т и изгибающий М принимаются в поперечном сечении, проходящем через середину пространственного сечения (черт. 54, а).
Высота сжатой зоны х1 определяется по формуле
![]() (172)
(172)
где ![]() ¾
площадь сечения всех сжатых стержней, расположенных у грани шириной b.
¾
площадь сечения всех сжатых стержней, расположенных у грани шириной b.
Если х1 < 2а¢, в условии (169) принимается х1 = 2а¢. Если х1 > xRh0 (где xR ¾ см. п. 3.14),должна быть проверена прочность нормального сечения согласно п. 3.15.
Условие (169) также должно выполняться, если в качестве значений As1 и Asw1 принимать площади сечения продольной и поперечной арматуры, расположенной в сжатой от изгиба зоне; в этом случае значение М подставляется со знаком „минус”.
Примечание. Ограничение, вводимое на значение RsAs1 при использовании условия (169), допускается учитывать и при использовании формулы (172), что может привести к некоторому увеличению расчетной несущей способности.
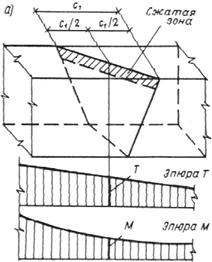
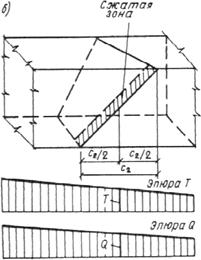
Черт. 54. Определение изгибающего и крутящего моментов
поперечной силы, действующих в пространственном
сечении
а ¾ 1-й схемы; б ¾ 2-й схемы
3.85. Прочность по продольной арматуре, расположенной у растянутой от изгиба грани (1-я схема), рекомендуется проверять:
а) для неразрезных балок и консолей, располагая пространственное сечение у опоры, а также для любых элементов, нагруженных сосредоточенными силами и крутящими моментами, располагая пространственные сечения у мест приложения этих сил и моментов со стороны участка с большими крутящими моментами (черт. 55), ¾ из условия
![]() (173)
(173)
где Mmax ¾ наибольший изгибающий момент в начале пространственного сечения;
T, Q ¾ соответственно крутящий момент и поперечная сила в сечении с наибольшим изгибающим моментом.
При этом qsw1 b(h0 – 0,5x1) принимается не более ![]()
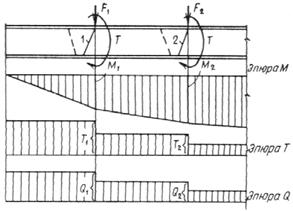
Черт. 55. Расположение расчетных пространственных сечений
1-й схемы в балке, нагруженной сосредоточенными
силами
1, 2 ¾ расчетные пространственные сечения; M1, T1, Q1 ¾
расчетные усилия для пространственного сечения 1;
М2, Т2, Q2 ¾ то же, для пространственного сечения 2
б) для элементов, нагруженных только равномерно распределенной нагрузкой q, если в пролетном сечении с наибольшим изгибающим моментом Mmax имеет место крутящий момент Т0, ¾ из условия
 (174)
(174)
где t ¾ равномерно распределенный крутящий момент на единицу длины элемента.
Прочность по продольной арматуре, расположенной у сжатой от изгиба грани, рекомендуется проверять для свободно опертых балок из условия (173), принимая усилия Т и Q в опорном сечении при Mmax = 0.
Если на рассматриваемых участках выполняется условие
![]() (175)
(175)
продольную арматуру можно проверить только из условия чистого изгиба (см. п. 3.15).
Прочность по поперечной арматуре, расположенной у любой грани шириной b, рекомендуется проверять из условия
![]() (176)
(176)
Примечание. Подобранную из условия (173) продольную арматуру можно несколько уменьшить, если невыгоднейшее пространственное сечение длиной проекции с1, равной:
![]() (177)
(177)
выходит за пределы длины элемента или его участка с однозначными и ненулевыми значениями Т. В этом случае расчет производится общим методом согласно п. 3.84 при соответственно уменьшенной длине проекции с1.
3.86. Расчет пространственного сечения по 2-й схеме (см. черт. 53) производится из условия
![]() (178)
(178)
при этом значение RsAs2 принимается не более 2qsw2h, а значение qsw2 ¾ не более ![]()
В условии (178):
As2 ¾ площадь сечения всех растянутых продольных стержней, расположенных у грани шириной h, параллельной плоскости изгиба;
с2 ¾ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения; невыгоднейшее значение с2 определяется по формуле
![]() (179)
(179)
и принимается не более ![]() и не более 2b + h,
при этом пространственное сечение не должно выходить за пределы элемента и его
участка с однозначными и ненулевыми значениями Т;
и не более 2b + h,
при этом пространственное сечение не должно выходить за пределы элемента и его
участка с однозначными и ненулевыми значениями Т;
![]() (180)
(180)
где Asw2 ¾ площадь сечения одного поперечного стержня, расположенного у грани шириной h;
s2 ¾ расстояние между поперечными стержнями, расположенными у грани шириной h;
![]() (181)
(181)
а2 ¾ расстояние от грани шириной h до оси продольных стержней, расположенных у этой грани.
Крутящийся момент Т и поперечная сила Q принимаются в поперечном сечении, проходящем через середину пространственного сечения (см. черт. 54, б).
В случае,
когда удовлетворяется условие (175), расчет пространственного сечения по 2-й
схеме не производится. Вместо него производится расчет наклонных сечений
согласно пп. 3.31¾3.38
без учета отогнутых стержней. При этом в соответствующих формулах к поперечной
силе Q добавляется величина ![]() (где Т ¾ крутящийся момент
в том же поперечном сечении, что и Q), а величина q1 умножается на коэффициент
(где Т ¾ крутящийся момент
в том же поперечном сечении, что и Q), а величина q1 умножается на коэффициент ![]() (где eq ¾ эксцентриситет
поперечной равномерно распределенной нагрузки q,
вызывающий кручение элемента). В случае, если Т < 0,25Qb, при расчете наклонных сечений
можно учитывать наличие отогнутых стержней.
(где eq ¾ эксцентриситет
поперечной равномерно распределенной нагрузки q,
вызывающий кручение элемента). В случае, если Т < 0,25Qb, при расчете наклонных сечений
можно учитывать наличие отогнутых стержней.
3.87. Необходимую из расчета
пространственного сечения по 2-й схеме интенсивность хомутов ![]() допускается определять
по формулам:
допускается определять
по формулам:
при ![]()
![]() (182)
(182)
при 1,75 ³ jt > 1
![]() (183)
(183)
где T, Q ¾ максимальные значения соответственно крутящего момента и поперечной силы на рассматриваемом участке.
При jt > 1б75 следует увеличить площадь сечения арматуры As2 или размер сечения b так, чтобы было выполнено условие jt £ 1,75.
Если поперечная нагрузка приложена в пределах высоты сечения и действует в сторону растянутой зоны, интенсивность вертикальных хомутов должна быть увеличена по сравнению с вычисленной по формулам (182) и (183) в соответствии с расчетом на отрыв согласно п. 3.97.
ЭЛЕМЕНТЫ ТАВРОВОГО, ДВУТАВРОВОГО
И ДРУГИХ СЕЧЕНИЙ,
ИМЕЮЩИХ ВХОДЯЩИЕ УГЛЫ
3.88. Поперечное сечение элемента следует разбивать на ряд прямоугольников (черт. 56), при этом, если высота свесов полок или ширина ребра переменны, принимаются их средние значения.
Черт. 56. Разделение на прямоугольники сечений,
имеющих входящие углы, при расчете на кручение с изгибом
Размеры поперечного сечения должны удовлетворять условию
![]() (184)
(184)
где hi, bi ¾ соответственно больший и меньший размеры каждого из составляющих сечение прямоугольников.
Кроме того, необходимо соблюдать требование п. 3.30.
Если в пределах высоты сечения имеются полки (выступы), нижние или верхние грани которых не являются продолжение соответствующих граней элемента, расчет пространственных сечений ведется без учета этих полок как для элемента прямоугольного сечения согласно пп. 3.83¾3.87.
3.89. Расчет пространственного сечения на совместное действие крутящего и изгибающего моментов (1-я схема, черт. 57) производится из условия
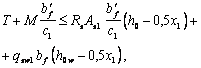 (185)
(185)
при этом значение RsAs1 принимается не более ![]()
В условии (185):
b¢f, bf ¾ ширина соответственно сжатой грани и растянутой грани, нормальной к плоскости изгиба;
с1 ¾ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения; значение с1 принимается соответствующим значению угла наклона пространственной трещины к оси элемента 45° на всех гранях элемента и определяется (без учета х1) по формуле
![]()
при этом длина с1 не должна выходить за пределы элемента и его участка с однозначными и ненулевыми значениями Т;
As1 ¾ площадь сечения всех продольных стержней, расположенных в растянутой от изгиба зоне;
х1 ¾ высота сжатой зоны, определяемая как для плоского поперечного сечения изгибаемого элемента (см. п. 3.20);
![]() (186)
(186)
Asw1, s1 ¾ площадь поперечных стержней, расположенных в одной плоскости в растянутой от изгиба зоне, и шаг этих стержней;
h0w ¾ расстояние от сжатой грани до равнодействующей усилий в поперечных стержнях растянутой зоны.
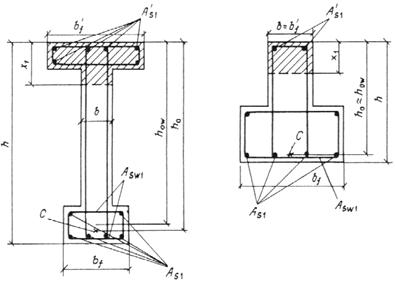
Черт. 57. Схемы расположения сжатой зоны в пространственном
сечении 1-й схемы железобетонного элемента двутаврового
и таврового сечений, работающего на кручение с изгибом
С ¾ центр тяжести продольной растянутой арматуры
Моменты крутящий Т и изгибающий М в условии (185) принимаются в поперечном сечении, проходящем через середину пространственного сечения.
В случае изменения шага поперечных стержней s1 в пределах длины с1 учитывается средний шаг на участке длиной bf, расположенном симметрично относительно поперечного сечения, проходящего через середину пространственного сечения.
Кроме того, следует проверить прочность нормального сечения согласно п. 3.20.
Примечание. Ограничение, вводимое на значение RsAs1 при использовании условия (185), допускается учитывать и при вычислении высоты сжатой зоны х1, что приведет к некоторому увеличению расчетной несущей способности.
3.90. Расчет пространственного сечения на совместное действие крутящего момента и поперечной силы (2-я схема, черт. 58) производится из условия
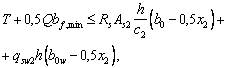 (187)
(187)
при этом значение RsAs2 принимается не более 2qsw2h.
В условии (187):
bf,min ¾ меньшая ширина полки элемента или при одной полке ширина ребра;
As2 ¾ площадь всех продольных стержней, расположенных в растянутой зоне при данной схеме;
с2 ¾ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения, определяемая по формуле
![]()
где bov ¾ ширина свеса полки, расположенного в растянутой зоне, при этом длина с2 не должна выходить за пределы элемента или его участка с однозначными и ненулевыми значениями Т;
х2 ¾ высота сжатой зоны, определяемая как для плоского поперечного сечения изгибаемого элемента при данной схеме расположения сжатой зоны, при этом не учитывается сжатый свес полки, выступающий за грань полки меньшей ширины или за грань ребра при одной полке;
![]() (188)
(188)
Asw2, s2 ¾ соответственно площадь сечения одного поперечного стержня, расположенного в растянутой зоне при данной схеме на всю высоту h, и его шаг;
b0, b0w ¾ расстояния от боковой сжатой грани полки (или ребра) шириной bf,min до равнодействующей усилий соответственно в продольных стержнях площадью As2 и в поперечных стержнях площадью Asw2.
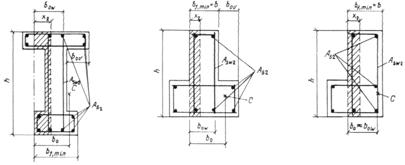
Черт. 58. Схемы расположения сжатой зоны в пространственном сечении 2-й схемы железобетонного элемента двутаврового, таврового
и Г-образного сечений, работающего на кручение с изгибом
С ¾ центр тяжести продольной растянутой арматуры
Крутящий момент Т и поперечная сила Q в условии (187) принимаются в поперечном сечении, проходящем через середину пространственного сечения.
В случае изменения шага поперечных стержней s2 в пределах длины с2 учитывается средний шаг на участке длиной h, расположенном симметрично относительно поперечного сечения, проходящего через середину пространственного сечения.
Кроме того, следует проверить прочность наклонного сечения согласно п. 3.31.
ЭЛЕМЕНТЫ КОЛЬЦЕВОГО СЕЧЕНИЯ
С ПРОДОЛЬНОЙ АРМАТУРОЙ,
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ОКРУЖНОСТИ
3.91. Размеры поперечного кольцевого сечения элемента должны удовлетворять условию
![]() (189)
(189)
где r1, r2 ¾ соответственно внутренний и наружный радиусы кольцевого сечения.
Расчет пространственного сечения (черт. 59) производится из условия
![]() (190)
(190)
где b, c ¾ длина проекции линии, ограничивающей сжатую зону, соответственно на поперечное сечение элемента и на его продольную ось (см. черт. 59). Значение b принимается равным
![]() (191)
(191)
значение с определяется согласно п. 3.91;
![]() - относительная
площадь сжатой зоны бетона определяемая по формуле (137), или при
- относительная
площадь сжатой зоны бетона определяемая по формуле (137), или при ![]() < 0,15 - по формуле (140) при N = 0;
< 0,15 - по формуле (140) при N = 0;
Мu - предельный изгибающий момент при чистом изгибе, принимаемый равным правой части условий (138) или (139);
![]() ; (192)
; (192)
Аsr,s - соответственно площадь сечения стержня спиральной (кольцевой)арматуры и шаг навивки спирали (шаг колец);
![]() - коэффициент,
определяемый по формуле
- коэффициент,
определяемый по формуле
 (193)
(193)
или по черт. 60.
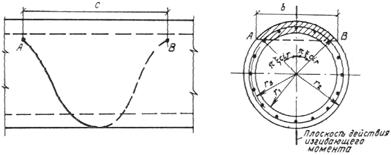
Черт. 59 Пространственное сечение железобетонного элемента кольцевого поперечного сечения, работающего на кручение с изгибом
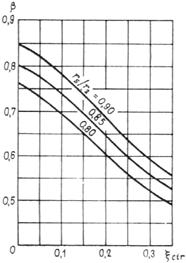
Черт. 60. График для определения коэффициента ![]() при расчете элементов
кольцевого поперечного сечения на кручение с изгибом
при расчете элементов
кольцевого поперечного сечения на кручение с изгибом
Моменты крутящий Т и изгибающий М в условии (190) принимаются в поперечном сечении, проходящем через середину пространственного сечения.
Кроме того,
должно быть проверено условие (190) как при чистом кручении с умножением
величины Мu
на отношение ![]() , где As, tot - площадь сечения всей продольной арматуры.
, где As, tot - площадь сечения всей продольной арматуры.
Значение qsr
в условии (190) принимается не более 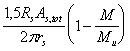 .
.
3.92. Условие (190) проверяется для
пространственных сечений, в которых длина проекции с не выходит за пределы участка с однозначными и ненулевыми
значениями Т и не превышает ![]() .
.
Для элементов с постоянным сечением по длине рекомендуется проверять пространственные сечения, начинающиеся от нормального сечения с наибольшим значением Т, а при постоянных значениях Т - от сечения с наибольшим значением М=Ммах. В последнем случае невыгоднейшее значение с равно:
![]() .
.
Для элементов с переменным сечением по длине рекомендуется проверять несколько пространственных сечений, расположенных в разных местах по длине, и при значениях с, равных:
![]() ,
,
при этом длина проекции с не должна выходить за пределы длины элемента. Размеры поперечного сечения принимаются соответствующими середине пространственного сечения.
ПРИМЕРЫ РАСЧЕТА
Пример 46. Дано: ригель перекрытия торцевой рамы многоэтажного промышленного здания, нагруженный равномерно распределенной нагрузкой q=154,4 кН/м и равномерно распределенными крутящими моментами t=34,28 кН·м/м; поперечное сечение ригеля у опоры - по черт. 61, а; эпюра крутящих моментов от вертикальных постоянных и длительных нагрузок - по черт. 61, б; эпюры изгибающих моментов и поперечных сил от невыгоднейшей для опорного сечения комбинации вертикальных нагрузок и ветровой нагрузки - по черт. 61, в, г; эпюра изгибающих моментов от невыгоднейшей для пролетного сечения комбинации вертикальных нагрузок - по черт. 61, д; бетон тяжелый класса В25; продольная и поперечная арматура класса А-III (Rs=Rsc=365 МПа; Rsw=290 МПа).
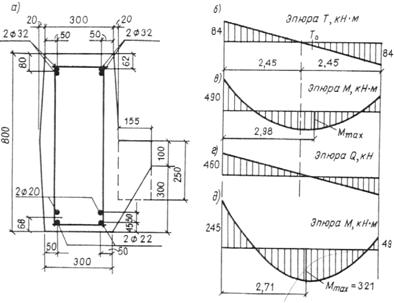
Черт. 61. К примеру расчета 46
Требуется подобрать вертикальные и горизонтальные поперечные стержни и проверить прочность ригеля на совместное действие кручения и изгиба.
Расчет. Поскольку сечение имеет входящие
углы, проверим условие (184), разбив сечение на два прямоугольника размерами
800х320 и 155х250 мм и приняв Rb = 13 МПа (т.е. при ![]() = 0,9);
= 0,9);
![]()
![]() Н·мм > Т = 84 кН·м,
Н·мм > Т = 84 кН·м,
т.е. условие (184) удовлетворяется.
Расчет пространственных сечений производим как для прямоугольного сечения размерами b = 300 мм и h = 800 мм, так как нижняя грань ригеля и выступающая полка образуют угол.
Так как для опорного сечения 0,5Qb=0,5·460·0,3=69 кН·м < Т=84 кН·м, согласно пп. 3.85 и 3.86, расчет приопорного участка по 1-й и 2-й схемам необходим.
Необходимую из расчета по 2-й схеме интенсивность вертикальных стержней определяем согласно п. 3.87.
Предварительно
вычислим коэффициенты ![]() и
и ![]() :
:
![]() ;
;
![]()
![]()
где Аs2 = 1609 + 314 + 380 = 2304 мм2 (2Æ32 + Æ20 + Æ22).
Поскольку ![]() <
1, интенсивность хомутов определим по формуле (182):
<
1, интенсивность хомутов определим по формуле (182):
![]() мм.
мм.
Принимая шаг вертикальных хомутов s2 = 100 мм, находим площадь сечения одного хомута:
Asw2 = 1,54 · 100 = 154 мм2.
Принимаем хомуты диаметром 14 мм (Asw2 = 154 мм2).
Проверим прочность по продольной арматуре, установленной у верхней растянутой грани приопорного участка ригеля согласно п. 3.85а (1-я схема).
Из черт. 61, а находим As1 = 3217 мм2 (4Æ32)
и ![]() = 1388 мм2
(2Æ20
+ 2Æ22),
а' = 68 мм.
= 1388 мм2
(2Æ20
+ 2Æ22),
а' = 68 мм.
По формуле
(172) определим высоту сжатой зоны х1,
принимая Rb = 16 МПа (т.е. при ![]() = 1,1, поскольку учитывается ветровая нагрузка):
= 1,1, поскольку учитывается ветровая нагрузка):
![]() мм >
2а/ = 2 ·
68 =
мм >
2а/ = 2 ·
68 =
= 136 мм.
Шаг и диаметр горизонтальных поперечных стержней приопорного участка принимаем такими же, как для вертикальных хомутов, т.е. s1=100 мм, Asw1=154 мм2, отсюда
![]() Н/мм;
Н/мм;
![]()
h0 = 800 - 80 = 720 мм.
Проверим выражение qsw1b(h0-0,5x1) = 446,6·300(720-0,5·139)=
= 87,2·106 Н·мм < ![]() Н·мм.
Следовательно,
qsw
оставим без изменения.
Н·мм.
Следовательно,
qsw
оставим без изменения.
Проверим условие (173):
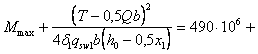
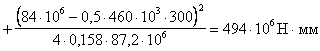 <
<
< RsAs(ho-0,5x1)=365·3217(720-0,5·139)=763,8·106 Н·мм,
т.е. верхней продольной арматуры из условия прочности установлено достаточно.
Из условия (176) проверим прочность по горизонтальной поперечной арматуре, расположенной на приопорном участке:
qsw1b(h0 -
0,5x1) = 446,6·300(720-0,5·139)=87,2·106
Н·мм > ![]() кН·м,
кН·м,
т.е. горизонтальной поперечной арматуры на приопорном участке установлено достаточно.
Как видно из черт. 61, б, д, в сечении с наибольшим пролетным изгибающим моментом имеет место крутящий момент, поэтому следует проверить прочность по продольной арматуре, установленной у нижней растянутой грани в средней части пролета ригеля, из условия (174).
Для этой части ригеля, два верхних стержня Æ 32 оборваны, и поэтому, согласно черт: 61, а, имеем A/sw = 1609 мм2 (2 Æ 32); а/ = 62 мм; As1 = 1388 мм2 (2 Æ 20 + 2 Æ22); а = 68 мм.
Определим
высоту сжатой зоны х1, принимая Rb = 13 МПа (т.е. при ![]() =0,9, поскольку ветровая нагрузка не учитывается):
=0,9, поскольку ветровая нагрузка не учитывается):
![]() <
0.
<
0.
Принимаем х1 = 2а', отсюда h0 - 0,5 x1 = h - a - a' = 800 - 68 - 62 = 670 мм.
Горизонтальные поперечные стержни в средней части пролета принимаем диаметром 14 мм (Аsw1 = 154 мм2) и с шагом s1 = 200 мм, отсюда
![]() Н/мм.
Н/мм.
Из черт. 61, б, д имеем:
![]() кН·м;
кН·м;
Мmax = 321 кН·м.
Проверим условие (174):
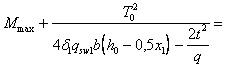
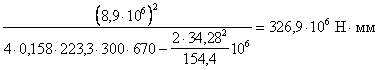 <
<
< RsAs1 (h0 - 0,5x1) = 365·1388·670=339,4·106 Н·мм,
т.е. нижней продольной арматуры из условия прочности установлено достаточно.
Определим,
на каком расстоянии lх от нулевой точки эпюры
Т можно допустить шаг горизонтальных
поперечных стержней 200 мм, используя условие (176). Принимая Т=tlx, имеем qsw1b(h0 - 0,5 x1) = ![]() , отсюда
, отсюда
![]()
Следовательно,
шаг горизонтальных стержней 100 мм можно допустить на приопорных участках
ригеля длиной 2,45-1,47
![]() 1 м.
1 м.
Пример 47. Дано: балка перекрытия с поперечным
сечением - по черт. 62, а;
расположение нагрузок, эпюры изгибающих и крутящих моментов,
а также эпюра поперечных сил - по черт. 62, б; бетон тяжелый класса В25 (Rb = 13 МПа при ![]() = 0,9); продольная и поперечная арматура класса
А-III (Rs
= Rsc = 365 МПа; Rsw
- 290 МПа).
= 0,9); продольная и поперечная арматура класса
А-III (Rs
= Rsc = 365 МПа; Rsw
- 290 МПа).
Требуется проверить прочность балки на совместное действие кручения и изгиба.
Расчет. Разбиваем поперечное сечение на два прямоугольника размерами 200х400 и 350х400 мм и проверяем условие (184):
![]()
= 84,5·106 Н·мм > Т = 40 кН·м.
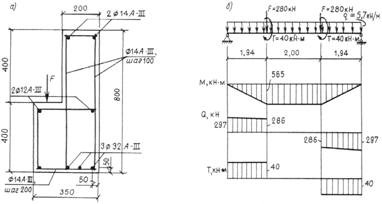
Черт. 62. К примеру расчета 47
Из черт. 62, а имеем h0=800-50=750 мм.
Сначала проверим прочность пространственного сечения по 2-й схеме согласно п. 3.90. При этом, поскольку сосредоточенные силы, приложенные посередине высоты сечения, вызывают отрыв растянутой зоны балки, учтем, что часть вертикальных хомутов воспринимает отрывающую силу, равную согласно п. 3.97:
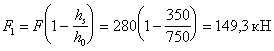
(где hs = 400 - 50 = 350 мм).
Усилие на единицу длины балки в вертикальных хомутах, расположенных у правой грани, от действия отрывающей силы F определим, распределяя отрывающую силу на две ветви хомутов и принимая ширину площадки опирания силы F b = 300 мм, тогда
а = 2hs + b = 2·350 + 300 = 1000 мм = 1 м,
т.е.
![]()
Таким образом, учитываемая при расчете пространственного сечения величина qsw2 при Аsw2 = 154 мм2 (1Æ14) и s2 = 100 мм (см. черт. 62, а) будет равна:
![]()
Согласно черт. 58, в и 62, а, принимаем bf,min = 200 мм, h = 800 мм, bov=0, As2 = 1071 мм2 (1Æ32 + 1Æ12+1Æ14).
Тогда значение с2 будет равно:
Пространственное сечение располагаем у опоры балки. Поскольку с2 < 1,94 м, т. е. пространственное сечение не выходит за пределы участка с ненулевыми значениями Т, оставляем с2 = 1,2 м.
Расчетные
значения Q и T принимаем на расстоянии ![]() от опоры, т.е.
от опоры, т.е. ![]() кН; Т = 40 кН·м.
кН; Т = 40 кН·м.
Поскольку RsAs2 = 365·1071 = 391·103 Н < 2qsw2h = 2·372·800=595·103 Н, оставляем RsAs2 = 391 кН.
Высоту сжатой зоны х2 определяем как для прямоугольного сечения согласно п. 3.20, принимая для данной схемы h0 = b0 = 200 -50 = 150 мм и b = h = 800 мм (сжатый свес полки не учитывается).
Поскольку а' = 50 мм составляет значительную долю от h0 = 150 мм, значение х2 определяем без учета сжатой арматуры:
![]() мм < а'
= 50 мм.
мм < а'
= 50 мм.
Проверяем условие (187), принимая bow = bo = 150 мм:
![]()
![]()
![]() >
>
> Т + 0,5 Qbf,min = 40 + 0,5 × 293,5 × 0,2 = 69,35 кН×м,
т. е. прочность по 2-й схеме обеспечена.
Проверяем прочность пространственного сечения по 1-й схеме согласно п. 3.89. Принимаем b'f = b = 200мм; bf= 350мм; Аs1 = 2526 мм2 (3Æ32 + 1Æ12); А¢s1 = 308 мм2 (2Æ14); Аsw1 = 154 мм2 (1Æ14); s1 = 200 мм.
Определяем длину проекции c1:
c1 = 2h + 2bf + b'f ‑ 2b =
= 2 × 800 + 2 × 350 + 200 ‑ 2 × 200 = 2100 мм.
Пространственное
сечение располагаем на участке между опорой и первым грузом у места приложения
этого груза. Поскольку c1 > 1,94 м, т.е. пространственное сечение
выходит за пределы балки, принимаем c1 = 1,94м.
Расчетные значения М и Т принимаем на расстоянии ![]() от опоры, т.е.
от опоры, т.е. ![]() кН×м;
Т = 40 кН×м.
кН×м;
Т = 40 кН×м.
Высоту сжатой зоны определяем как для прямоугольного сечения:
![]() ,
,
при этом х1 = 311 мм < xR ho = 0,604 × 750 = 453 мм (где xR ‑ см. табл. 18);
![]() .
.
Поскольку 2qsw1 bf + ![]() = 2 ×
223 ×
350 × +
= 2 ×
223 ×
350 × + ![]() = 636,2 × 103 H < Rs As1 = 365 × 2526 = 922 × 103 H, принимаем Rs As1 = 636,9 × 103 H.
= 636,2 × 103 H < Rs As1 = 365 × 2526 = 922 × 103 H, принимаем Rs As1 = 636,9 × 103 H.
Проверяем условие (185), приняв how = ho = 750 мм:
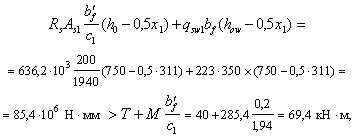
т. е. прочность сечения по 1-й схеме обеспечена.
Расчет железобетонных элементов
на местное действие нагрузок
РАСЧЕТ НА МЕСТНОЕ СЖАТИЕ
3.93(3.39). При расчете на местное сжатие (смятие) элементов без поперечного армирования должно удовлетворяться условие
![]() , (194)
, (194)
где N — продольная сжимающая сила от местной нагрузки;
Aloc1 — площадь смятия (см. черт. 63);
y — коэффициент, принимаемый равным:
при равномерном распределении местной нагрузки на площади смятия — 1,0;
при неравномерном распределении местной нагрузки на площади смятия (под концами балок, прогонов, перемычек) — 0,75;
Rb, loc ¾ расчетное сопротивление бетона смятию, определяемое по формуле
Rb, loc = ajb Rb, (195)
здесь ajb ³ 1,0;
a = 1,0 для бетона класса ниже В25;
a = 13,5 Rbt /Rb для бетона класса В25 и выше;
jb = ![]() ,
,
но не более следующих значений:
при схеме приложения нагрузки по черт. 63, а, в, г, е, и для бетона:
тяжелого, мелкозернистого и легкого классов:
выше В7,5 ....................... 2,5
В3,5; В5; В7,5 ................. 1,5
легкого класса В2,5 ........ 1,2
при схеме приложения нагрузки по черт. 63, б, д, ж независимо от вида и класса бетона ¾ 1,0;
Rb, Rbt — принимаются как для бетонных конструкций (см. поз. 5 табл. 9);
Aloc2 — расчетная площадь смятия, определяемая в соответствии с п. 3.94.
Если условие (194) не удовлетворяется, рекомендуется применять косвенное армирование в виде сварных сеток и рассчитывать элемент в соответствии с п. 3.95.
3.94(3.40). В расчетную площадь Aloc2 включается участок, симметричный по отношению к площади смятия (черт. 63). При этом должны выполняться следующие правила:
при местной нагрузке по всей ширине элемента b в расчетную площадь включается участок длиной не более b в каждую сторону от границы местной нагрузки (черт. 63, а);
при местной краевой нагрузке по всей ширине элемента расчетная площадь Aloc2 равна площади смятия Aloc1 (черт. 63, б);
при местной нагрузке в местах опирания концов прогонов и балок в расчетную площадь включается участок шириной, равной глубине заделки прогона или балки, и длиной не более расстояния между серединами пролетов, примыкающих к балке (черт. 63, в);
если расстояние между балками превышает двойную ширину элемента, длина расчетной площади определяется как сумма ширины балки и удвоенной ширины элемента (черт. 63, г);
при местной краевой нагрузке на угол элемента (черт. 63, д) расчетная площадь Aloc2 равна площади смятия Aloc1;
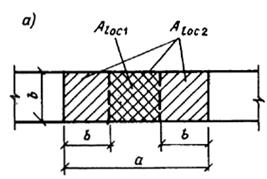
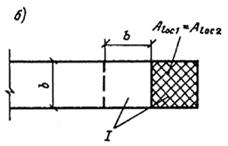
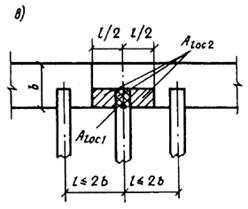
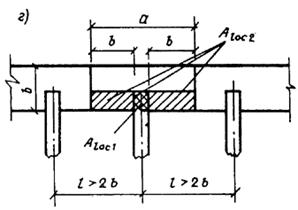
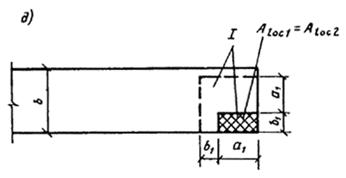
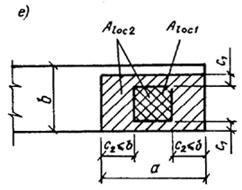
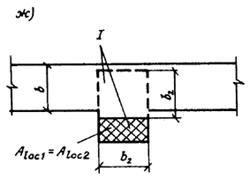
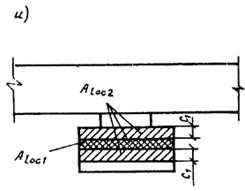
Черт. 63. Определение расчетной площади Aloc2 при расчете на местное сжатие при местной нагрузке
а ¾ по всей ширине элемента; б ¾ краевой по всей ширине элемента; в, г ¾ в местах опирания концов прогонов и балок; д — краевой на угол элемента; е — на часть длины и ширины элемента; ж — краевой в пределах выступа стены (пилястры); и — на сечение сложной формы; I — минимальная зона армирования сетками, при
которой косвенное армирование учитывается в расчете
при местной нагрузке, приложенной на части длины и ширины элемента, расчетная площадь принимается согласно черт. 63, е. При наличии нескольких нагрузок указанного типа расчетные площади ограничиваются линиями, преходящими через середину расстояний между точками приложения двух соседних нагрузок;
при местной краевой нагрузке, расположенной в пределах выступа стены (пилястры) или простенка таврового сечения, расчетная площадь Aloc2 равна площади смятия Aloc1 (черт. 63, ж);
при определении расчетной площади для сечений сложной формы не должны учитываться участки, связь которых с загруженным участком не обеспечена с необходимой надежностью (черт. 63, и).
Примечание. При местной нагрузке от балок, прогонов, перемычек и других элементов, работающих на изгиб, учитываемая в расчете глубина опоры при определении Aloc1 и Aloc2 принимается не более 20 см.
3.95(3.41). При расчете на местное сжатие элементов из тяжелого бетона с косвенным армированием в виде сварных поперечных сеток должно удовлетворяться условие
N £ R*b,loc Aloc1, (196)
где Aloc1 ¾ площадь смятия;
R*b,loc — приведенная призменная прочность бетона при расчете на местное сжатие, определяемая по формуле
R*b,loc = Rb jb + jmxy Rs,xy js, (197)
здесь Rs,xy , j, mxy ¾ обозначения те же, что в п. 3.57;
jb = ![]() , но не более 3,5;
, но не более 3,5;
js — коэффициент, учитывающий влияние косвенного армирования в зоне местного сжатия; для схем черт. 63, б, д, ж принимается js = 1,0, при этом косвенное армирование учитывается в расчете при условии, что поперечные сетки установлены на площади не менее ограниченной пунктирными линиями на соответствующих схемах черт. 63; для схем черт. 63, а, в, г, е, и коэффициент js определяется по формуле
![]() ,
,
Aef — площадь бетона, заключенного внутри контура сеток косвенного армирования, считая по их крайним стержням, для которой должно удовлетворяться условие Aloc1 < Aef £ Aloc2.
Если контур площади смятия выходит за пределы контура сеток косвенного армирования [например, на величину защитного слоя бетона арматуры сеток при расположении площади смятия у краев элемента (см. черт.63, а ‑ д, ж, и)], при определении значений Aloc1 и Aloc2 не учитывается площадь, занимаемая защитным слоем.
Наименьшую глубину заложения сеток косвенного армирования следует определять по формулам:
для схем загружения по черт. 63, в ‑ е
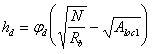 ; (198)
; (198)
для схем загружения по черт. 63, а, б, ж, и
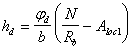 . (199)
. (199)
В формулах (198) и (199):
jd = 0,5 — при схемах загружения по черт. 63, а, е, и;
jd = 0,75 ¾ при схемах загружения по черт. 63, в, г;
jd = 1,0 — при схемах загружения по черт. 63, б, д, ж.
Число сеток принимается не менее двух. Кроме того, должны выполняться конструктивные требования п. 5.79. При этом, если в каком-либо направлении размеры ячейки сетки превышают 100 мм или 1/4 меньшей стороны сечения, стержни сетки этого направления не учитываются при определении коэффициента mху.
ПРИМЕРЫ РАСЧЕТА
Пример 48. Дано: стальная стойка, опираемая на железобетонный фундамент и центрально-нагруженная силой N = 1000 кН (черт. 64); фундамент из тяжелого бетона класса В 12,5 (Rb = 6,7 МПа при gb2 = 0,9).
Требуется проверить прочность бетона под стойкой на местное сжатие (смятие).
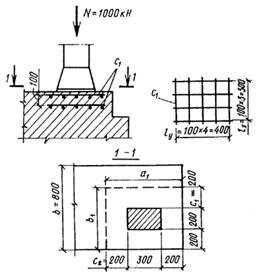
Черт. 64. К примеру расчета 48
Расчет производим в соответствии с указаниями пп. 3.93 и 3.94.
Расчетную площадь Аloc2 определяем в соответствии с черт. 63, е.
Согласно черт. 64, имеем c1 = 200 мм < b = 800 мм; a1 = 200 × 2+300 = 700 мм; b1 = 200 × 2+200 = 600 мм; Аloc2 = a1 b1 = 700 × 600 = 420000 мм2.
Площадь смятия равна Аloc1 = 300 × 200 = 60000 мм2. Поскольку класс бетона ниже В25, a = 1,0.
Коэффициент jb равен:
![]()
Определяем расчетное сопротивление бетона смятию по формуле (195), принимая rb с учетом gb9 = 0,9 (см. табл. 9) как для бетонной конструкции: rb = 6,7 × 0,9 = 6,03 МПа:
Rb, loc = ajb Rb = 1 × 9 × 6,03 = 11,5 МПа
(где ajb = 1 × 1,9 = 1,9 > 1,0).
Проверяем условие (194), принимая y = 1,0 как при равномерном распределении местной нагрузки, тогда
![]() = 1 × 11,5 × 60000 = 690000 H
= 690 кН < N
= 1000 кН,
= 1 × 11,5 × 60000 = 690000 H
= 690 кН < N
= 1000 кН,
т. е. прочность бетона на местное сжатие не обеспечена, и поэтому необходимо применить косвенное армирование. Принимаем косвенное армирование в виде сеток из арматурной проволоки класса Вр-1, диаметром 3 мм, ячейкой 100´100 мм и шагом по высоте s = 100 мм (Rs,xy = 375 МПа).
Проверяем прочность согласно п. 3.95. Так как jb = 1,9 < 3,5, в расчет вводим jb = 1,9.
Коэффициент косвенного армирования сетками mxу определяем по формуле (99).
Из черт. 64 имеем: пx = 5; lx = 300 мм; пy = 4; ly = 400мм; Аsx = Аsy = 7,1 мм2 (Æ3); Аef = lx lу = 300 × 400 = 120000 мм2 > Aloc1 = 60 000 мм2, тогда
![]()
По формулам (101) и (100) определяем y и j:
![]()
![]()
Коэффициент js равен:
js = 4,5 ‑ 3,5 Aloc1/Aef = 4,5 ‑ 3,5 × 60000/120000 = 2,75.
Приведенную прочность бетона R*b,loc определяем по формуле (197):
R*b,loc = Rb jb + jmxy Rs,xy js =
= 6,7 × 1,9+ 3,69 × 0,00183 × 375 × 2,75 = 19,7 МПа.
Проверяем условие (196):
R*b,loc Aloc1 = 19,7 × 60000 = 1182 × 103 H > N = 1000 кН,
т. е. прочность бетона обеспечена.
Определяем наименьшую глубину заложения сеток по формуле (198), принимая jd = 0,5:
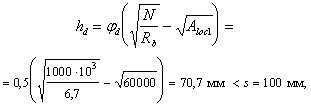
т. е. достаточно установить две сетки.
РАСЧЕТ НА ПРОДАВЛИВАНИЕ
3.96(3.42). Расчет на продавливание плитных конструкций (без поперечной арматуры) от действия сил, равномерно распределенных на ограниченной площади, должен производиться из условия
F £ aRbt um ho, (200)
где F ¾ продавливающая сила;
a — коэффициент, принимаемый равным для бетона:
тяжелого ........................ 1,00
мелкозернистого .......... 0,85
легкого .......................... 0,80
um ¾ среднеарифметическое значение периметров верхнего и нижнего оснований пирамиды, образующейся при продавливании в пределах рабочей высоты сечения.
При определении um и F предполагается, что продавливание происходит по боковой поверхности пирамиды, меньшим основанием которой служит площадь действия продавливающей силы, а боковые грани наклонены под углом 45° к горизонтали черт.65, а).
Продавливающая сила F принимается равной силе, действующей на пирамиду продавливания, за вычетом нагрузок, приложенных к большему основанию пирамиды продавливания (считая по плоскости расположения растянутой арматуры) и сопротивляющихся продавливанию.
Если схема опирания такая, что продавливание может происходить только по поверхности пирамиды с углом наклона боковых граней более 45° [например, в свайных ростверках (черт. 65, б)], тогда правая часть условия (200) определяется для фактической пирамиды продавливания с умножением на ho/с (где с — длина горизонтальной проекции боковой грани пирамиды продавливания). При этом значение несущей способности принимается не более значения, соответствующего пирамиде при с = 0,4hо.
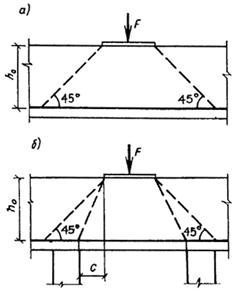
Черт. 65. Схема пирамиды продавливания при угле наклона ее боковых граней к горизонтали
а ¾ 45°; б ¾ более 45°
При установке в пределах пирамиды продавливания хомутов, нормальных к плоскости плиты, расчет должен производиться из условия
F £ Fb + 0,8 Fsw, (201)
но не более 2Fb,
где Fb — правая часть условия (200);
Fsw = 175 SAsw ¾ сумма всех поперечных усилий, воспринимаемых хомутами, пересекающими боковые грани пирамиды продавливания (175 МПа ¾ предельное напряжение в хомутах).
При учете поперечной арматуры значение Fsw должно быть не менее 0,5 Fb.
Допускается учитывать в расчете и меньшее значение Fsw при замене правой части условия (201) на 2,8Fsw, но не менее Fb.
При расположении хомутов на ограниченном участке вблизи сосредоточенного груза производится дополнительный расчет на продавливание пирамиды с верхним основанием, расположенным по контуру участка, с поперечной арматурой, из условия (200) без учета поперечной арматуры.
Поперечная арматура должна удовлетворять требованиям п. 5.75.
РАСЧЕТ НА ОТРЫВ
3.97(3.43). Расчет железобетонных элементов на отрыв от действия нагрузки, приложенной к его нижней грани или в пределах высоты его сечения (черт. 66), должен производиться из условия
 (202)
(202)
где F — отрывающая сила;
hs ¾ расстояние от уровня передачи отрывающей силы на элемент до центра тяжести сечения продольной арматуры S; при передаче нагрузки через монолитно связанные балки или консоли принимается, что нагрузка передается на уровне центра тяжести сжатой зоны элемента, вызывающего отрыв;
SRswАsw ¾ сумма поперечных усилий, воспринимаемых хомутами, устанавливаемыми дополнительно сверх требуемых по расчету наклонного или пространственного сечения согласно пп. 3.31¾3.39, 3.86, 3.87 и 3.90; эти хомуты располагаются по длине зоны отрыва, равной:
а = 2 hs + b, (203)
здесь b ¾ ширина площадки передачи отрывающей силы F.
При равномерно распределенной нагрузке q, приложенной в пределах высоты сечения, необходимая интенсивность хомутов увеличивается на величину q(1 ‑ hs/ho)/Rsw.
3.98. Входящие углы в растянутой зоне элементов, армируемые пересекающимися продольными стержнями (черт. 67), должны иметь поперечную арматуру, достаточную для восприятия:
а) равнодействующей усилий в продольных растянутых стержнях, не заведенных в сжатую зону, равной:
![]() ; (204)
; (204)
б) 35 % равнодействующей усилий во всех продольных растянутых стержнях, равных:
![]() . (205)
. (205)
Необходимая по
расчету из этих условий поперечная арматура должна быть расположена по длине s = h tg ![]() b.
b.
Сумма проекций усилий в поперечных стержнях (хомутах), располагаемых по этой длине, на биссектрису угла должна составлять не менее суммы F1 + f2,
т. е. SRsw Asw cosq ³ F1 + F2. (206)
В формулах (204) ¾ (206):
As ¾ площадь сечения всех продольных растянутых стержней;
Аs1 ¾ площадь сечения продольных растянутых стержней, не заанкеренных в сжатой зоне;
b ¾ входящий угол в растянутой зоне элемента;
SAsw ¾ площадь сечения поперечной арматуры в пределах длины s;
q — угол наклона поперечных стержней к биссектрисе угла b.
Черт. 66. Схема для определения длины зоны отрыва
а ¾ при примыкании балок; б ¾ то же, консолей; I ¾ центр тяжести сжатой зоны сечения примыкающего элемента
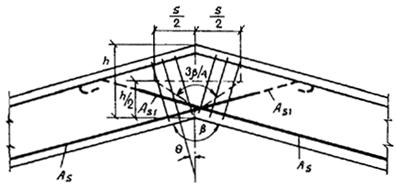
Черт. 67. Армирование входящего угла, расположенного в растянутой зоне железобетонного элемента
Расчет коротких консолей
3.99 (3.34). Расчет коротких консолей колонн [l1 £ 0,9 h0; (черт. 68)] на действие поперечной силы для обеспечения прочности по наклонной сжатой полосе между грузом и опорой должен производиться из условия
Q £ 0,8 Rb b lsup sin2 q (1 + 5 amw), (207)
в котором правая часть принимается не более 3,5 Rbt b ho и не менее 2,5 Rbt b ho.
В условии (207):
lsup ¾ длина площадки опирания нагрузки вдоль вылета консоли;
q —
угол наклона расчетной сжатой полосы к горизонтали 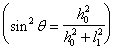 ;
;
![]() —
коэффициент армирования хомутами, расположенными по высоте консоли;
—
коэффициент армирования хомутами, расположенными по высоте консоли;
здесь sw — расстояние между хомутами, измеренное по нормали к ним.
При расчете учитываются хомуты горизонтальные и наклонные под углом не более 45° к горизонтали.
Напряжение сжатия в местах передачи нагрузки на консоль не должно превышать Rb,loc (см. п. 3.93).
Для коротких консолей, входящих в жесткий узел рамной конструкции с замоноличиванием стыка, значение lsup в выражении (207) принимается равным вылету консоли l1, если при этом выполняются условия М/Q ³ 0,3 м и lsup/l1 ³ 2/3 (где М и Q — соответственно момент, растягивающий верхнюю грань ригеля, и поперечная сила в нормальном сечении ригеля по краю консоли). В этом случае правая часть условия (207) принимается не более 5Rthbho.
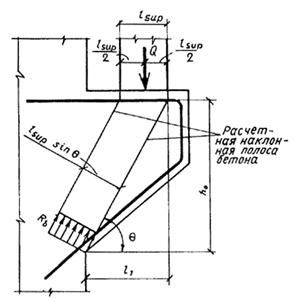
Черт. 68. Расчетная схема для короткой консоли при действии поперечной силы
При шарнирном опирании на короткую консоль сборной балки, идущей вдоль вылета консоли, при отсутствии специальных выступающих закладных деталей, фиксирующих площадку опирания (черт. 69), значение lsup в условии (207) принимается равным 2/3 длины фактической площадки опирания.
Поперечное армирование коротких консолей должно удовлетворять требованиям п. 5.77.
Черт. 69. Расчетная схема для короткой консоли при шарнирном опирании сборной балки, идущей вдоль вылета консоли
3.100. При шарнирном опирании балки на консоль колонны продольная арматура консоли проверяется из условия
![]() , (208)
, (208)
где l1, ho ¾ см. черт. 68.
При этом продольная арматура консоли должна быть доведена до свободного конца консоли и иметь надлежащую анкеровку (см. пп. 5.44 и 5.45).
При жестком соединении ригеля и колонны с замоноличиванием стыка и привариванием нижней арматуры ригеля к арматуре консоли через закладные детали продольная арматура консоли проверяется из условия
![]() , (209)
, (209)
где l1, ho — соответственно вылет и рабочая высота короткой консоли;
Ns — горизонтальное усилие, действующее на верх консоли от ригеля, равное:
![]() (210)
(210)
и принимаемое не более 1,4 kf lw Rwf + 0,3 Q (где kf и lw — соответственно высота и длина углового шва приваривания закладных деталей ригеля и консоли; Rf ¾ расчетное сопротивление угловых швов срезу по металлу шва, определяемое согласно СНиП II-23-81, при электродах Э42 Rwf = 180 МПа; 0,3 — коэффициент трения стали по стали), а также не более Rsw аsw (где Rsw и аsw — соответственно расчетное сопротивление и площадь сечения верхней арматуры ригеля).
В формулах (209) и (210):
M, Q — соответственно изгибающий момент и поперечная сила в нормальном сечении ригеля по краю консоли; если момент М растягивает нижнюю грань ригеля, значение М учитывается в формуле (210) со знаком "минус";
lsup — фактическая длина площадки опирания нагрузки вдоль вылета консоли;
hob — рабочая высота ригеля.
ПРИМЕРЫ РАСЧЕТА
Пример 49. Дано: на короткую консоль колонны опирается свободно лежащая сборная балка (черт. 70), идущая вдоль вылета консоли; длина площадки опирания lsup,f = 300 мм; ширина консоли (колонны) b = 400 мм; соответственно высота и вылет консоли h = 700 мм, l1 = 350 мм; бетон колонны тяжелый класса В25 (Rb = 13 МПа, Rbt = 0,95 МПа при gb2 = 0,9; Еb = 27 × 103 МПа); продольная арматура класса А-III (Rs = 365 МПа); нагрузка на консоль Q = 700 кН.
Требуется проверить прочность консоли на действие поперечной силы и определить площадь сечения продольной арматуры и хомутов.
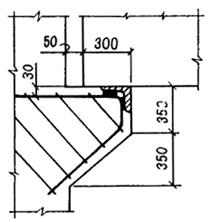
Черт. 70. К примеру расчета 49
Расчет. ho = h ‑ а = 700 ‑ 30 = 670 мм. Поскольку 3,5 Rbt bho = 3,5 × 0,95 × 400 × 670 = 891,1 × 103 H = 891,1 кН > Q = 700 кН и в то же время 2,5 Rbt bho = 2,5 × 0,95 × 400 × 670 = 636,5 кН <Q = 700 кН, прочность консоли проверяем из условия (207).
Согласно п. 3.99, расчетную длину площадки опирания нагрузки принимаем равной:
lsup = 2/3 lsup, f = 2/3 × 300 = 200 мм.
Согласно п. 5.77, принимаем шаг хомутов равным
sw = 150 мм < ![]() = 175 мм.
= 175 мм.
При двухветвевых хомутах диаметром 10 мм имеем Аsw = 157 мм2, тогда
![]() ;
;
![]() ;
;
![]()
0,8 Rb blsup sin2q (1 + 5 amw) = 0,8 × 13 × 400 × 200 ´
´ 0,786 (1+5×7,4 × 2,62 × 10-3) = 717 × 103 H > Q = 700 кН,
т. е. прочность консоли по поперечной силе обеспечена.
Из условия (208) определим необходимую площадь сечения продольной арматуры консоли:
![]()
Принимаем 3 Æ 22 (As = 1140 мм2).
Расчет закладных деталей и соединений элементов
РАСЧЕТ ЗАКЛАДНЫХ ДЕТАЛЕЙ
3.101 (3.44). Расчет нормальных анкеров, приваренных в тавр к плоским элементам стальных закладных деталей, на действие изгибающих моментов, нормальных и сдвигающих сил от статической нагрузки, расположенных в одной плоскости симметрии закладной детали (черт. 71), должен производиться по формуле
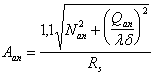 , (211)
, (211)
где Aan — суммарная площадь поперечного сечения анкеров наиболее напряженного ряда;
Nan ¾ наибольшее растягивающее усилие в одном ряду анкеров, равное:
![]() (212)
(212)
Qan ¾ сдвигающее усилие, приходящееся на один ряд анкеров, равное:
![]() (213)
(213)
N¢an — наибольшее сжимающее усилие в одном ряду анкеров, определяемое по формуле
![]() (214)
(214)
В формулах (211) ¾ (214):
М, N, Q — соответственно момент, нормальная и сдвигающая силы, действующие на закладную деталь; момент определяется относительно оси, расположенной в плоскости наружной грани пластины и проходящей через центр тяжести всех анкеров;
z ¾ расстояние между крайними рядами анкеров;
nan — число рядов анкеров вдоль направления сдвигающей силы; если не обеспечивается равномерная передача сдвигающей силы Q на все ряды анкеров, то при определении сдвигающего усилия Qan учитывается не более четырех рядов;
l — коэффициент, определяемый для анкерных стержней диаметром 8 — 25 мм для тяжелого и мелкозернистого бетонов классов В12,5 — В50 и легкого бетона классов В12,5 — В30 по формуле
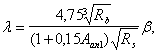 (215)
(215)
но принимаемый не более 0,7; для тяжелого и мелкозернистого бетонов класса выше В50 коэффициент l принимается как для класса В50, а для легкого бетона класса выше В30 — как для класса В30. Для тяжелого бетона коэффициент l можно определять по табл. 28.
В формуле (215):
Rb, Rs, ¾ в МПа;
при определении Rb коэффициент gb2 (см. п. 3.1) принимается равным 1,0;
Aan1 ¾ площадь сечения анкерного стержня наиболее напряженного ряда, см2;
b ¾ коэффициент, принимаемый равным для бетона:
тяжелого ................................ 1,0
мелкозернистого групп:
А ............................................. 0,8
Б и В ....................................... 0,7
легкого .................................. rm/2300
(rm ¾ средняя плотность
бетона, кг/м3);
d ¾ коэффициент, определяемый по формуле
![]() (216)
(216)
но принимаемый не менее 0,15;
здесь w = 0,3 ![]() при N¢an > 0 (имеется прижатие);
при N¢an > 0 (имеется прижатие);
w = 0,6 ![]() при N¢an £
0 (нет прижатия);
при N¢an £
0 (нет прижатия);
если растягивающие усилия в анкерах отсутствуют, то коэффициент d принимается равным 1,0.
Площадь сечения анкеров остальных рядов должна приниматься равной площади сечения анкеров наиболее напряженного ряда.
В формулах (212) и (214) нормальная сила N считается положительной, если направлена от закладной детали (см. черт. 71), и отрицательной — если направлена к ней. В случаях, когда нормальные усилия Nan и N¢an, а также сдвигающее усилие Qan при вычислении по формулам (212) ¾ (214) получают отрицательные значения, в формулах (211), (213) и (216) их принимают равными нулю. Кроме того, если Nan получает отрицательное значение, в формуле (213) принимается N¢an =N.
При расположении закладной детали на верхней (при бетонировании) поверхности изделия коэффициент l уменьшается на 20 %, а значение N¢an в формуле (213) принимается равным нулю.
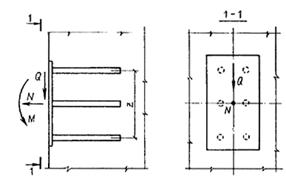
Черт. 71. Схема усилий, действующих на закладную деталь
3.102. Расчет нормальных анкеров закладных деталей на действие расположенных в двух плоскостях симметрии закладной детали изгибающих моментов и сдвигающих сил, а также нормальной силы и крутящих моментов выполняется в соответствии с "Рекомендациями по проектированию стальных закладных деталей для железобетонных конструкций" (М., Стройиздат, 1984).
3.103(3.45). В закладной детали с анкерами, приваренными внахлестку под углом от 15 до 30° (см. п. 5.111), наклонные анкера, располагаемые симметрично относительно плоскости действия сдвигающей силы, рассчитываются на действие этой сдвигающей силы (при Q > N, где N ¾ отрывающая сила) по формуле
![]() (217)
(217)
где Aan,inc ¾ суммарная площадь поперечного сечения наклонных анкеров;
Nan ¾ см. п. 3.101.
При этом должны устанавливаться нормальные анкера, рассчитываемые по формуле (211) при d = 1,0 и при значениях Qan, равных 0,1 сдвигающего усилия, определяемого по формуле (213). Допускается уменьшать площадь сечения наклонных анкеров за счет передачи на нормальные анкера части сдвигающей силы, равной Q ‑ 0,9 Rs Aan,inc. В этом случае d определяется по формуле (216).
Таблица 28
|
Диаметр |
Значения коэффициента l для расчета нормальных анкеров закладных деталей в зависимости от класса тяжелого бетона и арматуры |
||||||||||||||||||
|
анкера, |
В15 |
B20 |
B25 |
B30 |
B40 |
³ B50 |
|||||||||||||
|
мм |
А-I |
A-II |
A-III |
А-I |
A-II |
A-III |
А-I |
A-II |
A-III |
А-I |
A-II |
A-III |
А-I |
A-II |
А-III |
А-I |
A-II |
A-III |
|
|
8 |
0,60 |
¾ |
0,48 |
0,66 |
¾ |
0,53 |
0,70 |
¾ |
0,57 |
0,70 |
¾ |
0,60 |
0,70 |
¾ |
0,66 |
0,70 |
¾ |
0,70 |
|
|
10 |
0,58 |
0,52 |
0,45 |
0,64 |
0,57 |
0,50 |
0,69 |
0,62 |
0,54 |
0,70 |
0,65 |
0,57 |
0,70 |
0,70 |
0,63 |
0,70 |
0,70 |
0,66 |
|
|
12 |
0,55 |
0,50 |
0,43 |
0,61 |
0,55 |
0,48 |
0,66 |
0,59 |
0,52 |
0,70 |
0,62 |
0,55 |
0,70 |
0,69 |
0,60 |
0,70 |
0,70 |
0,63 |
|
|
14 |
0,53 |
0,47 |
0,41 |
0,58 |
0,52 |
0,46 |
0,63 |
0,56 |
0,49 |
0,66 |
0,59 |
0,52 |
0,70 |
0,65 |
0,57 |
0,70 |
0,69 |
0,60 |
|
|
16 |
0,50 |
0,45 |
0,39 |
0,55 |
0,49 |
0,43 |
0,59 |
0,53 |
0,47 |
0,63 |
0,56 |
0,49 |
0,69 |
0,62 |
0,54 |
0,70 |
0,65 |
0,57 |
|
|
18 |
0,47 |
0,42 |
0,37 |
0,52 |
0,46 |
0,41 |
0,56 |
0,50 |
0,44 |
0,59 |
0,53 |
0,46 |
0,65 |
0,58 |
0,51 |
0,68 |
0,61 |
0,54 |
|
|
20 |
0,44 |
0,39 |
0,34 |
0,49 |
0,44 |
0,38 |
0,52 |
0,47 |
0,41 |
0,55 |
0,50 |
0,43 |
0,61 |
0,54 |
0,48 |
0,64 |
0,58 |
0,50 |
|
|
22 |
0,41 |
0,37 |
0,32 |
0,46 |
0,41 |
0,36 |
0,49 |
0,44 |
0,39 |
0,52 |
0,46 |
0,41 |
0,57 |
0,51 |
0,45 |
0,60 |
0,54 |
0,47 |
|
|
25 |
0,37 |
0,33 |
0,29 |
0,41 |
0,37 |
0,32 |
0,44 |
0,40 |
0,35 |
0,47 |
0,42 |
0,37 |
0,51 |
0,46 |
0,40 |
0,54 |
0,49 |
0,43 |
|
Примечания: 1. Для бетона класса В 12,5 коэффициент l следует уменьшать на 0,02 по сравнению с коэффициентом l для бетона класса В15.
2. Значения коэффициента l приведены при gbi = 1,00.
3.104. На приваренные к пластине упоры из полосовой стали или арматурных коротышей (см. п. 5.114) можно передавать не более 30% сдвигающей силы, действующей на деталь при напряжениях в бетоне под упорами, равных Rb. При этом значение сдвигающей силы, передаваемой на анкера закладной детали, соответственно снижается.
3.105(3.46). Конструкция сварных закладных деталей с приваренными к ним элементами, передающими нагрузку на закладные детали, должна обеспечивать включение в работу анкерных стержней в соответствии с принятой расчетной схемой. Внешние элементы закладных деталей и их сварные соединения рассчитываются согласно СНиП II-23-81. При расчете пластин и фасонного проката на отрывающую силу рекомендуется принимать, что они шарнирно соединены с нормальными анкерными стержнями. Если элемент, передающий нагрузку, приваривается к пластине по линии расположения одного из рядов анкеров, при расчете отрывающую силу рекомендуется уменьшать на величину пaАan1Rs (где na — число анкеров в данном ряду).
Кроме того, толщину пластины t расчетной закладной детали, к которой привариваются втавр анкера, следует проверять из условия
t ³ 0,25 ![]() , (218)
, (218)
где dan — диаметр анкерного стержня, требуемый по расчету;
Rsq — расчетное сопротивление прокатной стали закладной детали сдвигу, равное 0,58 Ry (где Ry ¾ см. СНиП II-23-81).
Для типов сварных соединений, обеспечивающих большую зону включения пластины в работу при вырывании из нее анкерного стержня (см. поз. 6 табл. 52), возможна корректировка условия (218) с целью уменьшения толщины пластины. При действии на закладную деталь с уменьшенной толщиной пластины сдвигающей силы Q суммарная площадь сечения (перпендикулярного действию этой силы) пластины с приваренными к ней элементами в зоне расположения анкерных стержней вдоль силы Q принимается не менее площади сечения пластины толщиной, определяемой по формуле (218)
3.106. При выполнении условия
N¢an £ 0, (219)
где N¢an — см. п. 3.101, т. е. когда все нормальные анкера растянуты, производят расчет на выкалывание бетона следующим образом:
а) для нормальных анкеров с усилением на концах (см. п. 5.113) ¾ из условия
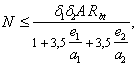 (220)
(220)
где А — площадь проекции на плоскость, нормальную к анкерам, поверхности выкалывания, идущей от усилений анкеров (краев анкерных пластин или высаженных головок) под углом 45° к осям анкеров; при эксцентриситете силы N относительно центра тяжести анкеров eo = M/N размер проекции поверхности выкалывания в направлении этого эксцентриситета уменьшается на величину, равную 2eo, при соответствующем смещении наклонной грани поверхности выкалывания (черт. 72); площади анкерных пластин или высаженных головок, расположенных на поверхности выкалывания, не учитываются;
d1 ¾ коэффициент, принимаемый равным: для тяжелого и мелкозернистого бетонов — 0,5; для легкого бетона — 0,4;
d2 — коэффициент, принимаемый равным:
при
![]() или
или ![]() d2 = 1,0;
d2 = 1,0;
при ![]() d2 = 1,2.
d2 = 1,2.
При этом, если часть стержня длиной а расположена в зоне бетона при 0,25 £ sbc/Rb £ 0,75, d2 определяется по формуле
d2 = 1
+ 0,2 ![]() , (221)
, (221)
здесь la — длина анкерного стержня;
сжимающие напряжения в бетоне sbc, перпендикулярные нормальному анкеру и распределенные по всей длине, определяются как для упругого материала по приведенному сечению от постоянно действующих нагрузок при коэффициенте надежности по нагрузке, равном 1,0;
a1, a2 — размеры проекции поверхности выкалывания;
e1, e2 — эксцентриситеты силы N относительно центра тяжести площади А в направлении соответственно размеров а1 и a2;
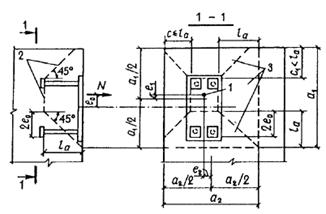
Черт. 72. Схема выкалывания бетона анкерами закладной детали с усилениями на концах при N¢an £ 0
1 ¾ точка приложения нормальной силы N; 2 ¾ поверхность выкалывания; 3 — проекция поверхности выкалывания на плоскость, нормальную к анкерам
б) для анкеров без усиления на концах расчет производится из условия
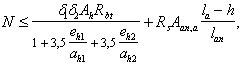 (222)
(222)
где Ah — то же, что и А, если поверхность выкалывания проходит на расстоянии h от пластины закладной детали (черт. 73);
ah1, ah2 ¾ размеры проекции поверхности выкалывания;
eh1, eh2 — эксцентриситеты силы N относительно центра тяжести площади Ah, в направлении соответственно размеров ah1 и ah2;
Аan,a ¾ площадь сечения всех анкеров, пересекающих поверхность выкалывания;
lan — длина зоны анкеровки (см. п. 5.44).
Условие (222) проверяется при различных значениях h, меньших длины анкеров или равных ей.
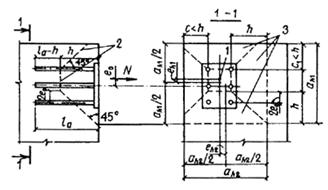
Черт. 73. Схема выкалывания бетона анкерами закладной детали без усилений на концах при N'an £ 0
1 ¾ точка приложения нормальной силы N; 2 ¾ поверхность выкалывания; 3 ¾ проекция поверхности выкалывания на плоскость, нормальную к анкерам
Если число
анкеров в направлении эксцентриситета больше двух, в условиях (220) и (222)
силу N можно уменьшить на
величину 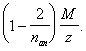
Если концы анкеров находятся вблизи поверхности бетона, противоположной пластине закладной детали, необходимо произвести дополнительную проверку условия (222) без учета последнего члена правой части условия при h, равном расстоянию от пластины до противоположной грани элемента, при этом часть площади Ah, расположенная между крайними рядами анкеров, не учитывается.
3.107. При выполнении условия N¢an > 0 и наличии усиления на концах анкеров расчет бетона на выкалывание (черт. 74) производится из условия
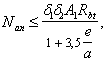 (223)
(223)
где Nan ¾ см. формулу (212);
A1 ¾ то же, что А в формуле (220), если поверхность выкалывания начинается от места усиления анкеров наиболее растянутого ряда (см. черт. 74);
е — эксцентриситет усилия N относительно центра тяжести площади А1 в направлении размера а.
Расчет на выкалывание можно не производить, если концы анкеров заведены за продольную арматуру, расположенную у противоположной от закладной детали грани колонны, а усиления анкеров в виде пластин или поперечных коротышей зацепляются за стержни продольной арматуры диаметром: при симметричном зацеплении — не менее 20 мм, при несимметричном — не менее 25 мм (черт. 75). В этом случае участок колонны между крайними рядами анкеров проверяется, согласно пп. 3.31 и 3.53, на действие поперечной силы, равной:
Q = Nan ![]() Qcol,
Qcol,
где Qcol ¾ поперечная сила на участке колонны, прилежащем к наиболее растянутому ряду анкеров закладной детали, определяемая с учетом усилий, действующих на закладную деталь.
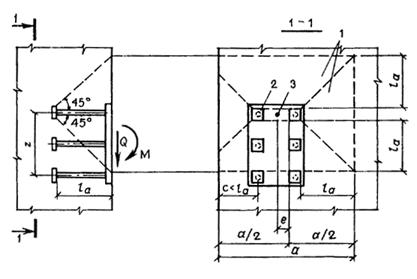
Черт. 74. Схема выкалывания бетона растянутыми анкерами закладной детали при N¢an > 0
1 — проекция поверхности выкалывания на плоскость, нормальную к анкерам; 2 — анкерная пластина; 3 — точка приложения усилия Nan
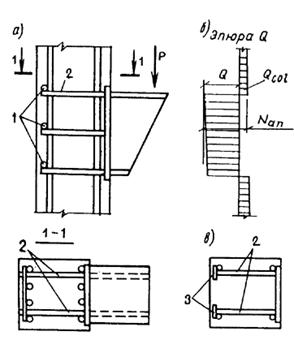
Черт. 75. Конструкция закладной детали, не требующей расчета на выкалывание
а — закладная деталь с коротышами, симметрично зацепленными за продольную арматуру колонны; б ¾ эпюра Q участка колонны с закладной деталью; в ¾ анкера закладной детали с анкерными пластинами, несимметрично зацепленными за продольную арматуру колонны; 1 — поперечные коротыши, приваренные контактной сваркой к анкерам; 2 ¾ анкера; 3 ¾ анкерные пластины
3.108. Если сдвигающая сила Q действует на закладную деталь по направлению к краю элемента (черт. 76), при отсутствии наклонных анкеров расчет на откалывание бетона производится из условия
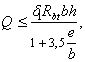 (224)
(224)
где d1 ¾ см. п. 3.106; при расположении закладной детали на верхней (при бетонировании) поверхности изделий из легких бетонов коэффициент d1 уменьшается на 20 %,
b ¾ ширина элемента, равная b = c1 + c2 + s (где c1 и c2 ¾ расстояния от крайних рядов анкеров до ближайших краев элемента в направлении, нормальном к сдвигающей силе, принимаемые не более h, s ¾ расстояние между крайними рядами анкеров в том же направлении);
h ¾ расстояние от наиболее удаленного ряда анкеров до края элемента в направлении сдвигающей силы Q, принимаемое не более толщины элемента b1 (см. черт. 76);
е ¾ эксцентриситет силы Q относительно середины ширины элемента b.
В случае
приложения к закладной детали кроме сдвигающей силы Q отрывающей силы N правая
часть условия (224) умножается на коэффициент ![]() , принимаемый не менее 0,2 (где Aout ¾ площадь проекции на плоскость,
перпендикулярную отрывающей силе N,
поверхности откалывания).
, принимаемый не менее 0,2 (где Aout ¾ площадь проекции на плоскость,
перпендикулярную отрывающей силе N,
поверхности откалывания).
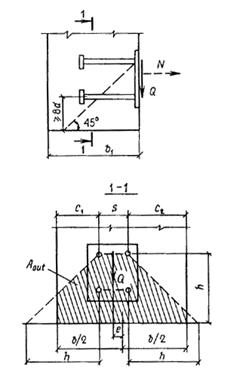
Черт. 76. Схема для расчета на откалывание бетона нормальными анкерами закладной детали
В случае приложения сдвигающей силы к закладной детали с наклонными анкерами, приваренными внахлестку и имеющими на концах усиления (см. п. 5.113), расчет на откалывание бетона производится в соответствии с Рекомендациями, упомянутыми в п. 3.102.
3.109. Если на концах анкеров закладной детали имеются усиления в виде анкерных пластинок или высаженных головок (см. п. 5.113), бетон под этими усилениями проверяется на смятие из условия
![]() , (225)
, (225)
где a, jb — коэффициенты определяемые согласно п. 3.93;
Аloc1 ¾ площадь анкерной пластины или сечения высаженной головки за вычетом площади сечения анкера;
Nloc — сила смятия, определяемая следующим образом:
а) для анкеров, приваренных втавр, при la ³ 15d:
если вдоль анкера возможно образование трещин от растяжения бетона или в случае применения гладких анкерных стержней ¾ по формуле
Nloc = Nan1; (226)
если образование этих трещин невозможно — по формуле
Nloc = Nan1 ![]() ; (227)
; (227)
б) для
анкеров, приваренных втавр, при la < 15d значение Nloc определенное по
формулам (226) и (227),
увеличивается на ![]() ;
;
в) для анкеров, приваренных внахлестку, Nloc определяется по формуле
nloc = Qinc. (228)
В формулах (226) ¾ (228):
Nan1, Qan1 ¾ соответственно наибольшее растягивающее и сдвигающее усилия, приходящиеся на один нормальный анкер (см. п. 3.101);
Qinc ¾ усилие в наклонном анкере.
Формулой (225) можно пользоваться, если толщина анкерной пластины составляет не менее 0,2 ее длины.
3.110. Определение перемещений сварных закладных деталей, расчет наклонных анкеров, приваренных под слоем флюса к пластине под углом более 45°, и расчет штампованных закладных деталей производятся согласно Рекомендациям, упомянутым в п. 3.102.
ПРИМЕРЫ РАСЧЕТА
Пример 50. Дано: закладная деталь колонны с приваренным столиком для опирания обвязочных балок, а также расположение и величины нагрузок от обвязочных балок — по черт. 77; анкера из арматуры класса А-III (Rs = 365 МПа); бетон колонны тяжелый класса В20; пластина из стали марки ВСт3кп2 (Ry = 215 МПа).
Требуется запроектировать нормальные анкера закладной детали и определить толщину пластины.
Черт. 77. К примеру расчета 50
Расчет. Принимаем расположение анкеров, как показано на черт. 77. Поскольку все нагрузки действуют в одном направлении и не вызывают кручения, определяем суммарную площадь поперечного сечения анкеров наиболее напряженного верхнего ряда по формуле (211).
Для этого вычислим момент внешних сил:
М = Ql = 150 × 0,15 = 22,5 кН×м.
Принимая z = 0,3м и N = 0, определим наибольшее растягивающее усилие в одном ряду анкеров по формуле (212):
![]()
На черт. 77 сдвигающая сила Q = 150 кН, число рядов анкеров nan = 3.
Сдвигающее усилие, приходящееся на один ряд анкеров, вычислим по формуле (213), принимая N¢an = Nan = 75 кН:
![]()
Коэффициент d определим по формуле (216).
Так как N¢an >
0, w = 0,3 ![]()
отсюда ![]()
Задаваясь диаметром анкеров 16 мм, по табл. 28 при классе бетона В20 и классе арматуры А-III находим l = 0,43, тогда
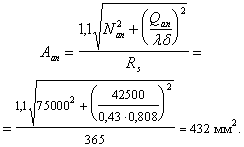
Принимаем по два анкера в каждом ряду диаметром 18 мм (Aan = 509 мм2).
Проверим значение Aan при коэффициенте, соответствующем принятому диаметру 18 мм, т. е. при l = 0,41:
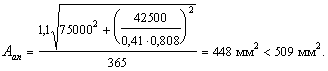
Оставляем 2Æ18.
Определим минимально допустимую длину анкеров без усилений lan согласно п. 5.112. Для этого вычислим коэффициент d3:
![]()
Значение Rb принимаем с учетом gb2 = 0,9 (нагрузки непродолжительного действия отсутствуют), т.е. Rb = 10,5 МПа.
Определим lan, предполагая „в запас" sbc < 0,25 Rb, т. е. принимая wan = 0,7, Dlan = 11:
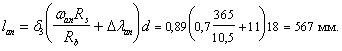
Учитывая, что площадь Aan принята с запасом, уточним значение lan:
![]()
Поскольку при такой длине анкеров размещение их в колонне невозможно, требуется уменьшить длину анкеров с устройством на концах усилений. Согласно п. 5.113, концы анкеров усиливаем высаженными головками диаметром dh = 54 мм ³ 3d и проверяем бетон на смятие под головкой и на выкалывание, приняв длину анкеров равной la = 250 мм > 10d = 10 × 18 = 180 мм.
Расчет на смятие производим согласно п. 3.109.
Площадь смятия Аloc1 под высаженной головкой одного анкера равна:
![]() .
.
Предположим "в запас", что в колонне со стороны закладной детали возможно образование трещин. Тогда, согласно п. 3.109, при la = 250 мм < 15 d = 15 × 18 = 270 мм сила смятия будет равна:
![]()
Принимаем максимальное значение jb = 2,5, поскольку расчетная площадь бетона Аloc2 здесь неопределенно велика; a = 1,0.
Проверим условие (225):
![]()
т. е. прочность на смятие обеспечена.
Поскольку N¢an > 0, расчет на выкалывание производим согласно п. 3.107. Концы анкеров с усилениями не заведены за продольную арматуру колонны, расположенную у противоположной от закладной детали грани колонны, поэтому расчет производим из условия (223).
Вычислим значение A1 (см. черт. 77):
A1
= (2 × 250 + 54) 400 ‑ 2 ![]() =
217000 мм2.
=
217000 мм2.
Усилие Nan = 75 кН приложено в центре тяжести площади А1, следовательно, е = 0. Для тяжелого бетона d1 = 0,5.
Проверим условие (223), пренебрегая ,,в запас" сжимающими напряжениями бетона (т. е. d2 = 1,0) и учитывая gb2 = 0,9 (т. е. Rbt = 0,8 МПа):
d1d2A1Rbt = 0,5 × 1 × 217000 × 0,80 = 86800 Н > Nan = 75000 Н,
т. е. прочность бетона на выкалывание обеспечена.
Принятые расстояния между анкерами в направлении поперек и вдоль сдвигающей силы, соответственно равные 260 мм > 5d = 5 × 18 = 90 мм и 150 мм > 7d = 7 × 18 = 126 мм, удовлетворяют требованиям п. 5.111. Расстояние от оси анкера до грани колонны, равное 70 мм > 3,5d = 3,5 × 18 = 63 мм, также удовлетворяет требованиям п. 5.111.
Конструкция
столика, приваренного к закладной детали, обеспечивает равномерное
распределение усилий между растянутыми анкерами и равномерную передачу
сжимающих напряжений на бетон, не вызывая изгиба пластины закладной детали.
Поэтому толщину этой пластины определим из условия (218), принимая Rsq
= 0,58 Ry = 0,58 ×
215 = 125 МПа, а диаметр анкера, требуемый по расчету, равным ![]() = 16,9
мм:
= 16,9
мм:
t = 0,25 ![]() =
0,25 ×
16,9
=
0,25 ×
16,9 ![]() = 12,3 мм.
= 12,3 мм.
Из условия механизированной дуговой сварки под флюсом (см. табл. 52, поз. 1) толщина пластины должна быть не менее 0,65d = 0,65 × 18 = 11,7 мм.
Принимаем толщину пластины t = 14 мм.
Пример 51. Дано: закладная деталь колонны с приваренным раскосом стальных связей — по черт. 78, а; растягивающая сила в раскосе от действия ветровых нагрузок 270 кН; анкера закладной детали из арматуры класса A-III (Rs = 365 МПа); пластина закладной детали из стали марки ВСт3сп2 (Ry = 215 МПа); бетон колонны тяжелый класса В30; армирование колонны — по черт. 78, б, минимальная продольная сила в колонне 1100 кН; изгибающий момент в колонне на уровне закладной детали в плоскости анкеров 40 кН × м.
Требуется запроектировать анкера закладной детали, определить толщину пластины и проверить прочность окружающего бетона на выкалывание.
Расчет. Принимаем расположение рядов анкеров по вертикали, как показано на черт. 78, в. Усилие в раскосе раскладываем на нормальную силу N, приложенную к закладной детали с эксцентриситетом e0 = 100 мм, и сдвигающую силу Q:
N = 270 cos 56°20¢ = 270 × 0,555 = 150 кН;
Q = 270 sin 56°20¢ = 270 × 0,832 = 225 кН.
При z = 0,42 м и M = Neo = 150 × 0,1 = 15 кН×м определим наибольшее растягивающее усилие в одном ряду анкеров по формуле (212):
![]()
Наибольшее сжимающее усилие в одном ряду анкеров вычислим по формуле (214):
![]()
т. е. прижатие пластины к бетону отсутствует.
Сдвигающее усилие Qan, приходящееся на один ряд анкеров, определим по формуле (213), принимая N¢an = 0:
![]() = 56,25 кН.
= 56,25 кН.
Так как N'an = 0,
w = 0,6 ![]() = 0,6
= 0,6![]() =
0 4,
=
0 4,
отсюда ![]() = 0,845 > 0,15.
= 0,845 > 0,15.
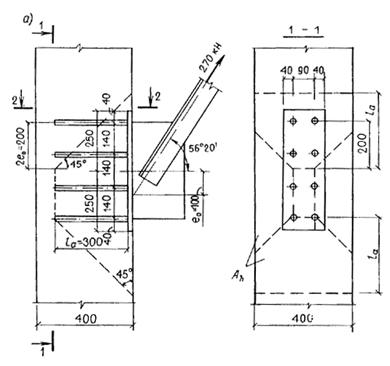
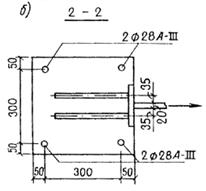
Черт. 78. К примеру расчета 51
По табл. 28, задаваясь диаметром анкеров 16 мм, при классе бетона В30 и анкерах из арматуры класса А-III находим l = 0,49, тогда
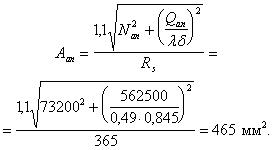
Принимаем по два анкера в каждом ряду диаметром 18 мм (Aan = 509 мм2). Проверим необходимое значение Aan при коэффициенте l, соответствующем принятому диаметру 18 мм, т. е. при l = 0,46:
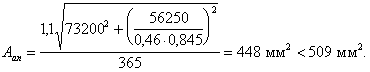
Оставляем по два анкера диаметром 18 мм. Располагаем анкера на минимальном расстоянии один от другого в горизонтальном направлении, равном 5d = 5 × 18 = 90 мм (см. п. 5.111). Расстояния между анкерами в вертикальном направлении (т. е. в направлении сдвигающей силы Q), равные 140 мм > 7d = 7 × 18 = 126 мм, также удовлетворяют требованию п. 5.111.
Определим толщину пластины закладной детали. Поскольку фасонка, передающая отрывающую силу на закладную деталь, располагается посредине расстояния между вертикальными рядами анкеров, толщину пластины определим из расчета на прочность пластины как консольной балки с вылетом 35 мм (см. черт. 78) на действие растягивающего усилия в одном анкере, равного:
![]() =
36,6 кН.
=
36,6 кН.
Ширину
консольной балки принимаем b = 80 мм. Расчет производим из условия М £ RyW,
где М = 36600 ×
35 = 1×280000 H×мм, ![]() ,
,
откуда 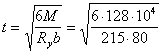 = 21,2
мм.
= 21,2
мм.
Принимаем пластину из полосовой стали толщиной 22 мм, при этом выполняются условие (218):
0,25 ![]() = 0,25
= 0,25
![]() = 12,6 мм < 22 мм и требования любого вида сварки
стержней втавр (см. табл. 52):
0,75d = 0,75 ×
18 = 13,5 мм < 22 мм.
= 12,6 мм < 22 мм и требования любого вида сварки
стержней втавр (см. табл. 52):
0,75d = 0,75 ×
18 = 13,5 мм < 22 мм.
Определим минимально допустимую длину анкеров без усилений по формуле (316) с учетом п. 5.112. Для этого вычислим коэффициент d3:
![]()
Значение Rb принимаем с учетом gb2 = 1,1, поскольку нагрузка на закладную деталь вызвана только ветровой нагрузкой, т. е. Rb = 19 МПа.
Для определения коэффициентов wan и Dl вычислим максимальное и минимальное напряжения бетона в пределах длины анкера. Для этого вычислим приведенные площадь Ared и момент инерции Ired сечения колонны, принимая по черт. 78, б Аs = А¢s = 1232 мм (2Æ28):
Аred = bh + 2Аs (a ‑ 1) = 400 × 400 + 2 × 1232 (6,9 ‑ 1) = 174,5 × 103 мм2;
Ired = ![]() + 2Аs (a ‑
1)(0,5h ‑ a)2 =
+ 2Аs (a ‑
1)(0,5h ‑ a)2 =
= ![]() + 2 × 1232 (6,9 ‑ 1) (0,5 × 400 ‑ 50)2 = 2460 × 106 мм4
+ 2 × 1232 (6,9 ‑ 1) (0,5 × 400 ‑ 50)2 = 2460 × 106 мм4
здесь ![]() = 6,9.
= 6,9.
Максимальное напряжение бетона в конце анкера длиной la = 300 мм (т. е. на расстоянии у = 300 + 22 400/2 = 122 мм от центра тяжести сечения):
![]() =
=
= 6,31 + 1,98 = 8,3 МПа < 0,75 Rb = 14,3 МПа.
Минимальное
напряжение бетона в начале анкера, т.
е. при у = ![]() ‑ 22 = 178 мм:
‑ 22 = 178 мм:
![]() =
=
= 3,42 МПа < 0,25 Rb = 4,75 МПа.
Поскольку анкер не расположен полностью в зоне с напряжением от 0,25Rb до 0,757Rb, определим длину части анкера а, расположенную в этой зоне:
![]()
Тогда, согласно формуле (317),
![]()
Dlan определяем аналогично wan с заменой коэффициентов 0,7 и 0,5 соответственно на 11 и 8 (см. табл. 44):
![]()
Допустимая длина анкера равна:
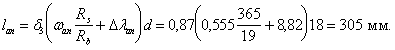
Учитывая, что
площадь Aan принята с запасом,
уточняем lan : lan = 305![]() = 292 мм.
= 292 мм.
Принимаем длину анкера la = 300 мм.
Проверим бетон на выкалывание.
Поскольку все анкера растянуты и не имеют усилений, расчет производим из условия (222). Определим площадь проекции поверхности выкалывания аh с учетом смещения наклонной грани на 2eo = 2 × 100 = 200 мм. При h = la = 300 мм
Ah = (420 ‑ 200 + 2 × 300) 400 = 32,8 × 104 мм2.
Так как сила N приложена в центре тяжести площади Ah, eh1 = еh2 = 0, d1 = 0,5 (как для тяжелого бетона).
По формуле (221) получим
d2 = 1 + 0,2
![]() = 1 + 0,2
= 1 + 0,2![]() = 1,145.
= 1,145.
Поскольку la = h, RsАап,а (la ‑ h)/lan = 0. Учитывая, что gb2 = 1,1, Rbt = 1,3 МПа.
d1d2AhRbt = 0,5 × 1,145 × 32,8 × 104 × 1,3 = 244300 Н > N = 150 кН.
Проверим условие (222) при h = 200 мм < la. Так как на расстоянии h от пластины поверхность выкалывания пересекает только две пары анкеров,
Aan1 = 1018 мм (4Æ18);
Аh = (420 ‑ 200 + 2 × 200) 400 = 24,2 × 104 мм2,
d1d2AhRbt + RsАап,а![]() =
=
= 0,5 × 1,145 × 24,2 × 104 × 1,3
+ 365 × 1018![]() =
=
= 304 × 103 Н > N = 150 кН.
Поскольку с уменьшением h несущая способность бетона на выкалывание повышается, расчет при меньших значениях h не производим.
Проверим условие (222) при значении h, равном высоте сечения колонны, т. е. h = 400 мм, без учета площади, расположенной между анкерами [(420 ‑ 200) 90 = 19800 мм2]:
Аh = (420 ‑ 200 + 2 × 400) 400 ‑ 19800 = 388 000 мм2 > 328000 мм2,
т. е. площадь Аh превышает площадь, вычисленную при h = 300 мм. Следовательно, прочность бетона на выкалывание обеспечена.
РАСЧЕТ СТЫКОВ СБОРНЫХ КОЛОНН
3.111. Стыки колонн, выполняемые ванной сваркой выпусков продольной арматуры, расположенных в специальных подрезках, при последующем замоноличивании этих подрезок (см. п. 5.90) рассчитываются для двух стадий работы:
1-я до замоноличивания стыка — на нагрузки, действующие на данном этапе возведения здания; при определении усилий такие стыки условно принимаются шарнирными;
2-я после замоноличивания стыка ¾ на нагрузки, действующие на данном этапе возведения здания и при эксплуатации; при определении усилий такие стыки принимаются жесткими.
3.112. Расчет незамоноличенных стыков колонн, указанных в п. 3.111 (черт. 79), производится на местное сжатие бетона колонны центрирующей прокладкой из условия (196) с добавлением в его правую часть усилия, воспринимаемого арматурными выпусками и равного:
Nout = 0,5 jRsc As (229)
где j ¾ коэффициент продольного изгиба для выпусков, определяемый в соответствии со СНиП II-23-81 (табл. 72) при расчетной длине lo, равной фактической длине свариваемых выпусков;
Аs ¾ площадь сечения всех выпусков.
При этом значение R*b,loc умножается на коэффициент yloc = 0,75, учитывающий неравномерность распределения нагрузки под центрирующей прокладкой, а за расчетную площадь Аloc2 принимается часть площади сечения торца колонны Aef в пределах контура сеток косвенного армирования размерами, не превышающими соответствующих утроенных размеров площади смятия Аloc1.
За площадь Аloc1 принимается площадь центрирующей прокладки или, если центрирующая прокладка приваривается при монтаже к распределительному листу (см. черт. 79), площадь этого листа. При этом его учитываемые размеры не должны превышать соответствующих размеров площади Aef, а толщина листа должна быть не менее 1/3 максимального расстояния от края листа до центрирующей прокладки.
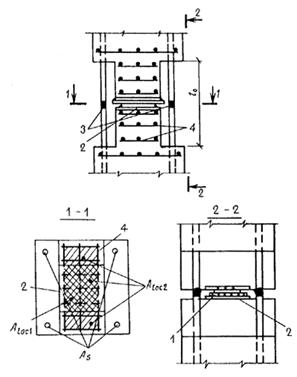
Черт. 79. Незамоноличенный стык колонны
1 ¾ центрирующая прокладка; 2 ¾ распределительный лист; 3 ¾ ванная сварка арматурных выпусков; 4 — сетки косвенного армирования торца колонны
3.113. Расчет замоноличенных стыков колонн, указанных в п. 3.111, производится как для сечения колонны на участке с подрезками согласно пп. 3.50¾3.76 с учетом следующих рекомендаций:
а) при наличии косвенного армирования сетками как в бетоне колонн, так и в бетоне замоноличивания расчет ведется согласно пп. 3.57 и 3.60, при этом рассматривается цельное сечение, ограниченное стержнями сеток, расположенными у граней замоноличенного участка колонны (черт. 80);
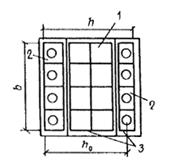
Черт. 80. Расчетное сечение замоноличенного стыка колонны с сетками косвенного армирования в бетоне колонны и в бетоне замоноличивания
1 ¾ бетон колонны; 2 ¾ бетон замоноличивания; 3 ¾ сетки косвенного армирования
б) при наличии косвенного армирования только в бетоне колонн расчет производится или с учетом этого косвенного армирования, но без учета бетона замоноличивания, или с учетом бетона замоноличивания, но без учета косвенного армирования колонн; прочность стыка считается обеспеченной при выполнении условия прочности хотя бы по одному из этих расчетов;
в) расчетные сопротивления бетона колонн и бетона замоноличивания (Rb или Rb,red) умножаются на коэффициенты условий работы, соответственно равные gbc = 0,9 и gbs = 0,8;
г) при расчете с учетом замоноличивания значение w определяется по формулам (15) или (104) по классу бетона замоноличивания, если он располагается по всей ширине наиболее сжатой грани, и по наибольшему классу бетона, если по сжатой грани располагается частично бетон замоноличивания и частично бетон колонны; в формуле (104) всегда учитывается минимальное значение mxy.
При расчете стыка с учетом бетона замоноличивания площадь сечения замоноличивания аbs рекомендуется приводить к площади сечения колонны умножением ее на отношение расчетных сопротивлений бетона замоноличивания и бетона колонны при неизменных высотах сечения замоноличивания.
Для симметрично армированных колонн прямоугольного сечения расчет замоноличенного стыка можно производить по формулам пп. 3.67 и 3.68, принимая за h¢f = hf высоту сечений подрезок, а за b¢f = bf ¾ ширину сечения, приведенного к бетону колонны, по наиболее сжатой стороне сечения.
Коэффициент h, учитывающий прогиб колонны (см. п. 3.54), определяется по геометрическим характеристикам сечения колонны вне зоны стыка.
3.114. Стыки колонн, выполняемые сопряжением торцов через слой цементного или полимерного раствора с обрывом продольной арматуры (см. п. 5.91, стыки 1-го и 2-го типов), в стадии эксплуатации рассчитываются как внецентренно сжатые бетонные элементы согласно п. 3.6 с учетом косвенного армирования сетками согласно пп. 3.57 и 3.60. При этом расчетное сопротивление бетона rb,red умножается на коэффициент условий работы gb, равный 0,9 или 1,0, при заполнении шва соответственно цементным или полимерным раствором. При отсутствии раствора между торцами колонн (например, в сферических стыках, в стыках с приторцованными поверхностями) указанный коэффициент условий работы принимается равным gb = 0,65.
ПРИМЕРЫ РАСЧЕТА
Пример 52. Дано: стык колонны - по черт. 81; бетон колонны класса В30 (Rbc = 15,5 МПа при gb2 = 0,9; Rb,ser = 22 МПа); бетон замоноличивания класса B20 (Rbs = 10,5 МПа при gb2 = 0,9; Rb,ser = 15 МПа); арматурные выпуски класса А-III (Rs = Rsc = 365 МПа; Rs,ser = 390 МПа), площадь их сечения Аs = А's = 4070 мм2 (4Æ36); сетки косвенного армирования их стержней класса А-III, диаметром 8 мм (Rs,xy = 355 МПа) с шагом s = 70 мм как в бетоне колонны, так и в бетоне замоноличивания; продольная сила в стадии эксплуатации N = 3900 кН при gf > 1,0 и N = 3300 кН при gf = 1,0, ее эксцентриситет в перпендикулярном подрезкам направлении с учетом прогиба колонны eo = 55 мм.
Требуется проверить прочность стыка в стадии эксплуатации и определить предельную продольную силу в стыке в стадии возведения здания.
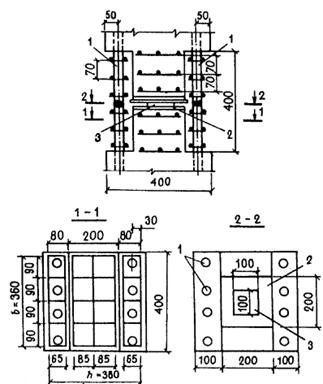
Черт. 81. К примеру расчета 52
1 ¾ арматурные выпуски; 2 — распределительный лист; 3 ¾ центрирующая прокладка
Расчет в стадии эксплуатации. В соответствии с п. 3.113a принимаем размеры сечения по осям крайних стержней сеток, т. е. b = h = 360 мм, ho = 330 мм (см. черт. 81).
Определим расчетное сопротивление бетона колонны и замоноличивания с учетом сеток косвенного армирования согласно п. 3.57.
Для бетона колонн:
Aef = 360 × 200 = 72 000 мм2 (см. черт. 81);
nx = 5; lx = 170 мм; пy = 3; ly = 360 мм; Asx = Asy = 50,3 мм2 (Æ8);
![]()
![]()
![]()
Отсюда значение Rbc,red с учетом коэффициента условий работы gbc = 0,9 (см. п. 3.113 в) равно:
Rbc,red = gbc (Rbc + jmхуRs,ху) =
= 0,9(15,5 + 2,0 × 0,0193 × 355) = 26,3 МПа.
Для бетона замоноличивания в одной из подрезок
Aef = 360 × 80 = 28 800 мм2 (см. черт. 81);
Asx = Asy = 50,3 мм2 (Æ8); lx = 65 мм; ly = 360 мм;
![]()
![]()
![]()
Значение Rbs,red с учетом коэффициента условий работы gbs = 0,8 равно:
Rbs,red = gbs (Rbs + jmхуRs,ху) =
= 0,8(10,5 + 1,47 × 0,026 × 355) = 19,3 МПа.
Определим значение w по формуле (104) по классу бетона замоноличивания, поскольку подрезка располагается по всей ширине наиболее сжатой грани колонны, при этом принимаем минимальное значение mxy = 0,0193:
d2 = 10mxy = 10 × 0,0193 = 0,19 > 0,15, принимаем d2 = 0,15;
w = 0,85 ‑ 0,008Rbs + d2 = 0,85 ‑ 0,008 × 10,5 + 0,15 = 0,916 > 0,9, принимаем w = 0,9.
Приводим сечение стыка к бетону колонны, при этом ширина подрезки становится равной:
![]() = 264 мм;
= 264 мм;
высота подрезки h¢f = 80 мм (см. черт. 81).
Прочность стыка проверим согласно п. 3.67.
Для этого по формуле (14) определим значение xR принимая ssc,и = 500 МПа:
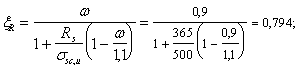
Aov = (b'f ‑ b) h¢f = (264 ‑ 360)80 = ‑ 7680 мм2.
Высота сжатой зоны равна:
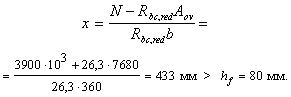
Так как х = 433 мм > xR ho = 0,794 × 330 = 260 мм, высоту сжатой зоны определим по формуле (132).
Для этого вычислим:
![]()
![]()
![]()
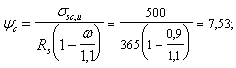
![]()
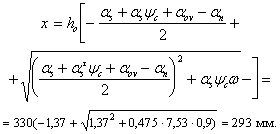
Значение е равно e
= eo + ![]() = 55 +
= 55 + ![]() = 205
мм.
= 205
мм.
Прочность стыка проверим по условию (131):
Rbc,redbx (ho ‑ x/2) + Rbc,redAov (ho ‑ h¢f/2) + Rsc A¢s (ho ‑ a¢) =
= 26,3 × 360 × 293 (330 ‑ 293/2) ‑ 26,3 × 7680 (330 ‑ 80/2) +
+ 365 × 4070 (330 ‑ 30) = 896,1 × 106 H × мм > Ne = 3900 × 0,205 = 800 кН × м,
т. е. прочность стыка в стадии эксплуатации обеспечена.
Проверим трещиностойкость защитного слоя замоноличенного участка колонны согласно п. 3.60 по аналогии с расчетом по прочности стыка в стадии эксплуатации:
ho = h ‑ a = 400 ‑ 50 = 350 мм;
w = 0,85 ‑ 0,006Rbs,ser = 0,85 ‑ 0,006 × 15 = 0,76;
![]() = 273 мм; h¢f = 100 мм;
= 273 мм; h¢f = 100 мм;
Aov = (b'f ‑ b) h¢f = (273 ‑ 400) 100 = ‑12700 мм2;
Rs = Rsc = Rs,ser = 390 МПа;
![]()
![]()
![]()
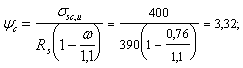
![]()
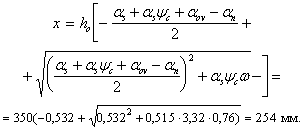
e = eo
+ ![]() = 55 +
= 55 + ![]() = 205
мм;
= 205
мм;
Rbc,serbx (ho ‑ x/2) + Rbc,serAov (ho ‑ h¢f/2) + RscA¢s (ho ‑ a¢) =
= 22 × 400 × 254 (350 ‑ 254/2) ‑ 22 × 12700 (350 ‑ 100/2) + 390 × 4070 (350 ‑ 50) =
= 890,8 × 106 H×мм > Ne = 3300 × 0,205 = 677 кН×м.
Расчет незамоноличенного стыка в стадии возведения. Определяем расчетное сопротивление бетона смятию с учетом косвенного армирования согласно пп. 3.93 и 3.112.
Площадь части сечения торца колонны, ограниченная контуром сеток, равна:
Aef = 170 × 360 = 61200 мм2.
За площадь смятия принимаем площадь распределительного листа, поскольку его толщина 20 мм превышает 1/3 расстояния от края листа до центрирующей прокладки (50 × 1/3 = 17 мм), при этом ширину площади смятия принимаем равной ширине сетки — 170 мм.
Aloc1 = 200 × 170 = 34 000 мм2.
Поскольку 360 мм < 3 × 200 мм, принимаем Aloc2 = Aef = 61200 мм2,
отсюда 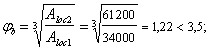
![]()
![]()
Поскольку расчет производим на нагрузки в стадии возведения, принимаем Rbc = 19 МПа (т. e. при gи2 = 1,1):
![]()
![]()
Значение R*b,loc определяем по формуле (197), учитывая коэффициент yloc = 0,75:
R*b,loc = yloc (Rb jb + jmxy Rs,xy js) = 0,75 (19 × 1,22 +
+ 1,97 × 0,0226 × 355 ×2,56) = 47,7 МПа.
По формуле (229) определим усилие в арматурных выпусках.
Радиус инерции арматурного стержня Æ36 равен:
![]() =
9 мм.
=
9 мм.
Длина сваренных выпусков l = lo = 400 мм.
Согласно табл.
72 СНиП II-23-81 при l = ![]() =
= ![]() =
44,4 и Ry = Rs = 365 МПа находим j = 0,838, отсюда Nout
= 0,5 jRsАs = 0,5 × 0,838 ´ 365 × 8140 = 1245 × 103 H.
=
44,4 и Ry = Rs = 365 МПа находим j = 0,838, отсюда Nout
= 0,5 jRsАs = 0,5 × 0,838 ´ 365 × 8140 = 1245 × 103 H.
Предельная продольная сила, воспринимаемая незамоноличенным стыком, равна:
N = R*b,loc Aloc1 + Nоut = 47,7 × 34000 + 1245 × 103 = 2867 × 103 H.
РАСЧЕТ БЕТОННЫХ ШПОНОК
3.115. Размеры бетонных шпонок, передающих сдвигающие усилия между сборным элементом и дополнительно уложенным бетоном или раствором (черт. 82), рекомендуется определять по формулам :
![]() (230)
(230)
![]() (231)
(231)
где Q — сдвигающая сила, передающаяся через шпонки;
tk, hk, lk ¾ глубина, высота и длина шпонки;
пk — число шпонок, вводимое в расчет и принимаемое не более трех.
Черт. 82. Схема для расчета шпонок, передающих сдвигающие усилия от сборного элемента монолитному бетону
1 ¾ сборный элемент; 2 ¾ монолитный бетон
При наличии сжимающей силы N высоту шпонок допускается определять по формуле
![]() (231)
(231)
и принимать уменьшенной по сравнению с высотой, определяемой по формуле (231), не более чем в 2 раза.
При соединении шпонками элементов настила длина шпонки, вводимая в расчет, должна составлять не более половины пролета элемента, при этом величина Q принимается равной сумме сдвигающих усилий по всей длине элемента.
По условиям (230) ¾ (232) следует проверять шпонки сборного элемента и шпонки из дополнительно уложенного бетона, принимая расчетные сопротивления бетона шпонок Rb и Rbt как для бетонных конструкций.
Примечание. При расчете на выдергивание растянутой ветви двухветвевой колонны из стакана фундамента допускается учитывать работу пяти шпонок.
4. РАСЧЕТ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ОБРАЗОВАНИЮ ТРЕЩИН
4.1(4.1). Железобетонные элементы рассчитываются по образованию трещин:
нормальных к продольной оси элемента;
наклонных к продольной оси элемента.
Расчет по образованию трещин производится:
а) для выявления необходимости проверки по раскрытию трещин;
б) для выяснения случая расчета по деформациям.
В железобетонном элементе или на его участках трещины отсутствуют, если усилия, вызванные действием полной нагрузки (или ее части, когда нагрузки вызывают усилия разных знаков) и вводимые в расчёт с коэффициентом надежности по нагрузке gf = 1,0, меньше усилий, воспринимаемых сечением при образовании трещин. Полная нагрузка включает постоянные, длительные и кратковременные нагрузки.
Допускается принимать без расчета, что изгибаемые элементы сечений прямоугольного и таврового со сжатыми полками имеют на наиболее напряженных участках трещины, нормальные к продольной оси, если требуемый по расчету коэффициент армирования m > 0,005.
4.2(4.5). Расчет железобетонных элементов по образованию нормальных трещин производится из условия
Мr < Мcrc, (233)
где Мr ¾ момент внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется;
Мcrc — момент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин, и определяемый по формуле
Mcrc = Rbt,serWpl ![]() Mshr, (234)
Mshr, (234)
здесь Mshr ¾ момент усилия Nshr вызванного усадкой бетона, относительно той же оси, что и для определения Мr; знак момента определяется направлениями вращения ("плюс" ¾ когда направления противоположны, "минус" ¾ когда направления моментов Мshr и Мr совпадают).
Для свободно опертых балок и плит момент Мcrc определяется по формуле
Mcrc = Rbt,serWpl ‑ Nshr (eop + r). (235)
Усилие Nshr рассматривается как внешняя растягивающая сила; его величина и эксцентриситет относительно центра тяжести приведенного сечения определяются по формулам:
Nshr = sshr (As + A¢s); (236)
![]() , (237)
, (237)
где sshr ¾ напряжение в арматуре, вызванное усадкой бетона, равное: для тяжелого бетона класса В35 и ниже — 40 МПа при естественном твердении и 35 МПа ¾ при тепловой обработке; для других видов и классов бетона sshr принимается согласно СНиП 2.03.01-84 (табл. 5, поз. 8);
уs, у¢s ¾ расстояния от центра тяжести приведенного сечения до центров тяжести сечений соответственно арматуры S и S¢.
Если коэффициент армирования m < 0,01, допускается в формулах (234) и (235) величины Wpl и r определять как для бетонного сечения, принимая Nshr = 0 и As = A's = 0.
Значение Mr определяется по формулам:
для изгибаемых элементов (черт. 83, а)
Мr = М;
для внецентренно сжатых элементов (черт. 83, б)
Mr = N(eo ‑ r), (238)
для центрально- и внецентренно растянутых элементов (черт. 83, в)
Mr = N(eo + r), (239)
В формулах (234), (235), (238) и (239):
r — расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
Значение r определяется для элементов:
изгибаемых — по формуле
![]() ;
(240)
;
(240)
внецентренно сжатых — по формуле
![]() (241)
(241)
здесь ![]()
но принимается не менее 0,7 и не более 1,0;
sb — максимальное напряжение в сжатом бетоне, вычисляемое как для упругого тела по приведенному сечению;
центрально- и внецентренно растянутых — по формуле
![]() , (242)
, (242)
Wpl ¾ момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый согласно п.4.3.
Примечание. Приведенное сечение включает сечение бетона, а также сечение всей продольной арматуры, умноженное на отношение соответствующих модулей упругости арматуры и бетона.
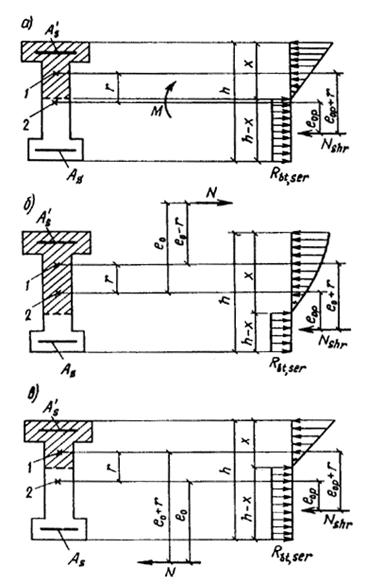
Черт. 83. Схемы усилий и эпюры напряжений в поперечном сечении элемента при расчете его по образованию трещин, нормальных к продольной оси элемента
а ¾ при изгибе; б ¾ при внецентренном сжатии; в ¾ при центральном и внецентренном растяжении; 1 ¾ ядровая точка; 2 ¾ центр тяжести приведенного сечения
4.3 (4.7). Момент сопротивления приведенного сечения для крайнего растянутого волокна Wpl (с учетом неупругих деформаций растянутого бетона) определяется в предположении отсутствия продольной силы N по формуле
![]() , (243)
, (243)
где Ibo, Iso, I¢so — моменты инерции соответственно площадей сечения сжатой зоны бетона, арматуры S и S¢ относительно нулевой линии;
Sbo — статический момент площади сечения растянутой зоны бетона относительно нулевой линии.
Положение нулевой линии в общем случае определяется из условия
![]() , (244)
, (244)
где S¢bo, Sso, S¢so ¾ статические моменты соответственно площади сечения сжатой зоны бетона, арматуры S и S¢ относительно нулевой линии;
Abt — площадь сечения растянутой зоны бетона.
Для прямоугольных, тавровых и двутавровых сечений условие (244) принимает вид
![]() (245)
(245)
где ![]() ¾ статический момент
площади приведенного сечения, вычисленный без учета площади бетона растянутых
свесов, относительно крайнего растянутого волокна;
¾ статический момент
площади приведенного сечения, вычисленный без учета площади бетона растянутых
свесов, относительно крайнего растянутого волокна;
![]() ¾
площадь приведенного сечения, вычисленная без учета половины площади бетона
растянутых свесов.
¾
площадь приведенного сечения, вычисленная без учета половины площади бетона
растянутых свесов.
Условием (245) можно пользоваться, если найденная по нему нулевая линия пересекает ребро таврового или двутаврового сечения.
Значение Wpl допускается определять по формуле
Wpl = [0,292 + 0,75 (g1 + 2m1a) + 0,075(g¢1 + 2m¢1a)] bh2; (246)
где ![]()
![]()
При известном значении Wred (см. п. 4.2) величину Wpl можно также определить по формуле
Wpl = g Wred, (247)
где g ¾ см. табл. 29.
Таблица 29
|
Сечение |
Коэффициент g |
Форма поперечного сечения |
|
1. Прямоугольное |
1,75 |
|
|
2. Тавровое с полкой, расположенной в сжатой зоне |
1,75 |
|
|
3. Тавровое с полкой (уширением), расположенной, в растянутой зоне: а) при bf/b £ 2 независимо от отношения hf/h б) bf/b > 2 и hf/h > 0,2 в) bf/b > 2 и hf/h < 0,2 |
1,75
1,75 1,50 |
|
|
4. Двутавровое симметричное (коробчатое): а) при b¢f/b = bf/b £ 2 независимо от отношений h¢f/h = hf/h б) при 2 < b¢f/b = bf/b £ 6 независимо от отношений h¢f/h = hf/h в) при b'f/b = b¢f/b > 6 и h¢f/h = h¢f/h > 0,2 г) при 6 < b¢f/b = bf/b £ 15 и h¢f/h = hf/h < 0,2 д) при b¢f/b = bf/b > 15 и h¢f/h = hf/h < 0,2 |
1,75
1,50
1,50
1,25
1,10 |
|
|
5. Двутавровое несимметричное, удовлетворяющее условию b¢f/b < 3: а) при bf/b £ 2 независимо от отношения hf/h б) при2 < bf/b £ 6 независимо от отношения hf/h в) при bf/b > 6 и hf/h > 0,1 |
1,75
1,50
1,50 |
|
|
6. Двутавровое несимметричное, удовлетворяющее условию 3 < b¢f/b £ 8: а) при b¢f/b £ 4 независимо от отношения hf/h б) при bf/b > 4 и hf/h ³ 0,2 в) при bf/b > 4 и hf/h < 0,2 |
1,50
1,50
1,25 |
|
|
7. Двутавровое несимметричное, удовлетворяющее условию b¢f/b ³ 8: а) при hf/h > 0,3 б) при hf/h < 0,3 |
1,50 1,25 |
|
|
8. Кольцевое и круглое |
2-0,4D1/D |
|
|
9. Крестовое: а) при b¢f/b ³ 2 и 0,9 ³ h¢f/h > 0,2 б) в остальных случаях |
2,00
1,75 |
|
Примечания: 1. В табл. 29 обозначения bf и hf соответствуют размерам полки, которая при расчете по образованию трещин растянута, a b¢f и h¢f — размерам полки, которая для этого случая расчета сжата.
2. Wpl = g Wred, где Wred ¾ момент сопротивления для растянутой грани приведенного сечения, определяемый по правилам сопротивления упругих материалов.
4.4. Участки по длине элемента, на которых отсутствуют наклонные трещины, определяются из условия
Q £ jb3 Rbt.serbho, (248)
где jb3 — см. табл. 21.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН
(4.13). Железобетонные элементы рассчитываются по раскрытию трещин:
нормальных к продольной оси элемента;
наклонных к продольной оси элемента.
Проверка ширины раскрытия трещин не требуется, если, согласно расчету по пп. 4.1¾4.4, они не образуются от действия постоянных, длительных и кратковременных нагрузок, вводимых в расчет с коэффициентом надежности по нагрузке gf = 1,0.
Для изгибаемых и внецентренно сжатых элементов статически определимых систем при однорядном армировании, указанных в табл. 1, поз. 4, проверка ширины раскрытия нормальных трещин не требуется в следующих случаях:
а) для арматуры классов А-I и А-II:
при любых коэффициентах армирования m, если диаметр d £ 20 мм;
при m ³ 0,01, если диаметр d = 22 ¾ 40 мм;
б) для арматуры класса А-III:
при любых коэффициентах армирования m, если диаметр d £ 8 мм;
при m ³ 0,01, если диаметр d = 10 — 25 мм;
при m ³ 0,015, если диаметр d = 28 ¾ 40 мм;
в) для арматуры класса Вр-1 ¾ при m ³ 0,006 при любых диаметрах.
При расчете по ракрытию трещин усилие от усадки бетона Nshr принимается равным нулю.
4.6. В общем случае расчет по раскрытию трещин производится два раза: на непродолжительное и продолжительное раскрытие трещин (см. п. 1.15).
Для элементов, указанных в табл. 1, поз. 4 и выполняемых из тяжелого и легкого бетонов, при проверке раскрытия трещин, нормальных к продольной оси элемента, допускается расчет производить только один раз:
если ![]() , проверяется продолжительное раскрытие трещин;
, проверяется продолжительное раскрытие трещин;
если ![]() , проверяется непродолжительное раскрытие трещин,
, проверяется непродолжительное раскрытие трещин,
здесь Mrl, Mr — момент Mr (см. п. 4.2) соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.
Расчет по раскрытию трещин, нормальных к продольной оси элемента
4.7(4.14). Ширину раскрытия трещин, нормальных к продольной оси элемента, acrc, мм, следует определять по формуле
![]() (249)
(249)
где d ¾ коэффициент, принимаемый равным для элементов:
изгибаемых и внецентренно сжат......... 1,0
растянутых ............................................ 1,2
jl — коэффициент, принимаемый равным при учете:
кратковременных нагрузок и непродолжительного
действия постоянных и длительных нагрузок............... 1,00
продолжительного действия постоянных и
длительных нагрузок для конструкций из бетона:
тяжелого:
естественной
влажности......................![]()
в водонасыщенном состоянии (элементы, воспринимающие давление жидкостей, а также эксплуатируемые в грунте ниже уровня грунтовых вод) ............................................. 1,20
при попеременном водонасыщении и высушивании 1,75
мелкозернистого групп:
А .......................................................................... 1,75
Б ........................................................................... 2,00
В ........................................................................... 1,50
легкого класса В12,5 и выше .................................... 1,50
поризованного ........................................................... 2,00
значения jl для мелкозернистого, легкого и поризованного бетонов в водонасыщенном состоянии умножаются на коэффициент 0,8, а при попеременном водонасыщении и высушивании ¾ на коэффициент 1,2;
h — коэффициент, принимаемый равным для арматуры классов: А-II и А-III ¾ 1,0; А-I — 1,3; Вр-1 ¾ 1,2;
ss ¾ напряжение в стержнях крайнего ряда арматуры S, определяемое согласно п. 4.9;
![]() ¾
коэффициент армирования сечения, принимаемый равным отношению площади сечения
арматуры S к площади сечения бетона
(при рабочей высоте ho и без учета сжатых
свесов полок), но не более 0,02, при этом для двутавровых, прямоугольных и
тавровых сечений
¾
коэффициент армирования сечения, принимаемый равным отношению площади сечения
арматуры S к площади сечения бетона
(при рабочей высоте ho и без учета сжатых
свесов полок), но не более 0,02, при этом для двутавровых, прямоугольных и
тавровых сечений
![]() (250)
(250)
если hf < а, растянутые свесы при вычислении ![]() не учитываются;
не учитываются;
если во внецентренно растянутых элементах сила N расположена между центрами тяжести арматуры S и S¢, при определении ![]() рабочая высота ho принимается от точки приложения силы N
до менее растянутой грани, при этом для центрального растяжения
рабочая высота ho принимается от точки приложения силы N
до менее растянутой грани, при этом для центрального растяжения ![]() , где As,tot — площадь всей продольной арматуры;
, где As,tot — площадь всей продольной арматуры;
d — диаметр растянутой арматуры, мм; при различных диаметрах стержней значение d принимается равным:
![]() (251)
(251)
здесь d1, ..., dk ¾ диаметр стержней растянутой арматуры;
п1, ..., nk ¾ число стержней диаметрами соответственно d1, ..., dk. Кроме того, следует учитывать указания п. 4.8.
4.8 (4.14). Ширина раскрытия трещин асrc, определенная согласно п. 4.7, корректируется в следующих случаях:
а) если центр тяжести сечения стержней крайнего ряда арматуры S изгибаемых, внецентренно сжатых, внецентренно растянутых при eо ³ 0,8ho элементов отстоит от наиболее растянутого волокна бетона на расстоянии a2 > 0,2h, значение acrc должно быть увеличено умножением на коэффициент da, равный:
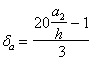 (252)
(252)
и принимаемый не более 3;
б) для
слабоармированных изгибаемых и внецентренно сжатых элементов из тяжелого и
легкого бетонов (например, фундаментов) при ![]() (
(![]() ¾ см. п. 4.7) величину асrc,
вычисленную по формуле (249), при необходимости допускается уменьшать
умножением на коэффициент jb, учитывающий работу растянутого бетона
над трещинами и определяемый по формуле
¾ см. п. 4.7) величину асrc,
вычисленную по формуле (249), при необходимости допускается уменьшать
умножением на коэффициент jb, учитывающий работу растянутого бетона
над трещинами и определяемый по формуле
jb = jf1 jl1, (253)
но не более 1,0,
где jf1 — коэффициент, учитывающий уровень нагружения и равный:
![]() (254)
(254)
jl1 — коэффициент, учитывающий длительность действия нагрузки и равный при учете:
кратковременных нагрузок и непродолжительного действия постоянных и длительных нагрузок 1,0;
продолжительного действия постоянных и длительных нагрузок
![]() (255)
(255)
но не менее 1,0;
Мo ¾ момент, при котором растянутый бетон над трещинами практически выключается из работы, равный:
Мо = Мсгс + ybh2Rbt,ser, (256)
где ![]() , но не более 0,6;
, но не более 0,6;
если Mо < Mr, коэффициент jb не вычисляется;
Mr ¾ момент, определяемый, согласно п. 4.2, от полной нагрузки, включающ ей постоянную, длительную и кратковременную нагрузки;
Mcrc ¾ см. п. 4.2;
![]() ¾
см. п. 4.7.
¾
см. п. 4.7.
При
использовании коэффициента jb
и при ![]() не следует
пользоваться рекомендациями п. 4.6;
не следует
пользоваться рекомендациями п. 4.6;
в) для статически неопределимых систем, а также для свободно опертых балок при l/h < 7, вблизи мест приложения сосредоточенных сил и опорных реакций при m < 0,02 ширину раскрытия трещин acrc, вычисленную по формуле (249), допускается уменьшать умножением на коэффициент jloc, учитывающий местные особенности напряженного состояния в железобетонных конструкциях и определяемый по формуле
![]() , (257)
, (257)
но не менее 0,8 и не более 1,0,
где F — абсолютное значение сосредоточенной силы или опорной реакции;
М — абсолютное значение изгибающего момента в нормальном сечении, проходящем через точку приложения сосредоточенной силы или опорной реакции (черт. 84);
а — расстояние от точки приложения сосредоточенной силы или опорной реакции до рассматриваемого сечения, принимаемое в соответствии с черт. 84, но не более 0,3h;
h — расстояние от грани элемента, к которой приложена сила F, до растянутой грани;
ho — то же, до растянутой арматуры (черт. 85);
г) для элементов из легкого бетона класса В7,5 и ниже величина acrc должна быть увеличена на 20 %.
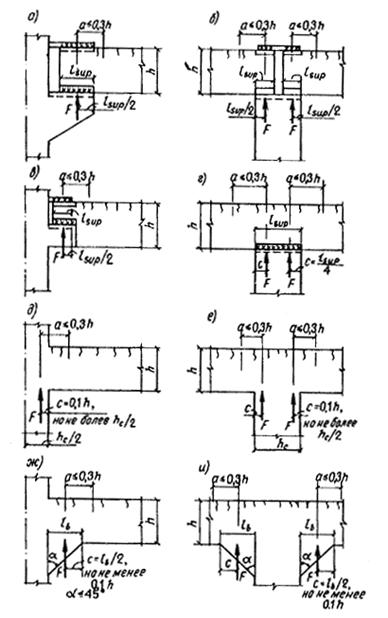
Черт. 84. Положение опорных реакций в жестких узлах, принимаемое для определения коэффициента jloc
а - г ¾ стыки сборных элементов; д - и ¾ монолитные сопряжения
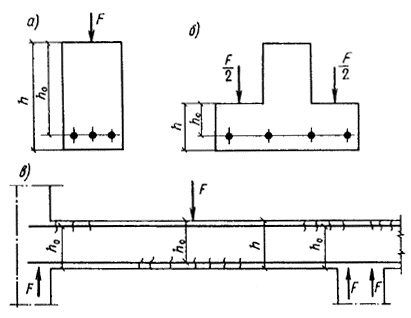
Черт. 85. Расчетные схемы для определения коэффициента jloc
а ¾ при приложении силы к сжатой грани элемента; б ¾ то же, к уширениям (полкам) элемента; в ¾ то же, по длине статически неопределимой балки
(4.15). Напряжения в растянутой арматуре ss (определяются по формулам для элементов:
центрально-растянутых
![]() (258)
(258)
изгибаемых
![]() ; (259)
; (259)
внецентренно сжатых и внецентренно растянутых
![]() . (260)
. (260)
В формуле (260) знак «плюс» принимается при внецентренном растяжении, знак «минус» ¾ при внецентренном сжатии. При расположении растягивающей продольной силы N между центрами тяжести арматуры S и S¢ значение еs принимается со знаком «минус».
В формулах (259) и (260) :
z —
расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения
над трещиной, определяемое согласно п. 4.16, при этом для внецентренно
растянутых элементов при ео
< 0,8ho z принимается равным zs — расстоянию между центрами тяжести арматуры S и S¢,
коэффициент v в формуле (277) принимается всегда
равным vsh = 0,45 (как при
непродолжительном действии нагрузки); допускается z принимать таким же, как при расчете по деформациям на те же нагрузки, если ![]()
В случае, когда Mr < Mcrc (см. п. 4.2), значение ss, определяется по формуле
![]() (261)
(261)
где ss,crc ¾ напряжение в арматуре при действии нагрузки, соответствующей образованию трещин, определяемое по формулам (259) и (260) с заменой М на
Mcrc и N на ![]()
При определении Ncrc моменты Mcrc и Mr допускается вычислять при r = 0,8Wred/Ared.
При расположении растянутой арматуры в несколько рядов по высоте сечения в изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементах при eo > 0,8ho напряжения ss необходимо умножать на коэффициент dn, равный:
![]() (262)
(262)
где х = xho; значение x определяется по формуле (274); для изгибаемых элементов допускается принимать значение х таким же, как и при расчете по прочности;
а1, a2 — расстояния от центра тяжести площади сечения соответственно всей арматуры S и крайнего ряда стержней до наиболее растянутого волокна бетона.
Значение напряжения ss от действия полной нагрузки, определенное с учетом коэффициента dn, не должно превышать Rs,ser. Это условие допускается не проверять для статически определимых конструкций с арматурой одного класса при ее однорядном расположении.
Упрощенные способы определения ss. Для изгибаемых элементов допускается определять ss по формуле
![]() (263)
(263)
где Ми — предельный момент по прочности, равный:
при проверке прочности сечений ¾ правой части неравенств (17) — (21), (28), (30)
при подборе сечения арматуры
![]()
здесь Mtot,d — момент от действия полной нагрузки с коэффициентом надежности по нагрузке gf > 1,0;
Аs,fact — фактическая площадь принятой арматуры;
Asd — площадь арматуры, требуемая по расчету прочности.
При применении арматуры разных классов в формулу (263) вводится расчетное сопротивление арматуры для предельных состояний первой группы Rs по более прочной арматуре.
Для внецентренно сжатых элементов из тяжелого и легкого бетонов при Mr ³ Mcrc допускается вычислять ss по формуле
![]() 4)
4)
где jcrc — коэффициент, определяемый по табл. 30.
Таблица 30
|
jf |
|
Коэффициенты jcrc при значениях ma, равных |
|||||||||||
|
|
|
0,01 |
0,02 |
0,03 |
0,05 |
0,07 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,40 |
0,50 |
|
0 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,18 0,31 0,44 0,59 0,74 0,81 |
0,07 0,22 0,34 0,48 0,62 0,77 0,84 |
0,10 0,25 0,37 0,50 0,64 0,79 0,86 |
0,15 0,29 0,40 0,53 0,67 0,82 0,89 |
0,18 0,31 0,43 0,56 0,70 0,84 0,91 |
0,22 0,34 0,46 0,58 0,72 0,86 0,94 |
0,26 0,38 0,49 0,62 0,75 0,89 0,97 |
0,31 0,42 0,55 0,65 0,78 0,92 1,00 |
0,34 0,45 0,55 0,67 0,81 0,95 1,02 |
0,37 0,47 0,57 0,69 0,82 0,96 1,03 |
0,41 0,50 0,60 0,72 0,85 0,99 1,06 |
0,45 0,52 0,62 0,74 0,87 1,01 1,08 |
|
0,05 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,17 0,30 0,44 0,59 0,74 0,82 |
0,04 0,20 0,33 0,46 0,61 0,76 0,84 |
0,07 0,22 0,35 0,48 0,63 0,78 0,85 |
0,11 0,26 0,38 0,51 0,65 0,80 0,86 |
0,14 0,28 0,40 0,53 0,67 0,82 0,90 |
0,18 0,31 0,43 0,56 0,70 0,84 0,92 |
0,22 0,34 0,46 0,59 0,72 0,87 0,94 |
0,26 0,38 0,49 0,61 0,75 0,89 0,97 |
0,29 0,40 0,51 0,64 0,77 0,91 0,99 |
0,32 0,42 0,53 0,66 0,79 0,93 1,00 |
0,36 0,46 0,56 0,68 0,82 0,95 1,03 |
0,38 0,48 0,58 0,70 0,83 0,97 1,04 |
|
0,10 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,03 0,16 0,30 0,44 0,59 0,75 0,83 |
0,04 0,19 0,32 0,46 0,61 0,76 0,84 |
0,05 0,21 0,33 0,47 0,62 0,77 0,85 |
0,09 0,24 0,36 0,50 0,64 0,79 0,87 |
0,11 0,26 0,38 0,52 0,66 0,81 0,88 |
0,14 0,28 0,40 0,54 0,68 0,83 0,90 |
0,16 0,31 0,43 0,56 0,70 0,85 0,92 |
0,22 0,34 0,46 0,59 0,73 0,87 0,94 |
0,25 0,37 0,48 0,61 0,75 0,89 0,96 |
0,28 0,39 0,50 0,63 0,76 0,90 0,98 |
0,31 0,42 0,53 0,65 0,79 0,93 1,00 |
0,34 0,44 0,55 0,67 0,80 0,94 1,02 |
|
0,20 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,03 0,15 0,29 0,44 0,59 0,75 0,83 |
0,04 0,17 0,31 0,45 0,60 0,76 0,84 |
0,05 0,19 0,32 0,46 0,61 0,77 0,85 |
0,06 0,21 0,34 0,48 0,63 0,78 0,86 |
0,07 0,23 0,35 0,49 0,64 0,79 0,87 |
0,10 0,25 0,37 0,51 0,65 0,81 0,88 |
0,13 0,27 0,40 0,53 0,67 0,82 0,90 |
0,16 0,30 0,42 0,55 0,69 0,84 0,91 |
0,19 0,32 0,44 0.57 0,71 0,85 0,93 |
0,21 0,34 0,45 058 0,72 0,87 0,94 |
0,25 0,37 0,48 0,61 0,75 0,89 0,96 |
0,28 0,39 0,50 0,63 0,76 0,90 0.98 |
|
0,30 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,03 0,15 0,29 0,44 0,59 0,75 0,84 |
0,04 0,16 0,30 0,45 0,60 0,76 0,85 |
0,05 0,17 0,31 0,46 0,61 0,77 0,85 |
0,05 0,19 0,33 0,47 0,62 0,78 0,86 |
0,06 0,21 0,34 0,48 0,63 0,78 0,86 |
0,07 0,23 0,35 0,49 0,64 0,79 0,87 |
0,10 0,25 0,37 0,51 0,66 0,81 0,89 |
0,12 0,27 0,39 0,53 0,67 0,82 0,90 |
0,15 0,29 0,41 0,54 0,68 0,83 0,91 |
0,17 0,30 0,42 0,55 0,70 0,84 0,92 |
0,20 0,33 0,45 0,58 0,72 0,86 0,94 |
0,23 0,35 0,46 0,59 0,73 0,88 0,95 |
|
0,50 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,15 0,29 0,44 0,60 0,77 0,85 |
0,04 0,16 0,30 0,45 0,61 0,77 0,85 |
0,04 0,16 0,30 0,45 0,61 0,77 0,85 |
0,04 0,18 0,31 0,46 0,62 0,77 0,86 |
0,04 0,19 0,32 0,47 0,62 0,78 0,86 |
0,04 0,20 0,33 0,48 0,63 0,79 0,87 |
0,06 0,22 0,35 0,49 0,64 0,79 0,87 |
0,08 0,23 0,36 0,50 0,65 0,80 0,88 |
0,10 0,24 0,37 0,51 0,66 0,81 0,89 |
0,12 0,26 0,38 0,52 0,67 0,82 0,89 |
0,15 0,28 0,40 0,54 0,68 0,83 0,91 |
0,17 0,30 0,42 0,55 0,69 0,84 0,92 |
|
0,70 |
£0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,15 0,29 0,45 0,61 0,77 0,85 |
0,04 0,15 0,30 0,45 0,61 0,77 0,85 |
0,04 0,16 0,30 0,45 0,61 0,77 0,85 |
0,04 0,17 0,31 0,46 0,61 0,77 0,86 |
0,04 0,18 0,32 0,46 0,62 0,78 0,86 |
0,04 0,19 0,32 0,47 0,62 0,78 0,86 |
0,04 0,20 0,34 0,48 0,63 0,79 0,87 |
0,06 0,21 0,34 0,49 0,64 0,79 0,87 |
0,07 0,22 0,35 0,49 0,64 0,80 0,88 |
0,08 0,23 0,36 0,50 0,65 0,80 0,88 |
0,11 0,25 0,38 0,52 0,66 0,81 0,89 |
0,13 0,27 0,39 0,53 0,67 0,82 0,90 |
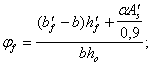
![]()
![]()
Найденные по формулам (263) и (264) значения ss в случае расположения арматуры в несколько рядов по высоте сечения умножаются на коэффициент dn.
4.10 (4.14). Ширина непродолжительного раскрытия трещин от действия всех нагрузок определяется как сумма ширины продолжительного раскрытия от действия постоянных и длительных нагрузок (при jl > 1,0) и приращения ширины раскрытия от действия кратковременных нагрузок (при jl = 1,0). Этому соответствует определение ширины непродолжительного раскрытия трещин по формуле
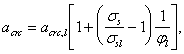 (265)
(265)
где acrс,l — ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок;
jl > 1,0— см. п. 4.7; если величина acrс,l определена с учетом формулы (253), то коэффициент jl в формуле (265) заменяется произведением jl jl1 (где jl1 ¾ см. п. 4.86);
ssl, ss — определяются согласно п. 4.9 соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.
Расчет по раскрытию трещин, наклонных к продольной оси элемента
4.11(4.17). Ширина раскрытия трещин, наклонных к продольной оси элемента, при армировании хомутами, нормальными к продольной оси, должна определяться по формуле
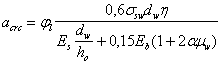 (266)
(266)
где jl ¾ коэффициент, принимаемый равным при учете:
кратковременных нагрузок и непродолжительного
действия постоянных и длительных нагрузок................. 1,00
продолжительного действия постоянных и длительных
нагрузок для конструкций из бетонов:
тяжелого:
естественной влажности............................................... 1,50
в водонасыщенном состоянии...................................... 1,20
при попеременном водонасыщении и высушивании... 1,75
мелкозернистого и легкого ¾ то же, что в формуле (249);
h ¾ то же, что в формуле (249);
dw ¾- диаметр хомутов;
![]()
ssw — напряжение в хомутах, определяемое по формуле
![]() ; (267)
; (267)
значение напряжения ssw не должно превышать Rs,ser;
Qb1 ¾ правая часть условия (72) с коэффициентом jb4, умноженным на 0,8,при этом, Rbt заменяется на значение Rbt,ser, принимаемое не более значения, соответствующего бетону класса В30;
Q — поперечная сила в конце наклонного сечения с проекцией длиной с.
Значение с принимается не более 2hо. Если при расчете элемента на действие равномерно распределенной нагрузки выполняется условие
![]() (268)
(268)
(где q1 ¾ см. п. 3.32), значение с можно принимать равным только 2hо.
Для элементов из легкого бетона класса В7,5 и ниже значение acrc, вычисленное по формуле (266), должно быть увеличено на 30 %.
При определении ширины непродолжительного раскрытия наклонных трещин от действия всех нагрузок должны учитываться указания п. 4.10. При этом в формуле (265) коэффициент jl назначается согласно настоящему пункту, а отношение ssl/ss заменяется на отношение напряжений sswl/ssw, определяемых по формуле (267) соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.
Допускается уменьшать величину асrc в 1,5 раза по сравнению с определенной по формуле (266), если элемент армирован продольными стержнями того же диаметра, что и хомуты, и с расстояниями по высоте сечения, равными шагу хомутов s.
Примеры расчета
Пример 53. Дано: железобетонная плита перекрытия с размерами поперечного сечения (для половины сечения плиты) по черт. 86: b = 85 мм, h = 400 мм, b¢f = 725 мм, h¢f= 50 мм; бетон тяжелый класса В25; рабочая арматура класса A-III (Rs = 365 МПа; Еs = 2×105 МПа), расположенная в два ряда (a1 = 58 мм; a2 = 33 мм); площадь ее сечения Аs = 760 мм2 (2Æ22) ; полный момент в середине пролета Мtot = 69 кН×м; все нагрузки постоянные и длительные; из расчета по прочности известно, что Ми = 92,3 кН×м и х = 30 мм.
Требуется произвести расчет по раскрытию трещин, нормальных к продольной оси элемента.
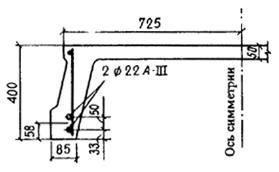
Черт. 86. К примеру расчета 53
Расчет.
ho
= h ¾ а = 400 ¾ 58 = 342 мм. Так как ![]() то, согласно п. 4.1,
принимаем, что элемент работает с трещинами в растянутой зоне.
то, согласно п. 4.1,
принимаем, что элемент работает с трещинами в растянутой зоне.
Для определения продолжительного раскрытия трещин вычислим напряжение в арматуре ss. Согласно формуле (263), величина ss на уровне центра тяжести арматуры равна:
![]()
Поскольку арматура расположена в два ряда, вычислим по формуле (262) коэффициент dn:
![]()
Напряжение в нижнем стержне арматуры равно:
ss = 273×1,08 = 294МПа.
Ширину
раскрытия трещин находим по формуле (249). Так как ![]() , значение
, значение ![]() принимаем равным 0,02.
Согласно п. 4.7, d = 1,0;
принимаем равным 0,02.
Согласно п. 4.7, d = 1,0; ![]() h = 1,0; d = 22 мм.
h = 1,0; d = 22 мм.
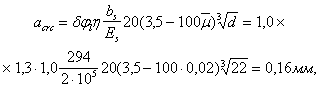
что меньше предельно допустимой ширины раскрытия трещин acrc2 = 0,3 мм.
Пример 54. Дано: железобетонная плита фундамента с размерами поперечного сечения h = 300 мм, b = 1150 мм; a = 42 мм; бетон тяжелый класса В15 (Rbt,ser = 1,15 МПа; Eb = 2,05×104 МПа); рабочая арматура класса A-III (Rs = 365 МПа; Еs = 2×105 МПа); площадь ее сечения Аs = 923 мм2 (6 Æ14); момент в расчетном сечении от постоянных и длительных нагрузок Ml = 63 кН×м, от кратковременных нагрузок Msh = 4 кН×м; предельный момент по прочности Мu = 80,5 кН×м; фундамент расположен выше уровня грунтовых вод.
Требуется произвести расчет по раскрытию нормальных трещин.
Расчет. ho = h ‑ а = 300 ‑ 42 = 258 мм. Определим необходимость вычисления ширины раскрытия трещин согласно п. 4.5. Для этого найдем момент трещинообразования Mcrc.
Так как ![]() момент Mcrc находим как для бетонного сечения,
используя формулу (246):
момент Mcrc находим как для бетонного сечения,
используя формулу (246):
Mcrc = Rbt,serWpl = 0,292bh2Rbt,ser = 0,292×1150×3002×1,15 = 34,75×106 Н×мм = 34,8 кН×м.
Так как Mr = Мtot = Ml + Мsh = 63 + 4 = 67 кН×м > Mcrc = 34,8 кН×м, проверка ширины раскрытия трещин необходима.
Поскольку
фундамент расположен выше уровня грунтовых вод, допустимая ширина
продолжительного раскрытия трещин, согласно табл. 1, поз. 4, acrc2 = 0,3 мм,
поэтому при ![]() согласно п. 4.6, расчет производим только на продолжительное раскрытие
трещин от действия момента Ml.
согласно п. 4.6, расчет производим только на продолжительное раскрытие
трещин от действия момента Ml.
Ширину раскрытия трещин определим по формуле (249).
Напряжение в арматуре ss вычислим по упрощенной формуле (263):
![]()
Коэффициенты,
вводимые в формулу (249), принимаем равными: d = 1,0; h
= 1,0; ![]() d = 14 мм,
тогда
d = 14 мм,
тогда
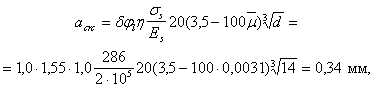
что больше допустимого значения acrc2 = 0,3 мм, в связи с чем целесообразно
произвести корректировку значения acrc
в меньшую сторону согласно п. 4.8б. Поскольку ![]() такая корректировка
допускается. Так как a2 = а = 42 мм < 0,2h = 0,2 × 300 = 60 мм, корректировка
значения acrc, согласно п. 4.8а, не производится.
такая корректировка
допускается. Так как a2 = а = 42 мм < 0,2h = 0,2 × 300 = 60 мм, корректировка
значения acrc, согласно п. 4.8а, не производится.
По формуле (256) определим значение Мо, предварительно вычислив:
![]()
![]()
Mo = Mcrс + ybh2Rbt,ser = 34,8×106 + 0,454×1150×3002×1,15 = 88,8×106 Н×мм = 88,8 кН×м.
Поскольку Мо = 88,8 кН×м > Mr = 67 кН×м, вычислим коэффициент jb по формуле (253) :
![]()
![]()
принимаем jl1 = 1;
jb = jf1jl1 = 0,79 < 1.
С учетом коэффициента jb, ширина раскрытия трещин равна acrc = 0,34×0,79 = 0,269 мм < 0,3 мм, т. е. меньше предельно допустимого значения.
Пример 55. Дано: железобетонная колонна промышленного здания с размерами поперечного сечения h = 500 мм, b = 400 мм; a = a¢ = 50 мм; бетон тяжелый класса В15 (Rb,ser = 11 МПа; Rbt,ser = 1,15 МПа; Eb = 2,05×104 МПа); рабочая арматура класса A-III (Еs = 2×105 МПа); площадь ее сечения As = A¢s = 1232 мм2 (2 Æ28); продольная сжимающая сила N = Nl = 500 кН; момент от полной нагрузки Mtot = 240 кН×м, в том числе момент от постоянных и длительных нагрузок Ml = 150 кН×м.
Требуется рассчитать колонну по раскрытию трещин.
Расчет. ho = h ‑ a =
500 ‑ 50 = 450 мм. Определим необходимость
расчета по раскрытию трещин. Для этого проверим условие (233). Так как ![]() то, согласно п. 4.2, момент
сопротивления Wpl находим как для
бетонного сечения. Используя формулу (246), находим
то, согласно п. 4.2, момент
сопротивления Wpl находим как для
бетонного сечения. Используя формулу (246), находим
Mcrc = 0,292bh2Rbt,ser = 0,292×400×5002×1,15 = 33,6×106 Н×мм.
Ядровое расстояние r определим по формуле (241). Для этого вычислим sb как для упругого тела (влиянием арматуры пренебрежем):
![]()
![]()
принимаем j = 0,7;
![]() .
.
По формуле (238) определим момент Mr:
![]()
т. е. условие (233) не выполняется. Следовательно, проверка раскрытия трещин обязательна.
Поскольку ![]() согласно п. 4,6
проверим непродолжительное раскрытие трещин. Для этого в соответствии с п. 4.10
предварительно вычислим ширину продолжительного раскрытия трещин от действия
усилий Ml и
Nl
по формуле (249). При этом воспользуемся упрощенной формулой (264) для ss.
согласно п. 4,6
проверим непродолжительное раскрытие трещин. Для этого в соответствии с п. 4.10
предварительно вычислим ширину продолжительного раскрытия трещин от действия
усилий Ml и
Nl
по формуле (249). При этом воспользуемся упрощенной формулой (264) для ss.
![]()
![]()
![]()
По вычисленным
значениям jf = 0,074, ma = 0,067 и ![]() находим по табл. 30 значение коэффициента jcrc = 0,33.
находим по табл. 30 значение коэффициента jcrc = 0,33.
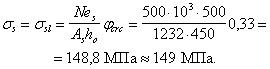
Согласно п.
4.7, s = 1,0; h = 1,00; ![]()
![]()
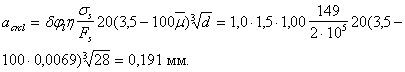
Напряжение в арматуре ss от действия всех нагрузок так же определим по формуле (264).
![]()
![]()
При jf = 0,074,ma
= 0,067 и ![]() коэффициент
jcrc согласно табл. 30 равен 0,522.
коэффициент
jcrc согласно табл. 30 равен 0,522.
![]()
Тогда, согласно формуле (265),
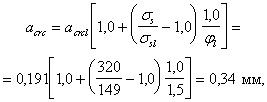
что меньше предельно допустимого значения acrcl = 0,4 мм (см. табл. 1, поз. 4).
Пример 56. Дано: свободно опертая балка перекрытия пролетом l = 5,5 м, нагруженная равномерно распределенными нагрузками: временной длительно действующей эквивалентной нагрузкой v = 30 кН/м и постоянной нагрузкой g = 12,5 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, hо = 370 мм; бетон тяжелый класса В 15 (Rbt,ser = 1,15 МПа; Eb = 2,05×104 МПа); хомуты двухветвевые из арматуры класса А-I (Еs = 2,1×105 МПа) с шагом s = 150 мм, диаметром 8 мм (4sw = 101 мм2).
Требуется произвести расчет по раскрытию наклонных трещин.
Расчет. Определим сначала необходимость расчета по раскрытию наклонных трещин, проверив условие (248).
Наибольшая поперечная сила в опорном сечении равна:
![]()
Согласно табл. 21, jb3 = 0,6.
jb3Rbt,serbho = 0,6×15×200×370 = 51060 H < Qmax = 117 кН,
т. е. наклонные трещины образуются и расчет по их раскрытию необходим.
Расчет производим согласно п. 4.11. Определим значения Q и Qb1.
q1 = g + v/2 = 12,5 + 30/2 = 27,5 кН/м;
jb4 = 1,5 (см. табл. 21).
Поскольку 0,2jb4Rbt,serb = 0,2×1,5×1,15×200 = 56,9 Н/мм > q1 = 27,5 Н/мм, значение с при определении Qb1 и Q принимаем равным с = 2h о = = 2×370 = 740 мм.
Отсюда
![]()
Q = Qmax ¾ q1s = 117 ¾ 27,5 0,740 = 96,65 кН .
Определим напряжение в хомутах по формуле (267):
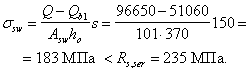
Согласно пп. 4.7 и 4.11, jl = 1,5; h = 1,3; dw = 8 мм.
![]()
![]()
Определим ширину раскрытия наклонных трещин по формуле (266):
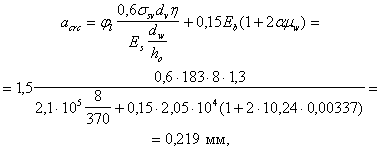
что меньше предельно допустимого значения асrc = 0,3 мм (см. табл. 1).
РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ
4.12(4.22) Деформации (прогибы, углы поворота) элементов железобетонных конструкций следует вычислять по формулам строительной механики, определяя входящие в них значения кривизны в соответствии с указаниями пп.4.13 — 4.21.
4.13(4.23). Кривизна определяется:
а) для участков элемента, где в растянутой зоне не образуются трещины, нормальные к продольной оси элемента (см. п. 4.1), ¾ как для сплошного тела;
б) для участков элемента, где в растянутой зоне имеются трещины, нормальные к продольной оси, — как отношение разности средних деформаций крайнего волокна сжатой зоны бетона и продольной растянутой арматуры к рабочей высоте сечения элемента.
При расчете по деформациям усилие от усадки бетона Nshr принимается равным нулю.
Определение кривизны железобетонных элементов на участках без трещин в растянутой зоне
4.14(4.24). На участках, где не образуются нормальные к продольной оси трещины, полная величина кривизны должна определяться по формуле
![]() (269)
(269)
где ![]() — кривизна
соответственно от кратковременных нагрузок (определяемых согласно указаниям п.
1.12) и от постоянных и длительных временных нагрузок, определяемая по
формулам:
— кривизна
соответственно от кратковременных нагрузок (определяемых согласно указаниям п.
1.12) и от постоянных и длительных временных нагрузок, определяемая по
формулам:
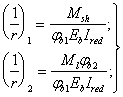 (270)
(270)
jb1 — коэффициент, учитывающий влияние кратковременной ползучести бетона и принимаемый для бетонов:
тяжелого, мелкозернистого и легкого при плотном
мелком заполнителе................................................... 0,85
легкого при пористом мелком заполнителе и
поризованного............................................................ 0,70
jb2 ¾ коэффициент, учитывающий влияние длительной ползучести бетона на деформации элемента без трещин и принимаемый по табл. 31.
Таблица 31 (34, 35)
|
|
Коэффициенты jb2 и vl при влажности воздуха окружающей среды, % |
|||||
|
Вид бетона |
40¾75 (нормальной) |
ниже 40 (пониженной) |
св. 75 (повышенной) |
|||
|
|
jb2 |
vl |
jb2 |
vl |
jb2 |
vl |
|
Тяжелый, легкий |
2,0 |
0,15 |
3,0 |
0,10 |
1,6 |
0,19 |
|
Поризованный |
2,0 |
0,07 |
3,0 |
0,04 |
1,6 |
0,09 |
|
Мелкозернистый |
|
|
|
|
|
|
|
групп: |
|
|
|
|
|
|
|
А |
2,6 |
0,10 |
3,9 |
0,07 |
2,1 |
0,125 |
|
Б |
3,0 |
0,08 |
4,5 |
0,05 |
2,4 |
0,10 |
|
В |
2,0 |
0,15 |
3,0 |
0,10 |
1,6 |
0,19 |
Примечания: 1. Влажность воздуха окружающей среды принимается согласно указаниям п. 1.8.
2. Группы мелкозернистого бетона см. п. 2.1.
3. При попеременном водонасыщении и высушивании бетона значения jb2, следует умножать, а значения vl ¾ делить на коэффициент 1,2.
Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне
4.15 (4.27). На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых, внецентренно сжатых, а также внецентренно растянутых при eо ³ 0,8ho элементов прямоугольного, таврового и двутаврового (коробчатого) сечений должна определяться по формуле
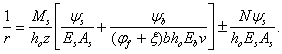 (271)
(271)
Для изгибаемых элементов последнее слагаемое правой части формулы (271) принимается равным нулю. Знак «минус» в этой формуле принимается при внецентренном сжатии, знак «плюс» — при внецентренном растяжении.
В формуле (271):
Мs — момент относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести площади сечения арматуры S, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, равный:
для изгибаемых элементов Мs = М;
для внецентренно сжатых и внецентренно растянутых элементов Мs = Nes;
z ¾ расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной (плечо внутренней пары сил), определяемое согласно указаниям п. 4.16;
ys — коэффициент, учитывающий работу растянутого бетона на участке с трещинами и определяемый согласно указаниям п. 4.17;
yb — коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами и принимаемый равным:
для тяжелого, мелкозернистого и легкого бетонов
класса В10 и выше ...............................................................0,9
для легкого и поризованного бетонов класса В7,5 и ниже... 0,7
jf ¾ коэффициент, определяемый по формуле (277);
x = x/ho — определяется согласно указаниям п. 4.16;
v ¾ коэффициент, характеризующий упруго-пластическое состояние бетона сжатой зоны и принимаемый равным:
при непродолжительном действии нагрузки ¾ коэффициенту vsh = 0,45;
при продолжительном действии нагрузки ¾ коэффициенту vl, определяемому по табл. 31.
Для изгибаемых и внецентренно сжатых элементов из тяжелого бетона при Mr < Mo кривизну допускается определять с учетом работы растянутого бетона над трещинами по формуле
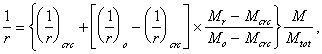 (272)
(272)
где
![]() (273)
(273)
![]() ¾ кривизна, определенная по
формуле (271) при моменте Мs,
¾ кривизна, определенная по
формуле (271) при моменте Мs,
равном:
для изгибаемых элементов Мs = Мo;
для внецентренно сжатых элементов Ms = Мo + Nуsr;
уsr = yo ‑а + r — расстояние от центра тяжести растянутой арматуры до оси, проходящей через наиболее удаленную ядровую точку (см. п. 4.2);
Мr — момент, определяемый согласно п. 4.2 от полной нагрузки, включающей постоянную, длительную и кратковременные нагрузки;
Мo ¾ момент, при котором растянутый бетон над трещинами выключается из работы, определяемый по формуле (256), в которой y уменьшается вдвое при учете продолжительного действия постоянных и длительных нагрузок;
Mcrc,r ¾ см. п. 4.2;
M, Mtot — моменты внешних сил относительно оси, проходящей через центр тяжести сечения, соответственно от рассматриваемой и от полной нагрузки;
jb1, jb2 — см. п. 4.14; при непродолжительном действии нагрузки jb2 = 1,0.
4.16(4.28). Значение x вычисляется по формуле
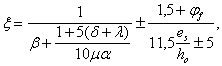 (274)
(274)
но принимается не более 1,0, при этом es/ho принимается не менее 0,5.
Для изгибаемых элементов последнее слагаемое правой части формулы (274) принимается равным нулю.
В формуле (274) верхние знаки принимаются при сжимающем, а нижние — при растягивающем усилии N.
В формуле (274):
b — коэффициент, принимаемый равным для бетона:
тяжелого и легкого................................................ 1,8
мелкозернистого.................................................... 1,6
поризованного........................................................ 1,4
![]() (275)
(275)
![]() (276)
(276)
 ; (277)
; (277)
![]() . (278)
. (278)
Значение z вычисляется по формуле
 (279)
(279)
Для элементов
прямоугольного сечения и таврового сечения с полкой в растянутой зоне в формулы
(276) ![]() и (279) вместо h¢f подставляются значения 2a' или h¢f = 0 соответственно при наличии или отсутствии
арматуры S¢.
и (279) вместо h¢f подставляются значения 2a' или h¢f = 0 соответственно при наличии или отсутствии
арматуры S¢.
Если ![]() , то для изгибаемых элементов при jf ³ jf1, где
, то для изгибаемых элементов при jf ³ jf1, где ![]() , значения z и
, значения z и ![]() — определяются при
— определяются при ![]() и jf = jf1,
а при jf < jf1, значения jf ,x, z и
и jf = jf1,
а при jf < jf1, значения jf ,x, z и ![]() — определяются без учета арматуры S¢.
Для внецентренно нагруженных элементов при
— определяются без учета арматуры S¢.
Для внецентренно нагруженных элементов при ![]() допускается всегда значения jf ,x, z и
допускается всегда значения jf ,x, z и
![]() определять без учета арматуры S¢.
определять без учета арматуры S¢.
Расчет
сечений, имеющих полку в сжатой зоне, при ![]()
производится
как прямоугольных шириной b¢f.
Расчетная ширина полки b¢f определяется согласно указаниям п. 3.23.
Для внецентренно сжатых элементов значение z должно приниматься не более 0,97es.
4.17 (4.29). Коэффициент ys определяется по формуле
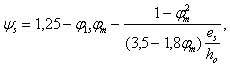 (280)
(280)
но не более 1,0, при этом следует принимать es/ho ³ 1,2/jls.
Для изгибаемых элементов последний член в правой части формулы (280) принимается равным нулю.
В формуле (280):
jls ¾ коэффициент, учитывающий влияние длительности действия нагрузки и принимаемый по табл. 32;
![]() (281)
(281)
Таблица 32(36)
|
Длительность действия |
Коэффициент jls при классе бетона |
|
|
нагрузки |
В 10 и выше |
В7,5 и ниже |
|
1. Непродолжительное действие при арматуре классов: |
|
|
|
А-II, А-III |
1,1 |
0,8 |
|
А-I, Вр-I |
1,0 |
0,7 |
|
2. Продолжительное действие |
0,8 |
0,6 |
но не более 1,0;
здесь Wpl ¾ см. п. 4.3;
Mr — см. п. 4.2.
4.18. Кривизна внецентренно растянутых элементов с продольной силой N, приложенной между центрами тяжести площадей арматуры S и S¢, на участках с нормальными трещинами в растянутой зоне определяется по формуле
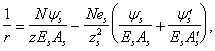 (282)
(282)
где zs = ho ‑ a¢ — расстояние между центрами тяжести площадей арматуры S и S';
ys, y¢s — коэффициенты, учитывающие работу растянутого бетона соответственно для арматуры S и S¢ и определяемые по формулам:
![]() (283)
(283)
![]() (284)
(284)
здесь jls ¾ коэффициент, принимаемый равным при действии нагрузки:
непродолжительном........................................... 0,70
продолжительном............................................... 0,35
Ncrc, N¢crc ¾ усилия, приложенные в той же точке, что и сила N, и соответствующие образованию трещин соответственно в более и менее растянутой зонах сечения; значения Ncrc и N¢crc определяются по формулам:
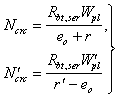 . (285)
. (285)
и принимаются не более N; кроме того, при r' < ео значение N¢crc принимается равным N.
В формулах (285):
Wpl, W¢pl ¾ значения Wpl, определенные согласно п. 4.3 соответственно для более и менее растянутой сторон сечения;
r, r¢ ¾ расстояния от центра тяжести приведенного сечения до ядровых точек, наиболее удаленных соответственно от более и менее растянутой сторон сечения; значения r и r¢ определяются по формуле (242).
4.19. Кривизна внецентренно растянутых
элементов с продольной силой N,
приложенной вне расстояния между центрами тяжести площадей арматуры S и S¢,
и при eо < 0,8hо
определяется линейной интерполяцией между кривизной ![]() , определенной по формуле (282) при еs = 0 (т.е. при eо = yso, где yso
— расстояние от центра тяжести площади арматуры S до центра тяжести приведенного сечения), и кривизной
, определенной по формуле (282) при еs = 0 (т.е. при eо = yso, где yso
— расстояние от центра тяжести площади арматуры S до центра тяжести приведенного сечения), и кривизной ![]() , определенной по формуле (271) еs
=0,8ho ‑ yso
(т.е. при ео = 0,8hо ‑ yso. Тогда значение кривизны равно:
, определенной по формуле (271) еs
=0,8ho ‑ yso
(т.е. при ео = 0,8hо ‑ yso. Тогда значение кривизны равно:
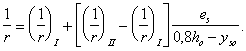 (286)
(286)
4.20. Для элементов прямоугольного сечения с симметричной арматурой, испытывающих косое внецентренное сжатие, кривизны вычисляются по формуле
![]() (287)
(287)
где ![]() — кривизна,
вычисленная как для плоского внецентренного сжатия согласно пп. 4.15-4.17 в
предположении действия силы N с
эксцентриситетом еo в плоскости оси симметрии сечения х, при этом принимается, что силовая
плоскость расположена между осью х и
диагональю сечения;
— кривизна,
вычисленная как для плоского внецентренного сжатия согласно пп. 4.15-4.17 в
предположении действия силы N с
эксцентриситетом еo в плоскости оси симметрии сечения х, при этом принимается, что силовая
плоскость расположена между осью х и
диагональю сечения;
jb — коэффициент, учитывающий влияние угла наклона силовой плоскости на величину деформаций кососжимаемых элементов и определяемый по формуле
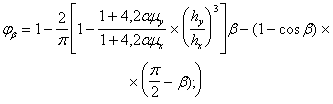 ; (288)
; (288)
![]()
здесь ![]()
![]() ¾
площади арматуры, расположенной у грани сечения, нормальной к осям
соответственно х и у, при этом угловой стержень учитывается
как при вычислении mх,
так и mу;
¾
площади арматуры, расположенной у грани сечения, нормальной к осям
соответственно х и у, при этом угловой стержень учитывается
как при вычислении mх,
так и mу;
hх, hy — размеры сечения в направлении осей соответственно х и у;
b — угол наклона силовой плоскости (плоскости эксцентриситета силы N) к плоскости оси х, рад.
Плоскость деформирования составляет с плоскостью оси х угол g, определяемый из равенства
![]() (289)
(289)
где Ix, Iy ¾ моменты инерции приведенного сечения относительно осей соответственное y и х.
Кривизны в плоскостях х и у при косом внецентренном сжатии равны:
![]() , (290)
, (290)
![]() (291)
(291)
где ![]() — определяется по формуле (287).
— определяется по формуле (287).
4.21 (4.30). Полная кривизна ![]() — для участка с трещинами в растянутой зоне должна определяться по формуле
— для участка с трещинами в растянутой зоне должна определяться по формуле
![]() (292)
(292)
где ![]() ¾
кривизна от непродолжительного действия всей нагрузки, на которую производится
расчет по деформациям согласно указаниям п.1.17;
¾
кривизна от непродолжительного действия всей нагрузки, на которую производится
расчет по деформациям согласно указаниям п.1.17;
![]() — кривизна от
непродолжительного действия постоянных и длительных нагрузок;
— кривизна от
непродолжительного действия постоянных и длительных нагрузок;
![]() — кривизна от
продолжительного действия постоянных и длительных нагрузок.
— кривизна от
продолжительного действия постоянных и длительных нагрузок.
Кривизны ![]() ,
, ![]() и
и ![]() определяются по
формулам (271), (272), (282), (286) и (287),
при этом
определяются по
формулам (271), (272), (282), (286) и (287),
при этом ![]() и
и ![]() вычисляются при значениях ys и v, отвечающих
непродолжительному действию
нагрузки, а
вычисляются при значениях ys и v, отвечающих
непродолжительному действию
нагрузки, а ![]() — при ys и v,
отвечающих продолжительному действию нагрузки. Если значения
— при ys и v,
отвечающих продолжительному действию нагрузки. Если значения ![]() и
и ![]() оказываются
отрицательными, они принимаются равными нулю.
оказываются
отрицательными, они принимаются равными нулю.
Определение прогибов
4.22 (4.31). Прогиб fm, обусловленный деформацией изгиба, определяется по формуле
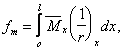 (293)
(293)
где ![]() —
изгибающий момент в сечении х от
действия единичной силы, приложенной по направлению искомого перемещения
элемента в сечении по длине пролета, для которого определяется, прогиб;
—
изгибающий момент в сечении х от
действия единичной силы, приложенной по направлению искомого перемещения
элемента в сечении по длине пролета, для которого определяется, прогиб;
![]() ¾
полная величина кривизны элемента в сечении х
от нагрузки, при которой определяется прогиб.
¾
полная величина кривизны элемента в сечении х
от нагрузки, при которой определяется прогиб.
При определении прогиба в середине пролета формула (293) может быть приведена к виду
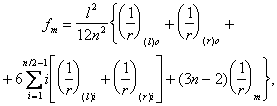 (294)
(294)
где ![]() ,
,![]() ¾
кривизны элемента соответственно на левой и правой опорах;
¾
кривизны элемента соответственно на левой и правой опорах;
![]() ,
, ![]() ,
, ![]() ¾
кривизны элемента в сечении i, в
симметричном сечении i' (черт. 87) и
в середине пролета;
¾
кривизны элемента в сечении i, в
симметричном сечении i' (черт. 87) и
в середине пролета;
п — четное число равных участков, на которое разделяется пролет элемента; число п рекомендуется принимать не менее 6.
Черт. 87. Эпюра кривизны в железобетонном элементе с переменным по длине сечением
В формулах
(293) и (294) кривизны ![]() определяются по формулам (269) и (292)
соответственно для участков без трещин и с трещинами; знак
определяются по формулам (269) и (292)
соответственно для участков без трещин и с трещинами; знак ![]() принимается в соответствии с эпюрой кривизн.
принимается в соответствии с эпюрой кривизн.
При определении прогибов статически неопределимых конструкций рекомендуется учитывать перераспределение моментов, вызванных образованием трещин и неупругими деформациями бетона.
Для изгибаемых элементов постоянного сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента (черт. 88).
Черт. 88. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения
а — схема расположения нагрузки; б — эпюра изгибающих моментов; в ¾ эпюра кривизны
4.23 (4.32, 4.33). Для
изгибаемых элементов при ![]() необходимо
учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб ftot равен сумме прогибов, обусловленных
соответственно деформацией изгиба fm и
деформацией сдвига fq.
необходимо
учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб ftot равен сумме прогибов, обусловленных
соответственно деформацией изгиба fm и
деформацией сдвига fq.
Прогиб fq, обусловленный деформацией сдвига, определяется по формуле 1
 (295)
(295)
где ![]() ¾ поперечная сила в
сечении х от действия по направлению
искомого перемещения единичной силы, приложенной в сечении, где определяется
прогиб;
¾ поперечная сила в
сечении х от действия по направлению
искомого перемещения единичной силы, приложенной в сечении, где определяется
прогиб;
gx ¾ деформация сдвига, определяемая по формуле
![]() (296)
(296)
здесь Qx ¾ поперечная сила в сечении х от действия внешней нагрузки;
jb2 ¾ коэффициент, учитывающий влияние длительной ползучести бетона и принимаемый по табл. 31; при непродолжительном действии нагрузки jb2 = 1,0;
G — модуль сдвига бетона (см. п. 2.12);
jcrc — коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:
на участках по длине элемента, где
отсутствуют нормальные и наклонные
к продольной оси элемента трещины.................... 1,0;
на участках, где имеются только наклонные к
продольной оси элемента трещины....................... 4,8;
на участках, где имеются только нормальные или нормальные и наклонные к продольной оси элемента трещины, — по формуле
![]() (297)
(297)
здесь Mx, ![]() — соответственно момент и кривизна в
сечении от нагрузки, при которой определяется прогиб, при непродолжительном ее
действии.
— соответственно момент и кривизна в
сечении от нагрузки, при которой определяется прогиб, при непродолжительном ее
действии.
4.24 (4.34). Для сплошных плит толщиной
менее 250 мм, армированных плоскими сетками, с трещинами в растянутой зоне
значения прогибов, подсчитанные по формуле (293), умножаются на коэффициент 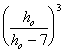 , принимаемый не более 1,5, где ho
— в мм.
, принимаемый не более 1,5, где ho
— в мм.
Определение продольных деформаций
4.25. Относительные деформации eo (удлинения или укорочения) в направлении продольной оси элементов определяются следующим образом.
1. Относительные деформации внецентренно сжатых и внецентренно растянутых элементов с однозначной эпюрой напряжений:
а) для внецентренно сжатых элементов или их отдельных участков — по формуле
![]() (298)
(298)
б) для внецентренно растянутых элементов или их участков при отсутствии трещин — по формуле
![]() (299)
(299)
В формулах (298) и (299) знак «плюс» соответствует деформациям укорочения, знак «минус» — деформациям удлинения;
в) для внецентренно растянутых элементов или их участков при наличии трещин (т. е. для элементов, указанных в п. 4.18), — по формуле
![]() (300)
(300)
где esm, e¢sm — средние величины удлинения арматуры соответственно S и S', определяемые по формулам:
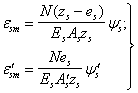 (301)
(301)
здесь zs, ys, y¢s ¾ см. п. 4.18.
2. Относительные деформации изгибаемых, внецентренно сжатых и внецентренно растянутых элементов с двухзначной эпюрой напряжений в сечении:
а) для элементов или их отдельных участков, не имеющих трещин в растянутой зоне, — по формуле
![]() . (302)
. (302)
Правило знаков то же, что для формул (298) и (299);
б) для участков элементов, указанных в п. 4.15, имеющих трещины в растянутой зоне, — по формуле
![]() (303)
(303)
где esm, ebm — средние величины соответственно относительного удлинения арматуры и относительного укорочения крайнего сжатого волокна бетона на участке между трещинами, определяемые по формулам:
![]() (304)
(304)
![]() (305)
(305)
где Ms, ys, z, jf, x ¾ см. пп. 4.15 — 4.17; правило знаков — см. п. 4.15;
в) для участков внецентренно растянутых элементов, указанных в п. 4.19, — линейной интерполяцией между значением eо, определенным по формуле (300) при еs = 0 (т. е. при еo = yso), и значением еo, определенным по формуле (303) при еs = 0,8ho (т. е. при при еo = 0,8 ho + yso), где yso ¾ см. п. 4.19.
В формулах (298) ¾ (305):
yso — расстояние от рассматриваемого волокна до центра тяжести арматуры S;
уо — то же, до центра тяжести приведенного сечения;
jb1, jb2 — см. п. 4.14; при непродолжительном действии нагрузки jb2 = 1,0;
v — см. п. 4.15.
Деформации eо, определенные по формулам (298) — (303), со знаком «плюс» отвечают укорочению, со знаком «минус» — удлинению.
При одновременном действии постоянных, длительных и кратковременных нагрузок порядок вычисления eо аналогичен определению полной кривизны по п. 4.21.
4.26. Укорочение (удлинение) элементов на уровне рассматриваемого волокна определяется по формуле
![]() (306)
(306)
где eоi ¾ относительные продольные деформации в сечении, расположенном посредине участка длиной li;
п — число участков, на которые разбивается длина элемента.
Приближенные методы расчета деформаций
4.27. Прогибы железобетонных изгибаемых элементов из тяжелого бетона постоянного сечения, эксплуатируемых при нормальной и повышенной влажности (влажность воздуха окружающей среды свыше 40 %), заведомо меньше предельно допустимых, если выполняется условие
![]() (307)
(307)
где llim — граничное отношение пролета к рабочей высоте сечения, менее которого проверка прогибов не требуется (табл. 33).
При ![]() прогибы заведомо
меньше предельно допустимых, если выполняется условие (308), учитывающее
влияние деформаций сдвига на прогиб элемента:
прогибы заведомо
меньше предельно допустимых, если выполняется условие (308), учитывающее
влияние деформаций сдвига на прогиб элемента:
![]() (308)
(308)
Значения llim, приведенные в
табл. 33, отвечают продолжительному действию равномерно распределенной нагрузки
на свободно опертую балку при предельном прогибе, равном ![]() .
.
Таблица 33
|
Сечения |
Коэффициенты jf, jft |
Значения llim для определения случаев, когда проверка прогибов элементов из тяжелого бетона не требуется, при значениях ma, равных |
|
||||||||
|
|
|
0,02 |
0,04 |
0,07 |
0,10 |
0,15 |
0,20 |
0,30 |
0,40 |
0,50 |
|
|
|
jf = jft = 0 |
25 17 |
17 12 |
14 10 |
12 9 |
10 8 |
9 8 |
10 10 |
11 11 |
11 11 |
|
|
|
jf = 0,2; jft = 0 |
31 22 |
22 16 |
18 13 |
16 11 |
12 9 |
10 8 |
10 10 |
11 11 |
11 11 |
|
|
|
jf = 0,4; jft = 0 |
42 25 |
25 17 |
23 15. |
18 12 |
14 10 |
11 8 |
10 9 |
10 9 |
11 11 |
|
|
|
jf = 0,6; jft = 0 |
45 30 |
28 30 |
24 17 |
19 14 |
16 12 |
13 9 |
11 9 |
10 10 |
11 11 |
|
|
|
jf = 0,8; jft = 0 |
48 32 |
30 21 |
25 18 |
20 15 |
18 13 |
15 10 |
12 9 |
10 9 |
10 10 |
|
|
|
jf = 1,0; jft = 0 |
50 35 |
33 22 |
26 19 |
23 17 |
20 14 |
17 12 |
14 9 |
11 9 |
10 10 |
|
|
|
jft = 0,2; jf = 0 |
28 18 |
17 12 |
14 10 |
12 9 |
10 8 |
9 8 |
10 10 |
11 11 |
11 11 |
|
|
|
jft = 0,6; jf = 0 |
32 20 |
20 13 |
15 10 |
13 9 |
10 8 |
9 9 |
10 10 |
11 11 |
12 12 |
|
|
|
jft = 1,0; jf = 0 |
36 22 |
23 14 |
16 10 |
13 9 |
10 8 |
9 9 |
10 10 |
11 11 |
12 12 |
|
|
|
jf = jft = 0,2 |
34 23 |
25 17 |
19 14 |
16 11 |
12 9 |
10 8 |
10 10 |
11 11 |
11 11 |
|
|
|
jf = jft = 0,6 |
48 33 |
34 25 |
26 18 |
21 14 |
16 12 |
15 9 |
11 8 |
10 10 |
11 11 |
|
|
|
jf = jft = 1,0 |
55 42 |
44 36 |
36 21 |
26 17 |
20 14 |
17 12 |
14 9 |
11 9 |
10 9 |
|
|
As = A¢s |
|
||||||||||
Примечание. Значения llim, приведенные над чертой, применяются при расчете элементов, армированных сталью класса А-II, под чертой ¾ класса A-III.
Если
предельно допустимые прогибы f (см. п. 1.17) меньше ![]() , значения llim табл. 33 должны
быть уменьшены в
, значения llim табл. 33 должны
быть уменьшены в ![]() раз (например, при
раз (например, при ![]() —
в 1,5 раза, при
—
в 1,5 раза, при ![]() — в
2 раза).
— в
2 раза).
Для сплошных плит толщиной менее 250 мм, армированных плоскими сетками, значения llim уменьшаются делением на коэффициент, указанный в п. 4.24.
Примечание. Значения llim могут быть увеличены в следующих случаях:
а) если прогиб определяется от действия момента Ml, составляющего часть полного момента Мtot (поз. 2 ¾ 4 табл. 2), ¾ умножением llim табл. 33 на отношение Мtot/ Ml;
б) если
нагрузка отличается от равномерно распределенной ¾ умножением значений llim табл. 33 на
отношение ![]() где рm ¾ коэффициент,
принимаемый по табл. 35 в зависимости от схемы загружения;
где рm ¾ коэффициент,
принимаемый по табл. 35 в зависимости от схемы загружения;
в) если прогиб определяется от совместного действия кратковременных, длительных и постоянных нагрузок — умножением значений llim табл. 33 на коэффициент jq, определяемый по формуле
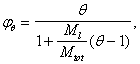
где q ¾ отношение деформации от длительного действия нагрузки к деформации от кратковременного действия той же нагрузки, принимаемое равным для элементов: прямоугольного сечения q = 1,8; таврового сечения с полкой в сжатой зоне q = 1,5; таврового сечения с полкой в растянутой зоне q = 2,2.
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ
4.28. Для изгибаемых элементов из
тяжелого бетона постоянного сечения, указанных в п. 4.15 и эксплуатируемых при
влажности воздуха окружающей среды свыше 40 %, кривизна ![]() на участках с
трещинами определяется по формуле
на участках с
трещинами определяется по формуле
![]() (309)
(309)
где j1, j2 — см. табл. 34.
При
одновременном действии постоянных, длительных и кратковременных нагрузок
кривизна ![]() определяется по
формуле
определяется по
формуле
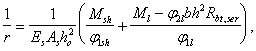 (310)
(310)
где j1sh — коэффициент j1 при непродолжительном действии нагрузки;
j1l, j2l — коэффициенты j1 и j2 при продолжительном действии нагрузки.
ОПРЕДЕЛЕНИЕ ПРОГИБОВ
4.29. Для изгибаемых элементов при ![]() прогиб f определяется следующим
образом:
прогиб f определяется следующим
образом:
а) для элементов постоянного сечения, работающих как свободно опертые или консольные балки, ¾ по формуле
![]() (311)
(311)
где ![]() ¾
кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб;
¾
кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб;
рm — коэффициент, принимаемый по табл. 35;
Таблица 34
|
Коэффициенты |
Коэффициент j1 при значениях ma, равных |
Коэффициент j2 при значениях ma, равных |
||||||||||||||||||||||
|
jft |
jf |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,10 |
0,13 |
0,15 |
0,17 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
<0,04 |
0,04-0,08 |
0,08-0,15 |
0,15-0,30 |
0,30-0,50 |
|
Продолжительное действие нагрузки |
||||||||||||||||||||||||
|
0,0 0,0 0,0 0,0 0,0 0,0 |
0,0 0,2 0,4 0,6 0,8 1,0 |
0,43 0,49 0,52 0,54 0,56 0,57 |
0,39 0,46 0,49 0,51 0,53 0,54 |
0,36 0,44 0,47 0,49 0,51 0,52 |
0,34 0,42 0,46 0,48 0,49 0,51 |
0,32 0,41 0,45 0,47 0,48 0,50 |
0,30 0,39 0,44 0,46 0,47 0,49 |
0,28 0,37 0,42 0,44 0,46 0,48 |
0,26 0,35 0,40 0,43 0,45 0,47 |
0,23 0,31 0,38 0,42 0,44 0,46 |
0,22 0,29 0,35 0,39 0,42 0,44 |
0,21 0,27 0,33 0,37 0,40 0,42 |
0,19 0,25 0,31 0,35 0,38 0,41 |
0,16 0,21 0,26 0,31 0,35 0,38 |
0,14 0,19 0,24 0,28 0,32 0,35 |
0,13 0,17 0,22 0,25 0,29 0,32 |
0,12 0,16 0,20 0,23 0,27 0,30 |
0,11 0,14 0,18 0,22 0,25 0,28 |
0,10 0,13 0,17 0,20 0,23 0,26 |
0,10 0,12 0,13 0,13 0,14 0,15 |
0,07 0,09 0,10 0,11 0,12 0,13 |
0,04 0,05 0,06 0,08 0,09 0,10 |
0,00 0,00 0,02 0,02 0,04 0,06 |
0,00 0,00 0,00 0,00 0,00 0,00 |
|
0,2 0,4 0,6 0,8 1,0 |
0,0 0,0 0,0 0,0 0,0 |
0,47 |
0,40 0,42 0,43
|
0,36 0,36 0,37 0,38 0,40 |
0,33 0,33 0,33 0,33 0;33 |
0,31 0,31 0,31 0,30 0,30 |
0,30 0,30 0,30 0,29 0,29 |
0,28 0,28 0,27 0,27 0,27 |
0,26 0,26 0,25 0,24 0,24 |
0,23 0,22 0,22 0,22 0,22 |
0,22 0,21 0,21 0,21 0,20 |
0,21 0,20 0,20 0,20 0,19 |
0,19 0,19 0,18 0,17 0,17 |
0,16 0,16 0,15 0,15 0,15 |
0,14 0,14 0,14 0,14 0,14 |
0,13 0,13 0,12 0,12 0,12 |
0,11 0,11 0,11 0,11 0,11 |
0,11 0,10 0,10 0,10 0,10 |
0,10 0,10 0,10 0,10 0,10 |
0,15 0,18 0,20 0,23 0,25 |
0,12 0,16 0,19 0,22 0,24 |
0,08 0,13 0,17 0,20 0,23 |
0,03 0,06 0,09 0,12 0,14 |
0,00 0,02 0,03 0,05 0,06 |
|
0,2 0,4 0,6 0,8 1,0 |
0,2 0,4 0,6 0,8 1,0 |
0,51 |
0,45 0,53 |
0,43 0,49 0,53 |
0,40 0,47 0,50 0,53 0,61 |
0,38 0,45 0,48 0,50 0,53 |
0,37 0,43 0,46 0,48 0,50 |
0,36 0,42 0,44 0,46 0,48 |
0,34 0,39 0,41 0,44 0,45 |
0,30 0,37 0,39 0,41 0,43 |
0,28 0,35 0,38 0,39 0,40 |
0,26 0,33 0,36 0,38 0,39 |
0,24 0,30 0,34 0,37 0,38 |
0,21 0,26 0,31 0,34 0,36 |
0,19 0,23 0,28 0,31 0,34 |
0,17 0,21 0,25 0,29 0,32 |
0,16 0,20 0,23 0,26 0,29 |
0,14 0,18 0,21 0,25 0,27 |
0,13 0,17 0,20 0,23 0,26 |
0,16 0,20 0,24 |
0,13 0,19 0,22 0,25 0,26 |
0,08 0,14 0,20 0,24 0,25 |
0,04 0,07 0,12 0,19 0,20 |
0,00 0,03 0,04 0,08 0,12 |
|
Непродолжительное действие нагрузки |
||||||||||||||||||||||||
|
0,0 0,0 0,0 0,0 0,0 0,0 |
0,0 0,2 0,4 0,6 0,8 1,0 |
0,64 0,72 0,76 0,79 0,82 0,84 |
0,59 0,66 0,69 0,71 0,73 0,74 |
0,56 0,63 0,66 0,69 0,70 0,71 |
0,53 0,61 0,65 0,67 0,68 0,69 |
0,51 0,59 0,63 0,65 0,67 0,68 |
0,50 0,58 0,62 0,64 0,66 0,67 |
0,49 0,57 0,61 0,63 0,65 0,66 |
0,46 0,56 0,60 0,63 0,65 0,66 |
0,43 0,53 0,59 0,62 0,64 0,66 |
0,41 0,51 0,57 0,61 0,63 0,65 |
0,40 0,49 0,56 0,60 0,63 0,65 |
0,37 0,46 0,53 0,58 0,61 0,63 |
0,34 0,43 0,49 0,55 0,58 0,61 |
0,32 0,40 0,46 0,52 0,56 0,59 |
0,30 0,37 0,44 0,49 0,53 0,56 |
0,28 0,35 0,41 0,46 0,50 0,54 |
0,26 0,33 0,39 0,44 0,48 0,52 |
0,25 0,31 0,37 0,42 0,46 0,50 |
0,17 0,21 0,23 0,25 0,26 0,27 |
0,14 0,18 0,20 0,21 0,23 0,24 |
0,09 0,11 0,14 0,16 0,17 0,18, |
0,02 0,03 0,04 0,05 0,06 0,07 |
0,00 0,00 0,00-0,00 0,00 0,00 |
|
0,2 0,4 0,6 0,8 1,0 |
0,0 0,0 0,0 0,0 0,0 |
0,74 |
0,60 0,63 0,81 |
0,56 0,57 0,59 0,63 0,84 |
0,53 0,54 0,54 0,55 0,57 |
0,51 0,51 0,51 0,51 0,52 |
0,49 0,49 0,49 0,49 0,49 |
0,47 0,47 0,47 0,47 0,47 |
0,44 0,44 0,44 0,44 0,44 |
0,42 0,42 0,42 0,42 0,42 |
0,40 0,40 0,40 0,40 0,40 |
0,39 0,39 0,39 0,39 0,39 |
0,37 О,Э7 0,37 0,37 0,37 |
0,34 0,34 0,34 0,34 0,34 |
0,32 0,32 0,32 0,32 0,32 |
0,30 0,30 0,30 0,30 0,30 |
0,28 0,28 0,28 0,28 0,28 |
0,26 0,26 0,26 0,26 0,27 |
0,25 0,25 0,25 0,25 0,25 |
0,28 0,35 0,36 0,45 0,50 |
0,23 0,31 0,39 0,40 0,46 |
0,16 0,25 0,32 0,38 0,44 |
0,07 0,14 0,20 0,25 0,29 |
0,00 0,03 0,08 0,12 0,15 |
|
0,2 0,4 0,6 0,8 1,0 |
0,2 0,4 0,6 0,8 1,0 |
0,79 |
0,67 0,77 |
0,63 0,69 0,76 |
0,61 0,66 0,70 0,76 0,92 |
0,59 0,64 0,67 0,71 0,76 |
0,58 0,62 0,65 0,68 0,71 |
0,56 0,61 0,64 0,66 0,69 |
0,55 0,58 0,61 0,64 0,66 |
0,52 0,56 0,58 0,61 0,63 |
0,50 0,55 0,57 0,59 0,61 |
0,48 0,54 0,56 0,58 0,60 |
0,46 0,52 0,55 0,57 0,58 |
0,42 0,48 0,53 0,56 0,57 |
0,39 0,45 0,50 0,53 0,56 |
0,37 0,43 0,47 0,51 0,54 |
0,35 0,40 0,45 0,49 0,52 |
0,33 0,38 0,43 0,47 0,50 |
0,31 0,37 0,41 0,45 0,48 |
0,27 0,39 0,50 |
0,24 0,37 0,46 0,60 0,72 |
0,17 0,30 0,44 0,57 0,70 |
0,08 0,16 0,28 0,41 0,55 |
0,00 0,04 0,11 0,21 0,31 |
![]()
![]()
![]()
при схеме загружения свободно опертой или консольной балки, не приведенной в табл. 35, прогиб определяется по формулам сопротивления материалов при жесткости, равной отношению наибольшего момента к наибольшей кривизне;
б) если прогиб, определенный по подпункту «а», превышает допустимый, то для слабоармированных элементов (m £ 0,5 %) его значение рекомендуется уточнять за счет учета повышенной жесткости на участках без трещин при переменной жесткости на участке с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле
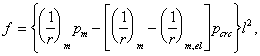 (312)
(312)
где рcrc — коэффициент, принимаемый по табл. 36 в зависимости от отношения Mcrc/Mtot (Mcrc ¾ см. пп. 4.2 и 4.3) ;
![]() — кривизна в сечении с
наибольшим моментом, определенная как для сплошного тела по формуле (270), от
нагрузки, при которой определяется прогиб; допускается значение Ired в формуле (270) определять как для бетонного элемента.
— кривизна в сечении с
наибольшим моментом, определенная как для сплошного тела по формуле (270), от
нагрузки, при которой определяется прогиб; допускается значение Ired в формуле (270) определять как для бетонного элемента.
Для иных схем загружения величина f может быть определена по формуле (314) ;
в) для изгибаемых элементов с защемленными опорами прогиб в середине пролета определяется по формуле
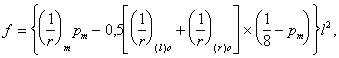 (313)
(313)
где ![]() — кривизны элемента соответственно в
середине пролета, на левой и правой опорах;
— кривизны элемента соответственно в
середине пролета, на левой и правой опорах;
рm ¾ коэффициент, определяемый по табл. 35 как для свободно опертой балки;
г) для элементов переменного сечения, а также в тех случаях, когда требуется более точное, чем по формулам (311) и (313), определение прогибов, а сами элементы и нагрузка симметричны относительно середины пролета, прогиб определяется по формуле
Таблица 35
|
Схема загружения консольной балки |
Коэффициент Рт |
Схема загружения свободно опертой балки |
Коэффициент Рт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание. При загружении элемента
одновременно по нескольким схемам ![]() (где pm1 и M1,
pm2 и M2
и т. д. ¾
соответственно коэффициент pm, и
наибольший изгибающий момент М для
каждой схемы загружения). В этом случае в формулах (311) ¾
(313) величина
(где pm1 и M1,
pm2 и M2
и т. д. ¾
соответственно коэффициент pm, и
наибольший изгибающий момент М для
каждой схемы загружения). В этом случае в формулах (311) ¾
(313) величина ![]() определяется при
значении М, равном сумме наибольших изгибающих моментов, определенных для
каждой схемы загружения.
определяется при
значении М, равном сумме наибольших изгибающих моментов, определенных для
каждой схемы загружения.
Таблица 36
|
Mcrc/Mtot |
1,00 |
0,99 |
0,98 |
0,96 |
0,94 |
0,92 |
0,90 |
0,85 |
0,80 |
|
Pcrc |
0,104 |
0,088 |
0,082 |
0,073 |
0,067 |
0,062 |
0,058 |
0,049 |
0,042 |
Продолжение табл. 36
|
Mcrc/Mtot |
0,75 |
0,70 |
0,60 |
0,50 |